Wikipédia:Sélection/Géométrie
Variété (géométrie) Une variété est un espace topologique abstrait, construit par recollement d'autres espaces simples. Comme les enfants s'amusent à construire avec du papier des tétraèdres, des cubes et autres polyèdres en dessinant la figure d'un patron sur une feuille blanche, en découpant convenablement les bords, en pliant et en recollant, les mathématiciens obtiennent un cercle en repliant un segment sur lui-même, un cylindre ou un cône en repliant une bande plane sur elle-même. Un autre exemple classique est le ruban de Möbius illustré ci-contre (en toute rigueur exemple de variété à bord). Il est également possible de rajouter des anses à une sphère. Parmi les variétés les plus simples figurent les courbes et surfaces du plan et de l'espace euclidien. Traditionnellement définies par des équations, elles s'obtiennent toutes, au même titre que les polyèdres, à partir d'un « patron » plan et d’« instructions de collage ». C'est là le mode de définition général des variétés. |
Géométrie projective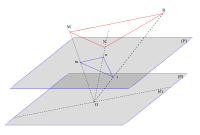 La géométrie projective est une branche des mathématiques qui étudie les notions de perspective et d'horizon. Elle permet de simplifier des théorèmes de géométrie plane comme le théorème de Pappus : le calcul barycentrique est légitimé dans les coordonnées barycentriques. Lire l’article |
Polytope régulier Un polytope régulier est une figure de géométrie présentant un grand nombre de symétries ; sa définition précise a varié suivant les époques. Parmi les polytopes réguliers, on trouve les carrés, les pentagones réguliers, les solides de Platon, ...
|
Théorème de Thalès Le théorème de Thalès est un théorème de géométrie, attribué selon la légende au mathématicien et philosophe grec Thalès de Milet ; en réalité Thalès s'est davantage intéressé aux angles opposés dans des droites sécantes, aux triangles isocèles et aux cercles circonscrits. Cette propriété de proportionnalité était connue des Babyloniens. Mais la première démonstration de ce théorème est attribuée à Euclide qui la présente dans ses Éléments (proposition 2 du livre VI) : il le démontre par proportionnalité d'aires de triangles de hauteur égale. Selon la légende, une application a été de calculer la hauteur des pyramides d'Égypte en mesurant la longueur de l'ombre au sol de chaque pyramide, et la longueur de l'ombre d'un bâton de hauteur donnée. |
RotationUne rotation est un élément du groupe SO(3).
|
Pavage Un pavage est un recouvrement d'un espace par des fermés d'intérieurs disjoints. On demande souvent au pavage d'être régulier, de présenter suffisamment de symétries. Il y a 17 pavages réguliers du plan euclidien. Le pavage de Penrose est bien connu.
|