Limaçon de Pascal

Le limaçon de Pascal est une courbe plane fermée présentant éventuellement un point double, obtenue en traçant le mouvement décrit par un point d'un disque roulant (sans glisser) sur un cercle. La cardioïde en est un cas particulier : le point double dégénère alors un rebroussement de première espèce. Le limaçon trisecteur est un second cas particulier (à ne pas confondre avec la trisectrice de Maclaurin)

Le limaçon est une épitrochoïde, c'est-à-dire une trochoïde avec un cercle pour base du mouvement.
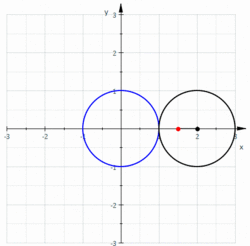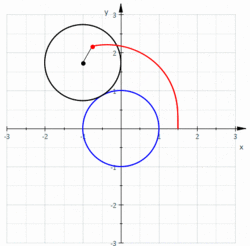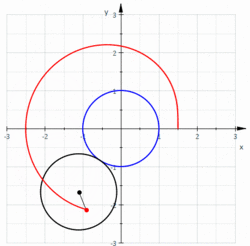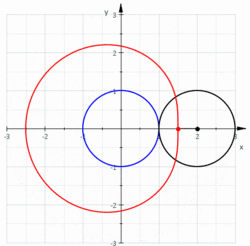
La courbe a pour équation complexe $z=2r\mathrm {e} ^{it}-d\mathrm {e} ^{i2t}$ où $r$ est le rayon des deux cercles et $d$ la distance séparant le point mobile du centre du second cercle.

Les limaçons de Pascal sont aussi les podaires d'un cercle par rapport à un point quelconque.

Équations

Le limaçon a pour équation en coordonnées polaires :

$r=a+b\cos \theta ~$

Pour cette équation, le cercle porteur a pour rayon a/2 et pour centre le point de coordonnées polaires (b/2;0). Le point mobile est à une distance b/2 du centre du cercle mobile.

Elle a pour équation complexe:

$z={\frac {b}{2}}+a\mathrm {e} ^{i\theta }+{\frac {b}{2}}\mathrm {e} ^{2i\theta }$

Le point $B(b/2,)$ est le foyer singulier du limaçon, intersection des asymptotes complexes.

En coordonnées cartésiennes, l'équation devient :

$(x^{2}+y^{2})^{2}-(a^{2}+2bx)(x^{2}+y^{2})+b^{2}x^{2}=0.~$

C'est donc une quartique rationnelle, c'est-à-dire une courbe algébrique de degré 4 .

En tant que quartique unicursale, elle possède une paramétrisation rationnelle:

$\left\{{\begin{aligned}x(t)&=(1-t^{2}){\frac {a+b+(a-b)t^{2}}{(1+t^{2})^{2}}}\\y(t)&=2t{\frac {a+b+(a-b)t^{2}}{(1+t^{2})^{2}}}\end{aligned}}\right.,\,t\in ]-\infty ;+\infty ]$

Histoire

Planche 40 de Underweysung des Messung de Dürer (1538) - Limaçon à point double construit comme une épitrochoïde.

La courbe est étudiée par Gilles Personne de Roberval vers 1640-1650 dans son Observations sur la composition des mouvements et le moyen de trouver les touchantes des lignes courbes où il en construit les tangentes, puis dans son Traité des indivisibles quand il en calcule l'aire inscrite. Il la mentionne sous le nom de «Limaçon de M. Paschal», en référence à Étienne Pascal, père de Blaise Pascal.

L'intérêt des Pascal pour les roulettes est bien documenté. Le limaçon, qui en est une généralisation, a été proposé vers 1630 comme sujet d'étude par Étienne Pascal, père de Blaise Pascal, au père Mersenne^{[réf. nécessaire]}. Étienne Pascal l'utilise dans le cas de la trisection de l'angle et il est probable que ce soit la motivation de sa construction.

Cependant l'étude de cette courbe est probablement antérieure puisqu'on la trouve déjà chez Dürer dans son Underweysung der Messung (Instructions pour la mesure à la règle et au compas) dont la première publication date de 1525. Dürer en indique le tracé avec des outils de dessin et lui donne le nom de ligne araignée (en allemand, Spinnen Lini et en latin aranei linea).

Allure générale

Selon les valeurs de b/a, l'allure de la courbe change :

• si b/a < 1, le limaçon est dit elliptique, c'est l'inverse d'une ellipse par rapport à un de ses foyers. La forme ressemble à un cercle déformé pour b/a<1/2, pour b/a=1/2, la courbe possède un méplat et pour 1/2 < b/a < 1, la courbe ressemble à un haricot;
• si b/a = 1 la courbe est une cardioïde;
• si b/a > 1, le limaçon est dit hyperbolique, c'est l'inverse d'une hyperbole par rapport à un de ses foyers. La courbe possède une boucle. Le cas b/a = 2 conduit à une courbe trisectrice.

Cas b/a = 0.5 : le limaçon a un méplat

Cas b/a = 1 : le limaçon est une cardioïde

Cas b/a = 2 : le limaçon est une courbe trisectrice

Propriétés différentielles

L'équation de la tangente au point de coordonnées polaires $(\rho ;\theta )$ est

$(a\cos \theta +b\cos 2\theta )x+(a\sin \theta +b\sin 2\theta )y=\rho ^{2}.$

Le rayon de courbure est:

$R={\frac {(b^{2}+2ab\cos \theta +a^{2})^{\frac {3}{2}}}{2b^{2}+3ab\cos \theta +a^{2}}}$

Pour ${\frac {a}{2}}<b<a$ la courbe possède deux points d'inflexion pour $\theta =\pm \arccos \left(-{\frac {2b^{2}+a^{2}}{3ab}}\right)$ et $\rho ={\frac {2(a^{2}-b^{2})}{3a}}$.

Ces points deviennent des points d'ondulation si $b={\frac {a}{2}}$

Si $b\neq a$, la longueur d'un arc de limaçon entre $M(0)$ et $M(\theta )$ nécessite l'utilisation d'une intégrale elliptique de deuxième espèce:

$L(\theta )=2(a+b)\int _{0}^{\theta /2}{\sqrt {1-{\frac {4ab}{(a+b)^{2}}}\sin ^{2}\varphi }}\,\mathrm {d} \varphi .$

L'aire balayée par le vecteur ${\overrightarrow {OM}}(\theta )$ pour $\theta$ variant de 0 à $\theta _{1}$ est :

$A(\theta _{1})={\frac {2a^{2}+b^{2}}{4}}\theta _{1}+{\frac {b^{2}}{8}}\sin 2\theta _{1}+ab\sin \theta _{1}.$

En particulier, l'aire d'un limaçon sans boucle (cas où $b\leq a$ est :

$A=\left(a^{2}+{\frac {b^{2}}{2}}\right)\pi .$

Autres systèmes de construction

Podaire

Le limaçon d'équation $r=a+b\cos \theta ~$ est la podaire du cercle de centre $B(b;0)$ et de rayon $a$ par rapport à l'origine $O$ du repère.

En effet dans l'image ci-dessous on considère le projeté de O sur la tangente au cercle en T. Les coordonnées polaires de ${\overrightarrow {HM}}={\overrightarrow {BT}}$ sont $(a;\theta )$ et celles de ${\overrightarrow {OH}}$ sont $(b\cos \theta ;\theta )$. Celles de M sont donc $(a+b\cos \theta ;\theta )$ pour $\theta$ variant de 0 à $2\pi$. Ce qui correspond à l'équation polaire du limaçon.

Limaçon de Pascal comme podaire d'un cercle

Limaçon de Pascal comme podaire d'un cercle- Animation

Conchoïde

Ce même limaçon est la conchoïde du cercle de diamètre OB où B a pour coordonnées polaires $(b;0)$, de pôle O et de module $a$.

En effet par un raisonnement analogue au précédent, pour $\theta \in [-\pi /2,\pi /2]$, on a $M_{1}(a+b\cos \theta ;\theta )$ et $M_{2}(b\cos \theta -a;\theta )$. Or le point $M_{2}$ est confondu avec $N(a+b\cos(\theta +\pi );\theta +\pi )$. Le point $M_{1}$ parcourt une première partie du limaçon, tandis que $M_{2}$ en parcourt l'autre partie.

Limaçon de Pascal comme conchoïde

Limaçon de Pascal comme conchoïde - Animation

Inverse de conique

L'équation polaire d'un conique par rapport à un de ses foyers et suivant l'axe focal est $\rho ={\frac {p}{1+e\cos(\theta )}}$.

Le limaçon d'équation polaire $r=a+b\cos \theta ~$ est donc la courbe inverse de la conique de foyer O, de même axe principal, de paramètre $1/a$ et d’excentricité $b/a$ par rapport au cercle unité.

Enveloppe de cercles

Le limaçon est l'enveloppe de tous les cercles passant par un point fixe (O) et dont le centre est sur un cercle donné.

Le limaçon d'équation polaire $r=a+b\cos \theta ~$ est l'enveloppe des cercles passant par O et dont les centres sont sur le cercle de centre B(b;0) et de rayon a.

Limaçon de Pascal comme enveloppe de cercles. Ici $a=1.2$ et $b=2$

Limaçon de Pascal comme enveloppe de cercles - Animation. Ici $a\in [0.5,5]$ et $b=2$

Ovale de Descartes

Pour $a\neq b$, un limaçon de Pascal d'équation $\rho =a+b\cos \theta$ est un ovale de Descartes complet de foyers O et $F\left({\frac {b^{2}-a^{2}}{2b}},0\right)$ - foyer double - d'équation $\left|aOM\pm bF_{1}M\right|=bOF_{1}$

Pistes de démonstrations

Teixeira suggère de calculer la distance $\rho '=F_{1}M$ à l'aide de l'expression

$\rho '={\sqrt {\left(x-{\frac {b^{2}-a^{2}}{2b}}\right)^{2}+y^{2}}}$ en utilisant l'équation polaire du limaçon $\rho =a+b\cos \theta .$

On peut , grâce aux égalités $x=\rho \cos \theta$ et $x^{2}+y^{2}=\rho ^{2}$, puis $\cos \theta ={\frac {\rho -a}{b}}$, démontrer que

$\rho '={\frac {a}{b}}\rho +{\frac {b^{2}-a^{2}}{2b}}$ (quantité toujours positive)

Par conséquent

$a\rho -b\rho '=-b{\frac {b^{2}-a^{2}}{2b}}$

Il ne reste plus qu'à exploiter le fait que $OM=|\rho |$ et $OF_{1}=\left|{\frac {b^{2}-a^{2}}{2b}}\right|$ pour prouver que les points du limaçon sont sur l'ovale complet de foyers O et $F\left({\frac {b^{2}-a^{2}}{2b}},0\right)$ d'équation $\left|aOM\pm bF_{1}M\right|=bOF_{1}.$

Ou on peut, plus simplement, utiliser l'équation polaire de l'ovale de Descartes d'équation $|aOM\pm bF_{1}M|=|bOF_{1}|$ dans un repère de centre O pour obtenir

$(b^{2}-a^{2})\rho ^{2}-2{\frac {b^{2}-a^{2}}{2b}}(b^{2}\cos \theta +ab)\rho =0$

qui conduit, après simplification par $b^{2}-a^{2}$ aux solutions $\rho =0$ ou $\rho =b\cos \theta +a$

 

Notes et références

Bibliographie

• Francisco Gomes Teixeira, Traité des Courbes Spéciales Remarquables Planes et Gauches, t. 2, Coimbra, Imprensa da Universidade, 1909

  traduit de l’original en espagnol de 1899, revu et très augmenté. Réédition: dans les Obras sobre Matemática, volume V, 1908–1915; Chelsea Publishing Co, New York, 1971; Éditions Jacques Gabay, Paris, 1995 [lire en ligne].

• David Wells, Le dictionnaire Penguin des curiosités géométriques, Éditions Eyrolles, 2000
• Jean Aymes, Ces problèmes qui font les mathématiques : la trisection de l'angle, APMEP, 1988

Voir aussi

• Limaçon de Pascal sur MathCurve.
• (en) John J. O'Connor et Edmund F. Robertson, « Limacon of Pascal », sur MacTutor, université de St Andrews.