Trochoïde
Cet article est une ébauche concernant la géométrie.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
Une trochoïde est une courbe obtenue en traçant le mouvement décrit par un point lié à un disque roulant sans glisser sur une droite.
On doit ce terme au mathématicien Roberval (1602-1675) qui l'a adapté du grec ancien τροχοειδής, trokhoeidês (« circulaire, rond »)
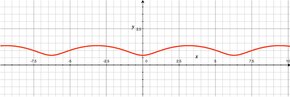
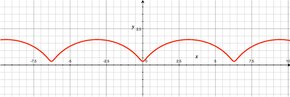
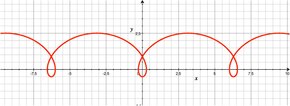
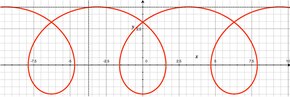
Soit un disque de rayon a roulant sans glisser sur une droite L. Le centre C se déplace parallèlement à L, et tous les autres points P du plan attaché au cercle décrivent une courbe appelée trochoïde. Si on nomme b la distance entre P et C, suivant que P se trouve dans le disque (b < a), ou sur sa circonférence (b = a), ou à l'extérieur (b > a), la trochoïde est dite raccourcie, commune ou encore allongée. Les équations paramétriques de la trochoïde, avec L sur l'axe des x, sont :
avec θ est la variable d'angle décrivant la rotation du cercle.
Une trochoïde raccourcie peut être décrite par le mouvement de la pédale d'une bicyclette (par rapport à la chaussée).
Une trochoïde allongée peut être décrite par les aubes d'un bateau à aubes à vitesse constante (par rapport à la rive).
On appelle cycloïde une trochoïde commune qui présente des points de rebroussement (ou cusps) là où P touche L.
Exemples
modifierLe physicien Franz Josef von Gerstner a montré que sous certaines conditions la houle des vagues décrit un mouvement trochoïdal. Voir l'article houle trochoïdale.
Dans la littérature
modifier- Espèce de trochoïde ! - 50 idées mathématiques expliquées au profane est le titre d'un ouvrage de Luc de Brabandere, écrit en collaboration avec Christophe Ribesse, aux éditions Dunod, en 2006, qui utilise dans son titre ce terme mathématique sous forme humoristique, laissant sous-entendre qu'il s'agit d'une insulte. L'ouvrage cherche à vulgariser un ensemble de notions mathématiques appliquées à la vie courante.
Voir aussi
modifier- Une hypotrochoïde est décrite par un disque roulant à l'intérieur d'un autre cercle fixé.
- Une épitrochoïde est décrite par un disque roulant à l'extérieur d'un autre cercle.
- Roulette (courbe)
Lien externe
modifier- Trochoïde sur MathCurve
