Théorème des valeurs intermédiaires
En mathématiques, le théorème des valeurs intermédiaires (abrégé en TVI), parfois appelé théorème de Bolzano[1], est un résultat important d'analyse sur les fonctions continues sur un intervalle. Il indique que si une fonction est continue sur un intervalle , alors elle prend toutes les valeurs intermédiaires entre et .
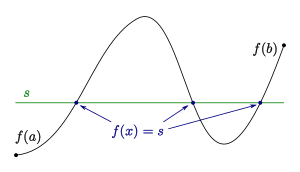
Ce théorème assure, dans certains cas, l'existence de solutions d'équations. Il constitue la base de techniques de résolution approchées comme la méthode de dichotomie. De plus, il est utilisé pour prouver d'autres théorèmes de continuité, tels que le théorème de la bijection.
Longtemps considéré comme évident, les premières tentatives de démonstration reposent essentiellement sur l'intuition géométrique. Bolzano est le premier à essayer de le démontrer sans utiliser l'intuition géométrique, mais il faudra attendre la fin du XIXe siècle et la construction des nombres réels pour avoir une démonstration entièrement rigoureuse.
Approche intuitive
modifierLa 10e étape du Tour de France 2008 était une course cycliste de 156 km de long partant de Pau (altitude : 200 m) et arrivant à Hautacam (1 520 m).
Le profil de l'étape est une fonction définie sur l'intervalle et à valeurs réelles. À tout nombre de , elle associe l'altitude du point situé à kilomètres du départ. Puisque les altitudes s'échelonnent de 200 à 1 520 m, il paraît évident que les coureurs ayant terminé l'étape ont dû passer au moins une fois par toutes les altitudes intermédiaires, c'est-à-dire les altitudes entre 200 et 1 520 m. Par exemple, le coureur passera au moins une fois par l'altitude 1 000 m. Cependant, cette constatation s'appuie sur deux hypothèses :
- le parcours est un intervalle, ce qui suppose que l'espace est un « continuum » – les mathématiciens parlent d'espace connexe – c'est-à-dire qu'il n'y a pas de « trou » entre 0 et 156.
- la fonction altitude est continue, ce qui signifie qu'une variation infinitésimale du kilométrage entraîne une variation infinitésimale de l'altitude. En d'autres termes, un coureur ne peut pas se téléporter instantanément d'une altitude à une autre.
Remarquons que le raisonnement n'est plus valable si le profil n'est plus défini sur un intervalle, par exemple si l'on ne s'intéresse qu'aux points de contrôle marqués sur le graphique ci-contre : il se peut qu'aucun de ces points, si nombreux soient-ils, ne se trouve à 1 000 m d'altitude.
Le théorème des valeurs intermédiaires formalise ce raisonnement empirique.
Le théorème des valeurs intermédiaires
modifierDéfinitions préliminaires
modifierComme vu dans l’approche intuitive, le théorème repose sur deux notions : la connexité et la continuité.
Dans , l’ensemble des nombres réels, les ensembles connexes correspondent aux intervalles. Un intervalle est l’ensemble des points contenus entre deux bornes. Par exemple l’intervalle est l’ensemble des tel que . En fonction de si les bornes sont incluses dans l’intervalle, on distingue les intervalles fermés , ouvert et semi-ouvert ou .
Une fonction est continue si à des variations infinitésimales de la variable correspondent des variations infinitésimales de la valeur . Autrement dit il n’y a pas de « sauts » dans le graphe de la fonction.
Énoncé
modifierThéorème des valeurs intermédiaires — Pour toute application continue et tout réel compris entre et , il existe au moins un réel compris entre et tel que .
Ce théorème se généralise sur un intervalle ouvert . Si admet une limite en et alors pour tout réel strictement entre ces limites, il existe au moins un réel tel que [2].
Plus généralement, les connexes de étant exactement les intervalles, est un intervalle[note 1] et donc :
Pour toute fonction définie et continue sur un intervalle de et à valeurs réelles, l'image est un intervalle de .
Attention : Le théorème n'affirme pas que l'image de l'intervalle par est l'intervalle . C'est faux, comme le montre le contre-exemple de la fonction avec et ; dans ce cas, mais .
Un cas particulier est le théorème de Bolzano.
Théorème de Bolzano — Si , il existe au moins un réel tel que .
En effet « » signifie que est compris entre et .
Réciproque
modifierIl n’y a pas de réciproque au théorème contrairement à ce qu’on a longtemps pensé (voir la section Histoire)[3]. Un contre-exemple est donné par la fonction définie par :
Cette fonction n'est pas continue en mais elle satisfait bien la propriété de la valeur intermédiaire pour chaque couple de réels[note 2]. Il existe même des fonctions discontinues en tout point et vérifiant quand même la propriété de la valeur intermédiaire, comme la fonction de Conway en base 13[4].
Cependant il y a équivalence entre :
- est continue sur
- Pour tout sous-intervalle inclus dans et tout y élément de , l'ensemble est une partie non vide et fermée de [5].
En particulier si elle ne prend chaque valeur qu'un nombre fini de fois, alors il y a équivalence de la propriété de la valeur intermédiaire avec la continuité[6].
Démonstrations
modifierLe théorème des valeurs intermédiaires fait partie des théorèmes dits d'existence. Cependant, il n'existe pas de démonstration générale constructive de cette existence[7].
Nous donnons ci-dessous deux démonstrations[note 3]. La première est courte mais s'appuie sur une théorie plus élaborée : la topologie. La seconde est basée sur la méthode de dichotomie et peut, dans une certaine mesure, être mise en œuvre numériquement.
Le théorème repose sur la complétude de . La démonstration originale de Bolzano et celle topologique utilisent la propriété de la borne supérieure de [8], et celle par dichotomie utilise le théorème des fermés emboîtés[note 4].
Dans , l'ensemble des nombres rationnels, le théorème est faux. Un contre-exemple, la fonction de dans est continue sur et vérifie et . Cependant, il n'y a pas de nombre rationnel tel que .
Démonstration topologique
modifierLa topologie fournit une démonstration en quelques lignes ces deux propriétés :
Les connexes de ℝ sont les intervalles.
L'image d'un connexe par une fonction continue est un connexe.
L'ensemble de départ est donc un connexe et son image par est donc un intervalle, ce qui démontre le théorème.
Mais derrière cette apparente simplicité se cachent des résultats qu'il faut avoir démontrés au préalable, comme le fait que tout intervalle de ℝ est connexe, démonstration du même ordre de difficulté que celle du théorème des valeurs intermédiaires.
Démonstration par dichotomie
modifierLe principe[note 5] consiste à couper le segment de départ en deux et à conserver l'intervalle où l'on sait que se trouve une solution. On recommence ensuite en coupant en deux le segment conservé, etc. On obtient ainsi une suite de segment emboîtés, et le théorème des fermés emboîtés nous assure de trouver une solution[9].
Cette méthode nous donne aussi un encadrement de la valeur cherchée, voir la section « Méthode de dichotomie ».
Applications
modifierLe théorème des valeurs intermédiaires est souvent utilisé pour montrer l'existence de solutions d’une équation, notamment l’existence de points fixes d'une fonction. Il permet aussi de démontrer d’autres théorèmes d'analyse, comme le théorème de la bijection ou celui affirmant que l'image d’un segment est un segment[note 6].
Méthode de dichotomie
modifierLa démonstration par dichotomie se traduit facilement sous forme algorithmique. À chaque itération, on divise l’intervalle en 2, puis on s’arrête quand sa longueur est inférieure à la précision demandée[10],[note 7].
Par ailleurs, la méthode de dichotomie ne permet de trouver qu'une seule valeur. Le fait d'éliminer tout un intervalle à chaque étape risque d'éliminer d'autres solutions. De plus, sa convergence n'est que linéaire[réf. nécessaire] : la précision n'augmente que d'un facteur 2 à chaque itération. D'autres méthodes comme la méthode de Newton ont une meilleurs efficacité.
L'avantage de la méthode est sa simplicité et qu'elle nécessite peu d'hypothèse : il suffit que soit continue et que et soient de signes opposés.
Théorème de la bijection
modifierUn corollaire important est le théorème de la bijection : en supposons la fonction strictement monotone en plus de continue, induit une bijection de dans . Cette bijection est même un homéomorphisme, c'est-à-dire que la bijection réciproque est également continue[11].
Ce théorème nous assure que des fonctions comme ou sont bien définies.
Existence de point fixe
modifierSi sont continue sur un intervalle de où si et sont de signes contraires, alors il existe au moins un tel que . En particulier en considérant , on peut montrer que a au moins un point fixe.
Racine des polynôme de degré impair
modifierSi est un polynôme de degré impair à coefficients réels, alors les limites de en et sont infinies et opposées (car est de degré impair) l’une de l’autre. Donc est une valeur intermédiaire et comme les fonctions polynomiales sont continues, il existe tel que par le théorème des valeurs intermédiaires. Ainsi tout polynôme réel de degré impair a au moins une racine réelle[12].
Histoire
modifierBryson d'Héraclée (en) proposa dès le Ve siècle av. J.-C., un théorème proche de celui des valeurs intermédiaires pour essayer de résoudre la quadrature du cercle[13].
Au XVIIe siècle plusieurs mathématiciens essayent de justifier le théorème. Cependant la notion de fonction venait à peine de naître et celle de continuité n'était encore qu'intuitive[14].
En 1817, Bolzano publie un article où il essaye de démontrer le théorème sans utiliser des « évidences géométriques »[15]. Pour lui :
« II n'y a absolument rien à objecter ni contre la justesse ni contre l'évidence de ce théorème géométrique. Mais il est tout aussi manifeste qu'il y a là une faute intolérable contre la bonne méthode, faute qui consiste à vouloir déduire les vérités mathématiques pures (ou générales) - c'est-à-dire de l'arithmétique, de l'algèbre ou de l'analyse - des considérations qui appartiennent à une partie appliquée (ou spéciale) seule, à savoir la géométrie. »[8]
— Bernard Bolzano
Sa démonstration le poussera à définir la notion de fonction continue et démontrer que a la propriété de la borne supérieure. Cependant sa définition reste floue et correspond plus à celle de continuité uniforme. De plus, une démonstration rigoureuse de la propriété de la borne supérieur dans n'est possible qu'en définissant rigoureusement l'ensemble des nombres réels, qui ne sera faites qu’une cinquantaine d’année plus tard[15].
Dans son Cours d'Analyse de l'École royale polytechnique publié en 1821, Cauchy donne un énoncé du théorème des valeurs intermédiaires comme le théorème IV du chapitre II, puis il en donne une démonstration[16]. Mais contrairement à Bolzano, Cauchy s'appuie sur des propriétés géométriques considérées comme évidentes qu'il ne prouve pas[17].
On a longtemps pensé que la réciproque était vraie, et que la propriété des valeurs intermédiaires caractérisait les fonctions continues[3]. Ce n’est qu’en 1875 que Darboux en donna un contre-exemple dans son article Mémoire sur les fonctions discontinues[18],[19].
Généralisations
modifierThéorème de Darboux
modifierLe théorème de Darboux généralise celui des valeurs intermédiaires aux fonctions dérivées[note 8]. Ainsi si est dérivable sur un intervalle , est un intervalle[20].
Des fonctions comme la dérivée de (c'est-à-dire , complétée par ), vérifient donc la propriété des valeurs intermédiaires sans être continues en .
Théorème de Poincaré-Miranda
modifierLe théorème suivant généralise le théorème des valeurs intermédiaires, plus précisément la formulation de Bolzano, dans un cube de dimension .
Soit une application continue telle que est strictement positive quand et est strictement négative quand . Alors il existe un point où s'annule[21].
Henri Poincaré l'a annoncé en 1883 puis démontré en 1886[22], mais ce n'est qu'en 1940 que Carlo Miranda (it) a remarqué[23] qu'il équivaut au théorème du point fixe de Brouwer.
En prenant dans ce théorème, on obtient bien le théorème de Bolzano.
Sur un espace topologique quelconque
modifierSoit un espace topologique connexe et une application continue. Le « théorème des valeurs intermédiaires généralisé[24] » dit que l'image est un intervalle.
On retrouve l'énoncé sur à partir de l'énoncé général à condition d'avoir démontré au préalable que tout intervalle réel est connexe (voir supra).
Notes et références
modifierNotes
modifier- En effet, l'image d'une partie connexe par une fonction continue est connexe. Voir par exemple le .
- En prenant , qui n'a pas de limite. Donc n'est pas continue, mais possède quand même la propriété des valeurs intermédiaires par le théorème de Darboux (voir section Généralisations).
- Il existe d'autres démonstrations, voir par exemple (en) Peter D. Lax et Maria Shea Terrell, Calculus With Applications, Springer, , 2e éd. (1re éd. 1976) (lire en ligne), p. 66-67 qui se rapproche plus de la démonstration originelle de Bolzano.
- Pour l'équivalence entre ces deux propriétés, voir Construction des nombres réels#Équivalence des deux constructions.
- Voir la .
- Le théorème des valeurs intermédiaires dit que l’image d’un segment est un intervalle. Avec le théorème des valeurs extrêmes, on montre que cet intervalle est un segment.
- Il n’est en général pas possible de demander , en raison des erreurs d’arrondi.
- Le théorème fondamental de l'analyse assurant l'existence d'une primitive pour les fonctions continues, elles sont donc un sous-ensemble des fonctions dérivées.
Références
modifier- Laurent Moonens (aspirant du FRS), « Bolzano et le théorème des valeurs intermédiaires » [PDF], sur AlmaSoror, (consulté le )
- .
- Ramis et Warusfel 2022, Remarque, p. 642.
- (en) Greg Oman, « The converse of the intermediate value theorem: from Conway to Cantor to cosets and beyond », Missouri Journal of Mathematical Sciences, vol. 26, no 2, , p. 134-150 (lire en ligne [PDF]).
- I. Gaber, A. Lev, R, Zigdon, « Insights and Observations on Teaching the Intermediate Value Theorem », Amer. Math. Monthly, vol. 126, no 9, , p. 845-849 (DOI 10.1080/00029890.2019.1647061)
- Spivak et 1967 p.109.
- Lire par exemple : Thierry Coquant, « Herbrand et le programme de Hilbert », Gazette de la SMF, no 118, , p. 17-18 (lire en ligne). Dans cet article est abordé la différence entre une existence formelle et une existence effective d'un objet en mathématique. Le théorème des valeurs intermédiaires est utilisé pour illustrer cette différence.
- Bolzano 1964.
- Daniel Perrin, « Deux démonstrations par dichotomie » [PDF], sur Université Paris-Sud (consulté le )
- Ramis et Warusfel 2022, Remarque, p. 635.
- Ramis et Warusfel 2022, Théorème 29, p. 637.
- Ramis et Warusfel 2022, Exercice 6, p. 636.
- (en) Henk J. M. Bos, Redefining Geometrical Exactness, New York, Springer, coll. « Sources and Studies in the History of Mathematics and Physical Sciences », , 472 p. (ISBN 978-1-4612-6521-4 et 978-1-4613-0087-8, DOI 10.1007/978-1-4613-0087-8 ), p. 26
- Hauchecorne et Dhombres 2023, p. 132.
- Dugac, Bru et Laurent 2003.
- Cauchy 1821.
- Hauchecorne et Dhombres 2023, p. 133-135.
- Darboux 1875.
- Hauchecorne et Dhombres 2023, p. 135-136.
- Spivak 1967, p. 253 (ex. 12)
- (en) Władysław Kulpa, « Poincaré and domain invariance theorem », Acta Univ. Carolin. Math. Phys., vol. 39, no 1, , p. 127-136 (lire en ligne [PDF])
- H. Poincaré, « Sur les courbes définies par une équation différentielle, IV », Journal de mathématiques pures et appliquées, vol. 85, , p. 151-217 (lire en ligne [PDF]).
- (it) Carlo Miranda, « Un'osservazione su una teorema di Brouwer », Bollettino dell'Unione Matematica Italiana, vol. 3, , p. 527.
- (en) Charles C. Pugh, Real Mathematical Analysis, Springer, (lire en ligne), p. 83
Voir aussi
modifierArticle connexe
modifierBibliographie
modifier: document utilisé comme source pour la rédaction de cet article.
Sources primaires
modifier- Bernard Bolzano (trad. J. Sebestik), « Démonstration purement analytique du théorème : entre deux valeurs quelconques qui donnent deux résultats de signes opposés se trouve au moins une racine réelle de l'équation. » [« Rein analytischer Beweis des Lehrsatzes, dass zwischen je zwei Werthen, die ein entgegengesetztes Resultat gewähren, wenigstens eine reelle Wurzel der Gleichung liege »], Revue d'histoire des sciences, vol. 17, no 2, , p. 136–164 (DOI 10.3406/rhs.1964.2325, lire en ligne , consulté le ) Traduction d'un article de Bolzano publié en 1817 à Prague. Dans ce texte, Bolzano réfute les démonstrations antérieures qui s'appuient sur des principes d'évidence ou des considérations géométriques. Il énonce le théorème p. 9, puis le démontre en utilisant la propriété de la borne supérieure p. 21-22.
- (en) S. B. Russ, « A translation of Bolzano's paper on the intermediate value theorem », Historia Mathematica, vol. 7, no 2, , p. 156-185 (DOI 10.1016/0315-0860(80)90036-1 )
- Augustin Louis Cauchy, Cours d'Analyse de l'École royale polytechnique, (lire en ligne) Dans cette démonstration, Cauchy se contente de l'évidence géométrique p. 43-44. Il ajoute cependant en note p. 460 un procédé numérique de résolution d'équation, assimilable à la démonstration par dichotomie du théorème des valeurs intermédiaires.
- (it) Giuseppe Peano, Calcolo differenziale e principii di calcolo integrale, (lire en ligne ) Après avoir défini les réels comme coupures de Dedekind, Peano donne une démonstration par dichotomie du théorème des valeurs intermédiaires.
- Gaston Darboux, « Mémoire sur les fonctions discontinues », Annales scientifiques de l'École normale supérieure, vol. 4, , p. 109 (ISSN 0012-9593 et 1873-2151, DOI 10.24033/asens.122, lire en ligne [PDF], consulté le ) Dans cet article Darboux énonce un contre-exemple à la réciproque du théorème des valeurs intermédiaires. Il montre que les fonctions dérivées (dont les fonctions continues font partie) vérifient aussi la propriété des valeurs intermédiaires. Ce résultat est maintenant connu comme le théorème de Darboux.
Sources secondaires
modifier- Bertrand Hauchecorne et Jean Dhombres, Biographie des grands théorèmes, Ellipses, , 243 p. (ISBN 978-2-340-08474-2), chap. 16 (« Théorèmes de la valeur intermédiaire, de Bolzano-Weierstrass et de Darboux »).
- Pierre Dugac, Bernard Bru et Roger Laurent, Histoire de l'analyse: autour de la notion de limite et de ses voisinages, Vuibert, , 419 p. (ISBN 978-2-7117-5311-6).
- (en) Michael Spivak, Calculus, Addison Wesley World Student Series, , 588 p. (ISBN 978-0-8053-9023-0, lire en ligne )
- Jean-Pierre Ramis (dir.), André Warusfel (dir.), Xavier Buff, Josselin Garnier, Emmanuel Halberstadt, François Moulin, Monique Ramis et Jacques Sauloy (préf. Alain Connes), Mathématiques Tout-en-un pour la Licence 1, Paris, Dunod, coll. « Sciences Sup », , 4e éd. (1re éd. 2006), 1040 p. (ISBN 978-2-10-084670-2, lire en ligne ), chap. 1.4 (« Théorème des valeurs intermédiaires et image continue d’un segment »)
Liens externes
modifier
- Notices dans des dictionnaires ou encyclopédies généralistes :
- « Théorème des valeurs intermédiaires - Dichotomie », sur Bibm@th (consulté le ).

![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


![{\displaystyle [a;b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68e776d74130a8890a814c1f4e74372a9110d2f9)
