Test de Student

En statistique, un test de Student, ou test t, désigne n'importe quel test statistique paramétrique où la statistique de test calculée suit une loi de Student lorsque l’hypothèse nulle est vraie.

Test de Student

Régions de rejet au niveau 10% d'un test de Student à 7 degrés de liberté.

Type	Test statistique, test paramétrique (d)
Inventeur	William Gosset (« Student »)

Histoire

Façade de la brasserie historique Guinness de St. James.

William Sealy Gosset, qui inventa le test t, sous le pseudonyme Student.

Le test de Student et la loi de probabilités qui lui correspond ont été publiés en 1908 dans la revue Biometrika par William Gosset. Gosset, un employé de la brasserie Guinness à Dublin, y avait développé le test t à des fins de contrôle de la qualité de la production de bière stout. La brasserie avait pour règle que ses chimistes ne publient pas leurs découvertes. Gosset argua que son article ne serait d'aucune utilité pour les concurrents et obtint l'autorisation de publier mais sous un pseudonyme, Student, pour éviter les difficultés avec les autres membres de son équipe.

Le test t est devenu célèbre grâce aux travaux de Ronald Fisher qui montra que ce test ne couvre pas le cas des échantillons de grande taille. Il apporta donc des modifications au test de Student afin de le généraliser.

Exemples d'utilisation

Le test t a plusieurs utilisations dont voici les plus fréquentes :

• Comparaison de moyenne d'une loi normale à une valeur si la variance est inconnue.
• Comparaison de deux moyennes issues de deux lois normales si leurs variances sont égales et inconnues. Dans le cas où leurs variances sont différentes et inconnues, on utilise une adaptation appelée le test t de Welch.
• Test sur les coefficients dans le cadre d'une régression linéaire.
• Test sur des échantillons appariés^[pas clair]

Test de Student sur un échantillon de loi normale

On considère une population de loi normale de moyenne μ et d'écart type σ. L'écart type σ n'est pas connu. On souhaite tester si la moyenne μ est égale à une valeur déterminée μ₀. L'hypothèse nulle est H₀ : μ = μ₀, autrement dit on suppose a priori que la moyenne vaut μ₀. On se place maintenant sous l'hypothèse nulle.

Cadre

On considère un échantillon de taille n de cette population $(X_{1},\dots ,X_{n})$, autrement dit, selon l'hypothèse nulle, chaque $X_{i}$ est une variable aléatoire qui suit une loi normale de moyenne μ₀ et d'écart type σ. De plus, les $X_{i}$ sont indépendantes. On estime alors la moyenne par la moyenne empirique :

${\overline {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}$ .

Comme l’hypothèse nulle est supposée vraie, la moyenne ${\overline {X}}$ suit également une loi normale d'espérance μ₀, mais d'écart type σ/√n. Comme la variance σ² est inconnue, on l'estime par son estimateur sans biais (on note la division par $n-1$ au lieu de $n$ afin d'avoir un estimateur sans biais) :

$S_{n}^{\ast ^{2}}={\frac {1}{n-1}}\sum \limits _{i=1}^{n}(X_{i}-{\overline {X}}_{n})^{2}$.

Définition de la statistique

D'après le théorème de Cochran, sous l'hypothèse nulle, ${\frac {n-1}{\sigma ^{2}}}S_{n}^{\ast ^{2}}$suit une loi du chi deux à n – 1 degrés de liberté.

On pose la statistique de test suivante :

$Z={\sqrt {n}}{\frac {{\overline {X}}-\mu _{0}}{S_{n}^{\ast }}}$

Par définition, la statistique $Z$ suit une loi de Student à n – 1 degrés de liberté. La réalisation de la statistique de test :

$z={\sqrt {n}}{\frac {{\overline {x}}_{n}-\mu _{0}}{s_{n}^{\ast }}},$ où $s_{n}^{\ast }={\sqrt {{\frac {1}{n-1}}\sum \limits _{i=1}^{n}(x_{i}-{\overline {x}}_{n})^{2}}}$.

Mise en place du test

Fonction de densité de la loi de Student à 7 degrés de liberté. La zone rouge est la région de rejet.

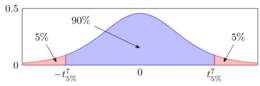
On rappelle que l'on veut tester H₀ : μ = μ₀. On choisit un risque α, généralement 0,05 ou 0,01^{[réf. nécessaire]}. Le risque α s'appelle risque de première espèce, c'est la probabilité de rejeter $H_{0}$ dans le cas où $H_{0}$ est vraie. La figure ci-contre correspond à un risque $\alpha$ de 0,1 et $n=8$, et donc une loi de Student avec $n-1=7$ degrés de liberté. La figure montre le quantile d'ordre $\alpha \over 2$ (à gauche) et celui d'ordre $1-{\frac {\alpha }{2}}$ (à droite). Comme la loi de Student est symétrique, ces quantiles sont égaux au signe près.

• Si la valeur de $z$ (sur l'axe des abscisses) est dans la zone bleue (entre les deux quantiles), alors on conserve l'hypothèse nulle.
• Si elle est dans la zone rouge, on rejette l'hypothèse nulle.

Dit autrement, si |z| est supérieur au quantile d'ordre 1 – α/2 de la loi de Student à n – 1 degrés de liberté alors on rejette l'hypothèse nulle.

Variantes

Fonction de densité de la loi de Student à 7 degrés de liberté (toujours et encore) mais cette fois la région de rejet pour tester $\mu \leq \mu _{0}$.

Examinons la variante où cherche à tester l'hypothèse nulle H₀ : μ ≤ μ₀. Dans ce cas, une valeur de z négative n'est pas discriminante et si z est dans la région bleue de la figure ci-contre alors on conserve l'hypothèse nulle. Par contre, si z est supérieur au quantile d'ordre 1 – α de la loi de Student à n – 1 degrés de liberté alors on rejette l'hypothèse nulle (région rouge à droite pour un risque de $\alpha$ = 10%).

Fonction de densité de la loi de Student à 7 degrés de libertés (encore et toujours) mais cette fois la région de rejet pour tester pour $\mu \geq \mu _{0}$.

Tester H₀ : μ ≥ μ₀ se fait de manière symétrique. Cette fois ci, des valeurs positives de z ne sont pas discrimantes. Si z est inférieur au quantile d'ordre α de la loi de Student à n – 1 degrés de liberté (région rouge à gauche pour un risque de $\alpha$ = 10% dans la figure) alors on rejette l'hypothèse nulle.

Implémentation

Langage/Logiciel	Fonction	Notes
R	t.test	[1]
SAS	PROC TTEST	[2]
Python	scipy.stats.ttest_ind	[3]
Matlab	ttest	[4]
Mathematica	TTEST	[5]
Stata	ttest	[6]
Julia	OneSampleTTest EqualVarianceTTest	[7]
Maple	OneSampleTTest, TwoSampleTTest, TwoSamplePairedTTest

Voir aussi

• Loi de Student, la loi de probabilité de la statistique dans le test t
• Test t de Welch, une adaptation pour comparer deux moyennes de deux lois normales dont les variances sont inconnues et inégales
• Test de Wald