Portail:Mathématiques/Galerie
-
Illustration de l'algorithme de tri rapide.
-
Alvéoles d'abeilles dont une coupe transversale illustre le pavage hexagonal du plan.
-
Entrelacs des anneaux borroméens.
-
Arbre fractal.
-
Le théorème de la boule chevelue stipule qu'un champ de vecteurs tangents continu sur une sphère s'annule toujours en au moins un point.
-
Les cercles de Ford tangents extérieurement et dont les abscisses des centres se répartissent selon les suites de Farey.
-
Comparaison des graphies des chiffres arabes.
-
Chou romanesco présentant une structure fractale.
-
Cycle d'un canon à planeurs dans l'automate cellulaire du jeu de la vie inventé par le mathématicien britannique John Horton Conway.
-
Représentation en projection orthogonale de l'attracteur de Lorenz, symbole de l'effet papillon dans la théorie du chaos.
-
Corde lovée en spirale d'Archimède mais dont les rainures forment en sens inverse des spirales logarithmiques ou équiangles.
-
Animation montrant la recherche des nombres premiers inférieurs à 100 par utilisation du crible d'Ératosthène (cliquer sur l'image pour lancer l'animation).
-
Représentation d'un ensemble de Julia, un cas particulier de fractale obtenu à l'aide d'un système dynamique dans le plan complexe.
-
L'ensemble de Mandelbrot, exemple fondamental de fractale du plan et visualisé pour la première fois en 1980 par Benoit Mandelbrot.
-
Quatrième étape de construction de l'éponge de Menger, une fractale de l'espace.
-
Représentation du plan de Fano à sept éléments par un graphe : les droites de ce plan projectif sont représentés par les alignements et les cercles.
-
Illustration de l'identité remarquable du développement du carré algébrique par un découpage du carré géométrique.
-
Bassins d'attraction pour la méthode de Newton appliquée à une fonction du troisième degré, donnant un exemple de découpage du plan en lacs de Wada.
-
Le mathématicien Henri Poincaré (1854-1912), fondateur entre autres de la topologie algébrique et auteur d'une conjecture démontrée en 2003 par Grigori Perelman.
-
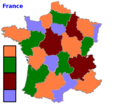
Le théorème des quatre couleurs affirme que toute carte dont les territoires sont d'un seul tenant avec des frontières simples à la surface de la sphère peut être coloriée avec quatre couleurs seulement de façon à ce que deux territoires ayant une frontière commune soient toujours de couleurs différentes.
-
Un quipu, système de codage d'entiers naturels à l'aide de nœuds sur des cordelettes, utilisé par l'administration inca.
-
Un Rubik's Cube, casse-tête dont l'espace des configurations peut être décrit à l'aide des permutations sur les sommets et les arêtes.
-
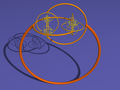
Sphère cornue d'Alexander, homéomorphe à une sphère mais dont le complémentaire n'est pas simplement connexe.
-
Spirale d'or de Martina Schettina pour la biennale d'art sur la lumière en 2010 en Autriche.
-
Jeu du taquin, dont l'ensemble des configurations admissibles est décrit par le groupe alterné de rang 15.
-
Projection 3D d'un hypercube quadridimensionnel exécutant une double rotation sur deux plans orthogonaux.
-
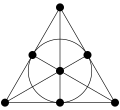
Configuration de points en triangle comme dans la tetraktys grecque, montrant que 10 est un nombre triangulaire.
-
Tours de Hanoï, dont la résolution peut être présentée à l'aide d'un algorithme récursif.
-
Tresse à trois brins, représentant une tresse mathématique obtenue par produit alterné des deux générateurs fondamentaux.
-
Premières lignes du triangle de Pascal dans lequel les termes impairs tracent les premières étapes d'un triangle de Sierpiński.
-
Application de la transformation du photomaton à la représentation de la Joconde.
-
La tablette d'argile YBC 7289 datant du IIe millénaire av. J.-C. et comportant une approximation de la racine carrée de deux dans le système sexagésimal de la numération babylonienne.