Spirale d'or
En géométrie, une spirale d'or est une spirale logarithmique avec un facteur de croissance de , appelé nombre d'or[1]. Une spirale d'or devient plus large par un facteur de φ pour chaque quart de tour qu'elle fait.
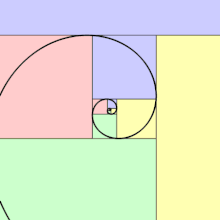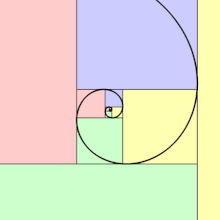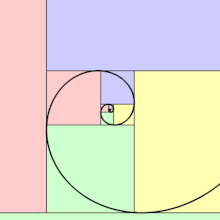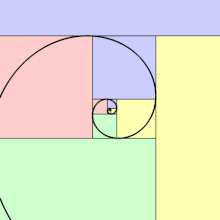
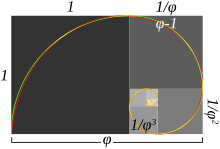
Formule
modifierLa spirale d'or est la courbe d'équation polaire suivante[2] :
ou encore :
avec e la base des logarithmes naturels, a étant une constante réelle strictement positive arbitraire et b donné par :
Voir aussi
modifierNotes et références
modifier(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Golden spiral » (voir la liste des auteurs).
- Chang, Yu-sung, "Golden Spiral « https://web.archive.org/web/20190728084311/http://demonstrations.wolfram.com/GoldenSpiral/ »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?), ", The Wolfram Demonstrations Project.
- Priya Hemenway, Divine Proportion: Φ Phi in Art, Nature, and Science, Sterling Publishing Co, , 127–129 p. (ISBN 1-4027-3522-7)
