En théorie des probabilités et en statistique , la loi de Rademacher est une loi de probabilité discrète ayant une probabilité 1/2 d'obtenir 1 et 1/2 d'obtenir -1. Le nom de cette loi vient du mathématicien Hans Rademacher .
loi de Rademacher
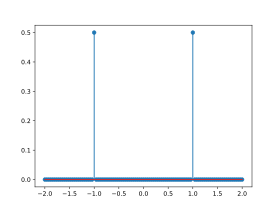
Fonction de masse
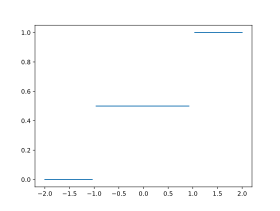
Fonction de répartition
Support
k
∈
{
−
1
,
1
}
{\displaystyle k\in \{-1,1\}\,}
Fonction de masse
f
(
k
)
=
{
1
/
2
,
k
=
−
1
1
/
2
,
k
=
1
{\displaystyle f(k)={\begin{cases}1/2,&k=-1\\1/2,&k=1\end{cases}}}
Fonction de répartition
F
(
k
)
=
{
0
,
k
<
−
1
1
/
2
,
−
1
≤
k
<
1
1
,
k
≥
1
{\displaystyle F(k)={\begin{cases}0,&k<-1\\1/2,&-1\leq k<1\\1,&k\geq 1\end{cases}}}
Espérance
0
{\displaystyle 0\,}
Médiane
0
{\displaystyle 0\,}
Mode
N/A
Variance
1
{\displaystyle 1\,}
Asymétrie
0
{\displaystyle 0\,}
Kurtosis normalisé
−
2
{\displaystyle -2\,}
Entropie
ln
(
2
)
{\displaystyle \ln(2)\,}
Fonction génératrice des moments
cosh
(
t
)
{\displaystyle \cosh(t)\,}
Fonction caractéristique
cos
(
t
)
{\displaystyle \cos(t)\,}
modifier
Cette loi correspond au gain lors d'un jeu de pile ou face dans lequel la mise est de 1 : un joueur a une probabilité de 1/2 de gagner, c'est-à-dire gagner 1, et 1/2 de perdre, c'est-à-dire gagner -1
La fonction de masse de la loi de Rademacher est donnée par :
f
(
k
)
=
{
1
/
2
si
k
=
−
1
,
1
/
2
si
k
=
+
1
,
0
sinon.
{\displaystyle f(k)=\left\{{\begin{matrix}1/2&{\mbox{si }}k=-1,\\1/2&{\mbox{si }}k=+1,\\0&{\mbox{sinon.}}\end{matrix}}\right.}
Elle peut également être écrite de manière équivalente :
f
=
1
2
1
1
{
−
1
,
1
}
.
{\displaystyle f={\frac {1}{2}}}1\!\!\!1_{\{-1,1\}.}
La fonction de répartition de la loi de Rademacher est donnée par :
F
(
k
)
=
{
0
,
si
k
<
−
1
1
/
2
,
si
−
1
≤
k
<
1
1
,
si
k
≥
1
{\displaystyle F(k)={\begin{cases}0,&{\mbox{si }}k<-1\\1/2,&{\mbox{si }}-1\leq k<1\\1,&{\mbox{si }}k\geq 1\end{cases}}}
Loi de Bernoulli : Si X suit la loi de Rademacher, alors
X
+
1
2
{\displaystyle {\frac {X+1}{2}}}
1
2
{\displaystyle {\frac {1}{2}}}