Graphe de Halin
En théorie des graphes, une branche des mathématiques, un graphe de Halin est un graphe planaire construit à partir d'un arbre en reliant toutes ses feuilles dans un cycle qui fait le tour de l'arbre de telle façon que l'arbre reste planaire. On exige de plus que l'arbre comporte au moins quatre sommets et ne comporte pas de sommets de degré 2[1].
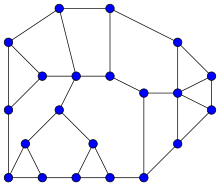
Les graphes de Halin graphs sont nommés d'après le mathématicien allemand Rudolf Halin qui les a étudiés en 1971[2], mais les graphes de Halin cubiques avaient déjà été étudiés plus d'un siècle auparavant par Thomas Kirkman[3].
Exemples
modifierLes graphes roue (les graphes des arêtes d'une pyramide) sont des graphes de Halin ; leur arbre est un graphe étoile.
Le graphe des arêtes d'un prisme triangulaire est également un graphe de Halin (figure).
Le graphe de Frucht, un des plus petits graphes cubiques sans automorphisme de graphe trivial, est aussi un graphe de Halin.
Propriétés
modifier- Tout graphe de Halin est un graphe planaire au nombre minimal d'arêtes qui est 3-connexe[1]. Le théorème de Steinitz (en) permet d'en déduire que c'est un graphe polyédrique.
- Tout graphe de Halin a un plongement planaire unique, au choix près de l’espace extérieur, c'est-à-dire un unique plongement dans une 2-sphère[1].
- Tout graphe de Halin est hamiltonien, et chaque arête du graphe appartient à un cycle hamiltonien. De plus, un graphe de Halin reste hamiltonien lorsque l'on supprime n'importe quel sommet[4].
- Tout graphe de Halin est presque pancyclique, dans le sens où il comporte des cycles de toutes les longueurs de à (le nombre de sommets) sauf éventuellement une unique longueur paire. De plus, un graphe de Halin reste presque pancyclique si une seule arête est contractée. Enfin, un graphe de Halin sans sommets intérieurs de degré 3 est pancyclique[5].
- Tout graphe de Halin a une largeur arborescente inférieure ou égale à 3[6]. Par conséquent, beaucoup de problèmes qui sont NP-complets dans le cas général, comme la recherche d'un stable de taille maximum, peuvent être résolus en durée linéaire dans le cas des graphes de Halin en s'appuyant sur de la programmation dynamique[7].
- Tout graphe de Halin contient un triangle. En effet, chaque arbre sans sommets de degré 2 contient au moins deux feuilles qui partagent le même parent. En particulier, un graphe de Halin ne peut par être un graphe sans triangle ni un graphe biparti.
- Le dual faible d'un graphe de Halin est biconnexe et planaire extérieur. Un graphe planaire est un graphe de Halin si et seulement si son dual faible est biconnexe et planaire extérieur[8].
Historique
modifierEn 1971, Halin a introduit les graphes de Halin comme une sorte de graphes au moins 3-connexes, en faisant remarquer que la suppression de n'importe quelle arête du graphe changeait le degré de connexité du graphe. Ces graphes ont gagné en importance lorsque l'on a découvert que de nombreux problèmes algorithmiques qui étaient difficiles à résoudre par calcul pour des graphes planaires arbitraires pouvaient être résolus efficacement avec eux[4],[8], une propriété qui a été expliquée plus tard comme une conséquence de leur faible largeur arborescente[6],[7].
Avant les travaux de Halin sur ces graphes, des problèmes d'énumération de graphes (en) concernant les graphes de Halin cubiques ont été étudiés en 1965 par Hans Rademacher[9]. Rademacher définit ces graphes (qu'il appelle based polyhedra, polyèdres à base) comme les graphes polyédriques cubiques dans lesquels une des faces comporte côtés, où est le nombre de faces du polyèdre. Il mentionne lui-même des travaux bien antérieurs publiés en 1856 par Thomas Kirkman sur la même classe de graphes[3]
Les graphes de Halin sont parfois également appelés roofless polyhedra (polyèdres à ciel ouvert)[4], mais, comme based polyhedra, ce nom peut aussi faire référence aux graphes de Halin cubiques[10].
Notes et références
modifier- (en) « Halin graph », dans Michiel Hazewinkel, Encyclopædia of Mathematics, Springer, (ISBN 978-1556080104, lire en ligne)
- (en) R. Halin, « Studies on minimally n-connected graphs », dans Combinatorial Mathematics and its Applications (Proc. Conf., Oxford, 1969), London, Academic Press, , p. 129-136, lien Math Reviews
- (en) Th. P. Kirkman, « On the enumeration of x-edra having triedral summits and an (x − 1)-gonal base », Philosophical Transactions of the Royal Society of London, , p. 399–411 (JSTOR 108592).
- (en) G. Cornuéjols, D. Naddef et W. R. Pulleyblank, « Halin graphs and the travelling salesman problem », Mathematical Programming, vol. 26, no 3, , p. 287–294 (DOI 10.1007/BF02591867).
- Mirosława Skowrońska, « The pancyclicity of Halin graphs and their exterior contractions », dans Cycles in Graphs, vol. 27, Elsevier Science Publishers B.V., , p. 179–194.
- (en) Hans L. Bodlaender, « Planar graphs with bounded treewidth », Technical Report RUU-CS-88-14, Département d'informatique, Université d'Utrecht, (lire en ligne).
- (en) Hans L. Bodlaender, « Dynamic programming on graphs with bounded treewidth », dans Proceedings of the 15th International Colloquium on Automata, Languages and Programming, vol. 317, Springer-Verlag, , p. 105–118.
- (en) Maciej M. Sysło et Andrzej Proskurowski, « On Halin graphs », dans Graph Theory: Proceedings of a Conference held in Lagów, Poland, February 10–13, 1981, vol. 1018, Springer-Verlag, (DOI 10.1007/BFb0071635), p. 248–256.
- (en) Hans Rademacher, « On the number of certain types of polyhedra », Illinois Journal of Mathematics, vol. 9, , p. 361–380 (MR 0179682, lire en ligne).
- (en) L. Lovász et M. D. Plummer, « On a family of planar bicritical graphs », dans Combinatorics (Proc. British Combinatorial Conf., Univ. Coll. Wales, Aberystwyth, 1973), Londres, Cambridge Univ. Press, , 103–107 p. (MR 0351915), chap. 13.
Source
modifier- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Halin graph » (voir la liste des auteurs).
Liens externes
modifier- (en) Halin graph, Information System on Graph Class Inclusions.
- (en) Eric W. Weisstein, « Halin Graph », sur MathWorld