Graphe de Clebsch
Le graphe de Clebsch est, en théorie des graphes, un graphe 5-régulier possédant 16 sommets et 40 arêtes. Il a été nommé ainsi à cause de son lien avec la surface quartique (en) découverte par Alfred Clebsch en 1868. On le connait aussi sous le nom de graphe de Greenwood–Gleason, à cause des travaux de Robert E. Greenwood et Andrew Gleason en 1955.
| Graphe de Clebsch | |
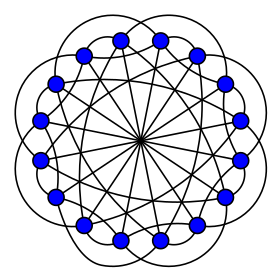 Représentation du graphe de Clebsch | |
| Nombre de sommets | 16 |
|---|---|
| Nombre d'arêtes | 40 |
| Distribution des degrés | 5-régulier |
| Rayon | 2 |
| Diamètre | 2 |
| Maille | 4 |
| Automorphismes | 1 920 |
| Nombre chromatique | 4 |
| Indice chromatique | 5 |
| Propriétés | Fortement régulier Hamiltonien Cayley |
| modifier |
|
Construction
modifierOn peut construire le graphe de Clebsch en reliant par huit nouvelles arêtes les sommets opposés d'un hypercube en quatre dimensions (c'est-à-dire les sommets à distance quatre l'un de l'autre).
Une autre construction est de fusionner les sommets opposés de l'hypercube en cinq dimensions (donc les sommets à une distance cinq l'un de l'autre).
La construction historique est la suivante :
- on représente les 16 droites contenues dans la quartique de Clebsch[1] par 16 sommets d'un graphe ;
- on relie deux de ces sommets si et seulement si les droites correspondantes ne sont ni parallèles ni sécantes.
On obtient également le graphe de Clebsch en représentant les éléments du corps fini GF(16) par des sommets, et en les reliant lorsque leur différence dans GF(16) est un nombre cubique[2].
Propriétés
modifierPropriétés générales
modifierLe graphe de Clebsch est un graphe fortement régulier de paramètres [3],[4].
Le diamètre du graphe de Clebsch, l'excentricité maximale de ses sommets, est 2, son rayon, l'excentricité minimale de ses sommets, est 2 et sa maille, la longueur de son plus court cycle, est 4, c'est donc un graphe sans triangle. Il s'agit d'un graphe 5-sommet-connexe et d'un graphe 5-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 5 sommets ou de 5 arêtes.
Le graphe de Clebsch est également un graphe non-planaire, un graphe non-eulérien et un hamiltonien.
Coloration
modifierLe nombre chromatique du graphe de Clebsch est 4. C'est-à-dire qu'il est possible de le colorer avec 4 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes mais ce nombre est minimal. Il n'existe pas de 3-coloration valide du graphe.
L'indice chromatique du graphe de Clebsch est 5. Il existe donc une 5-coloration des arêtes du graphe telle que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.
-
Le nombre achromatique du graphe de Clebsch est 8.
-
Le nombre chromatique du graphe de Clebsch est 4.
-
L'indice chromatique du graphe de Clebsch est 5.
Propriétés algébriques
modifierLe groupe d'automorphismes du graphe de Clebsch est d'ordre 1 920. Il est isomorphe au groupe de Coxeter D5. Ce groupe d'automorphismes agit transitivement sur l'ensemble des sommets du graphe de Clebsch, faisant de lui un graphe sommet-transitif[5].
Le polynôme caractéristique de la matrice d'adjacence du graphe de Clebsch est : . Il n'admet que des racines entières. Le graphe de Clebsch est donc un graphe intégral, un graphe dont le spectre est constitué d'entiers[5].
Graphe complémentaire
modifierLe graphe complémentaire du graphe de Clebsch est un graphe 10-régulier. Il est lui aussi fortement régulier[5]. Il s'agit du graphe demi-hypercube construit à partir de l'hypercube en 5 dimensions (penteract). Pour le construire, on relie les sommets qui sont à une distance 2 dans l'hypercube ; cela donne deux graphes isomorphes dont on ne garde que l'un des deux.
C'est ce graphe 10-régulier, à 16 sommets et à 80 arêtes que certains auteurs comme J. J. Seidel (en 1968) ou Andries Brouwer appellent « graphe de Clebsch »[6],[7]. Le graphe décrit par Clebsch un siècle plus tôt, dans son article de 1868, est néanmoins bien le graphe 5-régulier[1].
Divers
modifierSoit un sommet quelconque du graphe de Clebsch. Le sous-graphe induit aux 10 sommets qui ne sont pas des voisins de est le graphe de Petersen.
Notes et références
modifier- (de) Alfred Clebsch, « Ueber die Flächen vierter Ordnung, welche eine Doppelcurve zweiten Grades besitzen », Journal für die reine und angewandte Mathematik, vol. 69, , p. 142-184 (lire en ligne)
- (en) Frank De Clerck, « Constructions and Characterizations of (Semi)partial Geometries », dans Summer School on Finite Geometries, (lire en ligne), p. 6
- (en) C.D. Godsil, « Problems in algebraic combinatorics », Electron. J. Combin., vol. 2, , p. 3 (lire en ligne, consulté le )
- (en) Peter J. Cameron Strongly regular graphs sur DesignTheory.org, 2001
- (en) The Clebsch Graph sur la page personnelle de Bill Cherowitzo
- (en) Eric W. Weisstein, « Halved cube graph », sur MathWorld
- (en) Andries E. Brouwer, Clebsch graph
Voir aussi
modifierArticle connexe
modifierLien externe
modifier- (en) Eric W. Weisstein, « Clebsch Graph », sur MathWorld