Hypothèse de Riemann
En mathématiques, l'hypothèse de Riemann est une conjecture formulée en 1859 par le mathématicien allemand Bernhard Riemann, selon laquelle les zéros non triviaux de la fonction zêta de Riemann ont tous une partie réelle égale à 1/2. Sa démonstration améliorerait la connaissance de la répartition des nombres premiers et ouvrirait des nouveaux domaines aux mathématiques.
Cette conjecture constitue l'un des problèmes non résolus les plus importants des mathématiques du début du XXIe siècle : elle est l'un des vingt-trois fameux problèmes de Hilbert proposés en 1900, l'un des sept problèmes du prix du millénaire et l'un des dix-huit problèmes de Smale. Comme pour les six autres problèmes du millénaire, l'énoncé exact de la conjecture à démontrer est accompagné d'une description détaillée[1], fournissant de nombreuses informations sur l'historique du problème, son importance, et l'état des travaux à son sujet[2] ; beaucoup des remarques informelles de cette page en proviennent.
La fonction zêta de Riemann
modifierLa fonction zêta de Riemann est définie pour tous les nombres complexes s de partie réelle strictement supérieure à 1 par
Leonhard Euler l’introduit (sans lui donner de nom) uniquement pour des valeurs réelles de l’argument (mais aussi pour ), en liaison, entre autres, avec sa solution du problème de Bâle. Il montre[3] qu'elle est donnée par le produit eulérien où le produit infini porte sur tous les nombres premiers p, mais ne converge pas forcément : en effet, dans le Théorème 7 de son article, Euler donne une démonstration de cette formule pour le cas (tout en notant que ), et il l’établit en général dans son Théorème 8. C'est ce résultat qui explique l'intérêt de la fonction zêta dans l'étude de la répartition des nombres premiers (Euler déduit par exemple du cas , dans le Théorème 19 du même article[3] que la série des inverses des nombres premiers est divergente). Le résultat reste bien entendu valable lorsque l’argument est complexe.
L'hypothèse de Riemann porte sur les zéros de cette fonction en dehors du domaine de convergence qu'on vient de voir, ce qui peut sembler n'avoir aucun sens. L'explication tient dans la notion de prolongement analytique : on peut démontrer qu'il existe une fonction holomorphe unique définie pour tout complexe (différent de 1, où elle présente un pôle simple) et coïncidant avec zêta pour les valeurs où cette dernière est définie ; on note encore ζ(s) cette nouvelle fonction.
L'une des techniques[4] pour construire ce prolongement est la suivante.
- Il est d'abord facile de vérifier que, pour s de partie réelle > 1, on a :
or la série de droite (appelée fonction êta de Dirichlet) converge pour tout s de partie réelle strictement positive[5]. On prolonge ainsi ζ à tous les s ≠ 1 de partie réelle > 0 (même ceux de la forme 1 + 2ikπ/ln(2) avec k entier non nul, car on montre qu'en ces points, la fonction possède une limite finie).
- On montre ensuite, pour tout s de partie réelle strictement comprise entre 0 et 1, l'identité fonctionnelle[6] où Γ est la fonction Gamma d'Euler. Il devient alors possible d'utiliser cette formule pour définir zêta pour tout s de partie réelle négative (avec ζ(0) = –1/2 par passage à la limite).
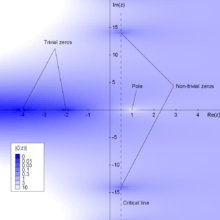
On en déduit que les entiers pairs strictement négatifs sont des zéros de zêta (appelés zéros triviaux) et que les zéros non triviaux sont symétriques par rapport à l'axe Re(s) = 1/2 et sont tous de partie réelle comprise, au sens large, entre 0 et 1 ; cette région du plan complexe s'appelle la bande critique.
De plus, il n'y a aucun zéro sur l'axe Re(s) = 1 (ce résultat est équivalent au théorème des nombres premiers[7], voir section historique ci-dessous). Du coup, l'hypothèse de Riemann peut se reformuler ainsi : si 0 < Re(s) < 1 et si s est un zéro de ζ (ou, ce qui revient au même, de η), alors sa partie réelle vaut 1/2.
Historique de la conjecture
modifier« […] es ist sehr wahrscheinlich, dass alle Wurzeln reell sind. Hiervon wäre allerdings ein strenger Beweis zu wünschen; ich habe indess die Aufsuchung desselben nach einigen flüchtigen vergeblichen Versuchen vorläufig bei Seite gelassen, da er für den nächsten Zweck meiner Untersuchung entbehrlich schien. »
« […] il est fort probable que toutes les racines soient réelles. Bien sûr, une démonstration rigoureuse en serait souhaitable ; pour le moment, après quelques vagues tentatives restées vaines, j'ai provisoirement mis de côté la recherche d'une preuve, car elle semble inutile pour l'objectif suivant de mes investigations. »
— énoncé par Riemann de l'hypothèse, dans l'article de 1859 ; Riemann y parle d'une fonction obtenue à partir de zêta, dont toutes les racines devraient être réelles plutôt que sur la ligne critique.
Riemann mentionna la conjecture, appelée plus tard « hypothèse de Riemann », dans son article paru en 1859, Sur le nombre de nombres premiers inférieurs à une taille donnée (Über die Anzahl der Primzahlen unter einer gegebenen Grösse en allemand)[8], dans lequel il donnait une formule explicite pour le nombre de nombres premiers π(x) inférieurs à un nombre donné x.
Cette formule affirme que les zéros de la fonction zêta contrôlent les oscillations des nombres premiers autour de leur position « attendue ». Riemann savait que les zéros non triviaux de zêta étaient distribués symétriquement autour de l'axe s = ½ + it, et aussi qu'ils devaient tous être dans la bande critique 0 ≤ Re(s) ≤ 1. Il vérifia que les premiers zéros avaient pour partie réelle exactement 1/2 (ce point sera discuté plus bas ; il s'agit bien d'une démonstration, et non d'un calcul numérique approché) et suggéra qu'ils pourraient bien être tous sur l'axe de symétrie (la ligne critique) Re(s)=1/2 ; c'est cette conjecture qu'on appelle l'hypothèse de Riemann.
En 1896, Hadamard et La Vallée-Poussin prouvèrent indépendamment qu'aucun zéro ne pouvait se trouver sur la ligne Re(s) = 1, et donc que tous les zéros non triviaux devaient se trouver dans l'intérieur de la bande critique 0 < Re(s) < 1. Ceci s'avéra être un résultat-clé dans la première démonstration complète du théorème des nombres premiers.
En 1900, Hilbert inclut l'hypothèse de Riemann dans sa célèbre liste de 23 problèmes non résolus : c'est le 8e problème. Il aurait dit à son propos : « Si je devais me réveiller après avoir dormi pendant mille ans, ma première question serait : l'hypothèse de Riemann a-t-elle été prouvée[9] ? ».
En 1914, Hardy prouva qu'il y a une infinité de zéros sur la droite critique Re(s) = 1/2. Cependant il reste possible qu'il y ait une infinité de zéros non triviaux ailleurs. Des travaux ultérieurs de Hardy et Littlewood en 1921, puis de Selberg en 1942 ont donné une estimation de la densité moyenne de zéros sur la droite critique.
Des travaux plus récents se sont focalisés sur le calcul explicite d'endroits où se trouvent beaucoup de zéros (dans l'espoir de trouver un contre-exemple) et de placer des bornes supérieures sur la proportion de zéros se trouvant ailleurs que sur la droite critique (dans l'espoir de la réduire à zéro).
L'hypothèse de Riemann est l'un des sept problèmes de Hilbert non encore résolus, et fut d'ailleurs le seul problème de Hilbert choisi pour figurer dans la liste des problèmes du prix du millénaire de l'institut de mathématiques Clay.
Tests numériques
modifierDès l'énoncé par Riemann de la conjecture, des calculs numériques des premiers zéros non triviaux de la fonction permirent de la confirmer (on trouvera dans la table ci-dessous un exposé des divers résultats obtenus). Dans les années 1980, Andrew Odlyzko s'était spécialisé dans ce type de calcul, et on affirme ainsi généralement que le milliard et demi de zéros calculés par lui vérifient tous l'hypothèse de Riemann ; on pourrait penser que cela signifie seulement qu'ils sont positionnés assez près de la droite critique (au sens où l'imprécision de calcul ne permettrait pas d'exclure qu'ils peuvent y être exactement) ; il n'en est rien, comme on va le voir. Cependant, si on a une certitude mathématique pour, mettons, les premiers millions de zéros, la complexité (y compris informatique) des calculs rend plus relative la confiance qu'on peut avoir dans les derniers résultats ; cette question est soigneusement analysée par Xavier Gourdon 2004 (page 3, et plus précisément section 3.3.1) où il annonce le record de vérification des 1013 premiers zéros (et des tests statistiques sur des zéros bien plus éloignés encore).
Les méthodes de vérification numérique partent le plus souvent de la remarque selon laquelle la fonction : a les mêmes zéros que zêta dans la bande critique, et qu'elle est réelle sur la droite critique (à cause de l'équation fonctionnelle vue plus haut reliant et ). Il est alors facile de montrer l'existence d'au moins un zéro entre deux points de cette droite en vérifiant numériquement que cette fonction a des signes opposés en ces deux points. En pratique, on utilise la fonction Z (en) de Hardy et la fonction θ de Riemann-Siegel, avec : ; en déterminant de nombreux intervalles dans lesquels Z change de signe, on montre l'existence du même nombre de zéros sur la ligne critique. Pour contrôler l'hypothèse de Riemann jusqu'à une partie imaginaire T donnée, il reste à démontrer qu'il n'y a pas d'autres zéros dans cette région ; il suffit pour cela de calculer le nombre total de zéros dans la région en question (le rectangle de sommets 0,1, iT et 1+iT), ce qui peut se faire en appliquant le théorème des résidus à la fonction 1/ζ (techniquement, le problème d'éventuels zéros doubles fait qu'on utilise en réalité la fonction ζ'/ζ, même si une autre conjecture est qu'il n'en existe pas) : comme ce nombre doit être entier, un calcul numérique suffisamment précis de l'intégrale appropriée donne une certitude. La table suivante recense les calculs effectués jusqu'ici (lesquels, bien sûr, ont tous confirmé l'hypothèse) et donne des indications sur les méthodes utilisées.
| Année | Nombre de zéros | Auteurs et méthodes utilisées |
|---|---|---|
| 1859? | 3 | B. Riemann utilise la formule de Riemann-Siegel (non publié, mais cité par Siegel 1932). |
| 1903 | 15 | J. P. Gram 1903 utilise la formule d'Euler-Maclaurin et découvrit la loi de Gram. Il montre que les 10 zéros de partie imaginaire inférieure à 50 sont sur la droite critique en calculant la somme des puissances 10-èmes des zéros qu'il a trouvés. |
| 1914 | 79 (γn ≤ 200) | R. J. Backlund 1914 introduit une meilleure méthode de contrôle, en étudiant l'argument S(T) de la fonction zêta. |
| 1925 | 138 (γn ≤ 300) | J. I. Hutchinson 1925 découvre la première exception à la loi de Gram, au point de Gram g126. |
| 1935 | 195 | E. C. Titchmarsh 1935 utilise la formule de Riemann-Siegel, qui vient d'être redécouverte, et qui est beaucoup plus rapide que la formule sommatoire d'Euler : il faut environ O(T3/2+ε) étapes pour tester des zéros de partie imaginaire inférieure à T, alors que la méthode d'Euler-Maclaurin prend environ O(T2+ε) étapes. |
| 1936 | 1041 | E. C. Titchmarsh 1936 et L. J. Comrie sont les derniers à calculer des zéros à la main. |
| 1953 | 1104 | A. M. Turing 1953 trouve une méthode plus efficace pour contrôler l'absence de zéros en dehors de la droite critique jusqu'à la hauteur T, en vérifiant que Z a le signe correct en plusieurs points de Gram consécutifs, et en utilisant le fait que S(T) est de valeur moyenne 0. Cela ne demande presque aucun calcul supplémentaire, car le signe de Z aux points de Gram est déjà connu ; cette méthode est toujours la plus fréquemment utilisée. Ce calcul est le premier à avoir été effectué par un ordinateur. |
| 1956 | 15000 | D. H. Lehmer 1956 découvre quelques cas de zéros « tout juste » sur la ligne : deux zéros sont si proches qu'il est difficile de montrer un changement de signe entre eux. Ceci est appelé le « phénomène de Lehmer », et se produit pour la première fois aux zéros de partie imaginaire 7005,063 et 7005,101, qui diffèrent de seulement 0,04, alors que l'écart moyen entre d'autres zéros dans cette région est de l'ordre de 1. |
| 1956 | 25000 | D. H. Lehmer |
| 1958 | 35337 | N. A. Meller |
| 1966 | 250000 | R. S. Lehman |
| 1968 | 3500000 | Rosser, Yohe et Schoenfeld 1969 énoncent la règle de Rosser (voir plus bas). |
| 1977 | 40000000 | R. P. Brent |
| 1979 | 81000001 | R. P. Brent |
| 1982 | 200000001 | R. P. Brent, J. van de Lune, H. te Riele, D. T. Winter |
| 1983 | 300000001 | J. van de Lune, H. te Riele |
| 1986 | 1500000001 | van de Lune, te Riele et Winter 1986 donnent des informations statistiques sur la répartition des zéros, et déterminent plusieurs graphes de Z en des points où son comportement est inattendu. |
| 1987 | Quelques zéros à de grandes hauteurs | A. M. Odlyzko 1987 calcule, avec une grande précision, un nombre beaucoup plus petit de zéros, mais à des hauteurs T de l'ordre de 1012, pour tester la conjecture de Montgomery sur les corrélations entre paires de zéros. |
| 1992 | Quelques zéros à de grandes hauteurs | A. M. Odlyzko 1992 calcule quelques autres zéros à des hauteurs allant jusqu'à 1020, accompagnés d'une discussion approfondie des résultats. |
| 2001 | 10000000000 | J. van de Lune (non publié) |
| 2004 | 900000000000 | S. Wedeniwski (ZetaGrid ; informatique répartie) |
| 2004 | 10000000000000 | Xavier Gourdon 2004 et Patrick Demichel utilisent l'algorithme d'Odlyzko-Schönhage. Ils vérifient également quelques zéros à des hauteurs bien plus grandes. |
Essais de démonstration
modifierDes approches directes ayant régulièrement échoué, plusieurs lignes d'attaque plus élaborées ont été proposées. Il est d'abord possible de transformer l'hypothèse en termes de théorie des nombres ; on montre par exemple que plusieurs conjectures, comme la conjecture de Mertens, entraîneraient l'hypothèse de Riemann (on dit qu'elles sont plus fortes). Malheureusement, cette approche n'a eu comme seul résultat que de réfuter, par exemple, la conjecture de Mertens.
Certaines conjectures analogues, à première vue plus générales, se sont paradoxalement révélées un peu plus faciles à démontrer. C'est le cas des conjectures de Weil, dans lesquelles la fonction zêta est remplacée par les fonctions L : elles ont été démontrées par Pierre Deligne en 1974 à l'aide des puissants outils de géométrie algébrique développés par Alexandre Grothendieck, mais cette technique semble impossible à adapter au cas de la fonction zêta.
Une autre piste part d'étranges analogies entre la répartition empirique des zéros connus et le spectre de certains opérateurs ; là encore, il n'a pas été possible d'en tirer même un plan d'attaque.
En , une percée jugée prometteuse[10] reprend un résultat de 1927 dû à George Pólya qui relie l'hypothèse à une propriété des zéros de certains polynômes (les polynômes de Jensen) ; Ken Ono, Don Zagier et deux autres chercheurs démontrent cette propriété pour une vaste classe de polynômes (insuffisante néanmoins pour résoudre le problème) par une approche complètement originale[11].
Arguments pour et contre l'hypothèse de Riemann
modifierLes articles mathématiques sur l'hypothèse de Riemann ont tendance à refuser prudemment de s'engager quant à sa vérité. Parmi les auteurs qui expriment une opinion, la plupart, comme Riemann lui-même[12] et Bombieri[1] laissent entendre qu'ils s'attendent à ce qu'elle soit vraie, ou du moins qu'ils l'espèrent. Quelques auteurs expriment de sérieux doutes à son sujet, comme Ivić[13], qui énumère quelques raisons à son scepticisme, et Littlewood[14], qui déclare carrément qu'il la croit fausse et qu'il n'y a aucune raison imaginable pour qu'elle soit vraie. Les articles de synthèse s'accordent à dire que les preuves sont fortes mais pas accablantes, de sorte que, même si elle est probablement vraie, il existe un doute raisonnable ; ils listent à ce sujet les arguments suivants[1],[15],[16],[13] :
- Plusieurs résultats analogues ont été démontrés ; la démonstration des conjectures de Weil par Deligne[17] (correspondant au cas des variétés sur un corps fini) est peut-être la plus forte raison théorique en faveur de l’hypothèse, et donne des raisons d’espérer que soit vraie une conjecture plus générale, portant sur les fonctions analogues associées à des formes automorphes. De même, des analogues de l’hypothèse de Riemann sont vraies pour les fonctions zêta de Selberg, et pour la fonction zêta de Goss. En revanche, certaines fonctions zêta d'Epstein (en) ne la vérifient pas, mais ces fonctions ont moins d’analogies avec la fonction de Riemann, n’ayant pas de produit eulérien ni de relations avec des formes automorphes[18].
- Il semblerait à première vue que la vérification numérique de ce que tous les zéros jusqu’à une hauteur T de sont sur la droite critique est une forte confirmation de l’hypothèse. Mais en théorie analytique des nombres, il est souvent arrivé que des conjectures de ce genre soient réfutées, les premières exceptions se produisant pour des valeurs bien plus grandes que ce que permet de tester une approche directe, comme dans le cas de la conjecture ayant donné naissance au nombre de Skewes. Le problème vient de ce que le comportement de la fonction zêta à la hauteur T est influencé par des termes grandissant comme log log T, et tendant vers l'infini si lentement que le calcul ne permet pas de les détecter : ainsi, un terme correctif (noté généralement S(T) dans la littérature) augmenterait de 2 à chaque passage de zéros non sur la droite critique, or il se comporte en (log log T)1/2 et ne dépasse guère 3 partout où on a pu le calculer ; T devrait donc être supérieur à pour que l'on ait une chance, selon ce raisonnement, de voir apparaître des contre-exemples à la conjecture ; une telle hauteur est inaccessible au calcul avec nos méthodes actuelles.
- Arnaud Denjoy a donné un argument probabiliste en faveur de l'hypothèse de Riemann[19], basé sur la remarque selon laquelle si μ est une suite aléatoire de « 1 » et de « −1 », alors pour tout ε > 0, les sommes partielles (dont les valeurs sont les positions d'une marche aléatoire) satisfont presque sûrement . L'hypothèse de Riemann est équivalente à ce résultat pour la fonction de Möbius μ et pour la fonction de Mertens M correspondante ; en d'autres mots, l'hypothèse de Riemann est en un certain sens équivalente à dire que la fonction de Möbius se comporte comme une suite de tirages au sort à pile ou face, et compte tenu de la définition de cette fonction, à dire que la parité du nombre de facteurs premiers d'un entier se comporte au hasard. En théorie des nombres, des arguments de ce genre donnent souvent la bonne réponse, mais s'avèrent difficiles à rendre rigoureusement , et échouent parfois, comme dans le cas du théorème de Maier (en).
- Les calculs faits par Odlyzko[20] montrent que les zéros de la fonction zêta se comportent comme les valeurs propres d'une matrice hermitienne aléatoire, suggérant que ce pourraient être les valeurs propres d'un opérateur auto-adjoint (ce qui impliquerait l'hypothèse de Riemann). Cependant, toutes les tentatives de construire un tel opérateur ont échoué.
- Plusieurs théorèmes, comme la conjecture faible de Goldbach, d'abord démontrés à l'aide de l'hypothèse de Riemann (généralisée), furent par la suite démontrés inconditionnellement. Cela peut être considéré comme une indication de ce que l'hypothèse est vraie.
- L'existence de paires de Lehmer (en)[21] (deux zéros très proches) est parfois vue comme indication de ce que l'hypothèse est fausse. Mais cela se produirait même si elle était vraie, comme le montrent les calculs d'Odlyzko confirmant la conjecture de Montgomery (en).
- Samuel James Patterson (en) suggère que pour la plupart des mathématiciens, l'argument le plus fort en faveur de l'hypothèse est l'espoir que les nombres premiers soient distribués le plus régulièrement possible[22].
Pseudo-démonstrations
modifierDe nombreuses preuves supposées de l'hypothèse de Riemann sont régulièrement proposées, principalement sur Internet, ainsi que quelques infirmations, souvent le fait d'amateurs en marge du système universitaire traditionnel, mais parfois aussi de mathématiciens professionnels, mais s’éloignant de leur domaine d’expertise (les plus célèbres de ces dernières tentatives étant dues à Louis de Branges en 2004 et à Michael Atiyah en 2018). Aucun de ces travaux n'a pour le moment reçu l'assentiment de la communauté mathématique.
Le site du mathématicien britannique Matthew R. Watkins[23] recense quelques-unes de ces supposées preuves — y compris des « preuves » que l'hypothèse serait fausse —, en plus de quelques parodies.
Notes et références
modifier- (en) Enrico Bombieri, « The Riemann Hypothesis ».
- Le texte de Bombieri a été mis à jour en 2004 par Peter Sarnak : (en) Problems of the Millennium: The Riemann Hypothesis (2004), une analyse des travaux récents.
- Leonhard Euler. Variae observationes circa series infinitas. Commentarii academiae scientiarum Petropolitanae 9, 1744, pp. 160-188, Théorèmes 7 et 8.
- Pour d'autres méthodes, voir Fonction zêta de Riemann#Extension à ℂ-{1}.
- Mais si 0 < Re(s) < 1, la convergence (évidemment non absolue) est excessivement lente ; cette série, sous cette forme, ne permet absolument pas le calcul numérique de zêta ; il est heureusement possible de la transformer grâce à la formule d'Euler-Maclaurin pour obtenir une convergence rapide.
- Voir Fonction zêta de Riemann#Relation fonctionnelle pour une démonstration de cette identité.
- (en) Peter Borwein, The Riemann Hypothesis : A Resource for the Afficionado and Virtuoso Alike, Springer, (lire en ligne), p. 16.
- Le manuscrit original, sur le site du Clay Institute, et sa traduction en français par L. Laugel, sur wikisource.
- (en) Richard Bellman, A Brief Introduction of Theta Functions (Holt, 1961) p. 33-34
- (en) Enrico Bombieri, « New progress on the zeta function: From old conjectures to a major breakthrough », PNAS, (lire en ligne).
- (en) Michael Griffin, Ken Ono, Larry Rolen et Don Zagier, « Jensen polynomials for the Riemann zeta function and other sequences », PNAS, (lire en ligne).
- Article de Riemann : manuscrit, transcription en allemand et traduction en anglais.
- (en) Aleksandar Ivić, The Riemann Hypothesis: A Resource for the Afficionado and Virtuoso Alike, New York, Springer, coll. « CMS Books in Mathematics », (ISBN 978-0-387-72125-5, arXiv math.NT/0311162), « On some reasons for doubting the Riemann hypothesis », p. 131–160.
- (en) J. E. Littlewood, The scientist speculates: an anthology of partly baked idea, New York, Basic books, , « The Riemann hypothesis »
- (en) Peter Sarnak, « Problems of the Millennium: The Riemann Hypothesis (2004) », Institut de mathématiques Clay, (consulté le ).
- (en) J. B. Conrey, « More than two fifths of the zeros of the Riemann zeta function are on the critical line », J. Reine Angew. Math., vol. 1989, no 399, , p. 1–26 (DOI 10.1515/crll.1989.399.1, MR 1004130, S2CID 115910600, lire en ligne)
- Pierre Deligne, « La conjecture de Weil. I », Publications mathématiques de l'IHÉS, vol. 43, , p. 273–307 (DOI 10.1007/BF02684373, MR 0340258, S2CID 123139343, lire en ligne)
- (en) Edward Charles Titchmarsh, The theory of the Riemann zeta-function, The Clarendon Press Oxford University Press, (ISBN 978-0-19-853369-6, MR 882550)
- (en) H. M. Edwards, Riemann's Zeta Function, New York, Dover Publications, (ISBN 978-0-486-41740-0, MR 0466039)
- Odlyzko 1987.
- Lehmer 1956.
- (en) S. J. Patterson, An introduction to the theory of the Riemann zeta-function, vol. 14, Cambridge University Press, coll. « Cambridge Studies in Advanced Mathematics », (ISBN 978-0-521-33535-5, DOI 10.1017/CBO9780511623707, MR 933558), p. 75
- (en) Matthew R. Watkins, « proposed (dis)proofs of the Riemann Hypothesis », sur Exeter University's School of Engineering, Computing and Mathematics (consulté le )
Voir aussi
modifierBibliographie
modifier- (en) Albert E. Ingham, The Distribution of Prime Numbers, Cambridge University Press, Cambridge Tracts in Mathematics and Mathematical Physics vol. 30, . Réimpression 1990, (ISBN 978-0-521-39789-6).
- (en) Aleksandar Ivić, The Riemann Zeta Function, John Wiley & Sons, New York, , 517 p. (ISBN 978-0-471-80634-9) (Réimpression Dover 2003).
- (en) Edward Charles Titchmarsh, The theory of the Riemann zeta-function, The Clarendon Press Oxford University Press, , 412 p. (ISBN 978-0-19-853369-6, lire en ligne)
Ouvrages de vulgarisation
modifier- John Derbyshire (en), Dans la jungle des nombres premiers, Dunod, , 390 p. (ISBN 978-2-10-050046-8 et 2-10-050046-5) traduction de (en) John Derbyshire, Prime Obsession, Joseph Henry Press, Washington, DC, , 446 p. (ISBN 978-0-309-08549-6, lire en ligne)
- (en) Karl Sabbagh, The Riemann Hypothesis : The Greatest Unsolved Problem in Mathematics, Farrar, Straus and Giroux, (ISBN 0-374-52935-3).
- Rossana Tazzioli, Riemann, le géomètre de la nature, Belin (ISBN 978-2-84245-106-6 et 2-84245-106-6)
- Marcus du Sautoy (trad. de l'anglais), La Symphonie des nombres premiers, Paris, Éditions Héloïse d'Ormesson, 491 p. (ISBN 978-2-35087-011-3 et 2-35087-011-1)
Articles techniques
modifier- R. J. Backlund, « Sur les zéros de la fonction ζ(s) de Riemann », CRAS, vol. 158, , p. 1979–1981
- (en) X. Gourdon, « The 1013 first zeros of the Riemann zeta function, and zeros computation at very large height », une version consultable en ligne, , voir aussi (en) Computation of zeros of the zeta function
- J. P. Gram, « Note sur les zéros de la fonction ζ(s) de Riemann », Acta Mathematica, vol. 27, , p. 289–304 (DOI 10.1007/BF02421310)
- (en) J. I. Hutchinson (en), « On the Roots of the Riemann Zeta-Function », Trans. Amer. Math. Soc., vol. 27, no 1, , p. 49–60 (DOI 10.2307/1989163, JSTOR 1989163)
- (en) D. H. Lehmer, « Extended computation of the Riemann zeta-function », Mathematika. A Journal of Pure and Applied Mathematics, vol. 3, no 02, , p. 102–108 (DOI 10.1112/S0025579300001753, MR 0086083)
- (en) A. M. Odlyzko, « On the distribution of spacings between zeros of the zeta function », Mathematics of Computation, vol. 48, no 177, , p. 273–308 (DOI 10.2307/2007890, JSTOR 2007890, MR 866115)
- (en) A. M. Odlyzko, The 1020-th zero of the Riemann zeta function and 175 million of its neighbors, (lire en ligne)Ce livre non publié décrit l'implémentation de l'algorithme et discute les résultats de façon détaillée.
- (en) J. Barkley Rosser, J. M. Yohe et Lowell Schoenfeld (en), « Rigorous computation and the zeros of the Riemann zeta-function. (With discussion) », Information Processing 68 (Proc. IFIP Congress, Edinburgh, 1968), Vol. 1: Mathematics, Software, Amsterdam, North-Holland, , p. 70–76 (MR 0258245)
- (de) C. L. Siegel, « Über Riemanns Nachlaß zur analytischen Zahlentheorie », Quellen Studien zur Geschichte der Math. Astron. und Phys. Abt. B: Studien 2, , p. 45–80 Reprinted in Gesammelte Abhandlungen, Vol. 1. Berlin: Springer-Verlag, 1966
- (en) E. C. Titchmarsh, « The Zeros of the Riemann Zeta-Function », Proceedings of the Royal Society, Series A, Mathematical and Physical Sciences, vol. 151, no 873, , p. 234–255 (DOI 10.1098/rspa.1935.0146, JSTOR 96545)
- (en) E. C. Titchmarsh, « The Zeros of the Riemann Zeta-Function », The Royal Society, vol. 157, no 891, , p. 261–263 (DOI 10.1098/rspa.1936.0192, JSTOR 96692)
- (en) A. M. Turing, « Some calculations of the Riemann zeta-function », Proceedings of the London Mathematical Society, Third Series, vol. 3, , p. 99–117 (DOI 10.1112/plms/s3-3.1.99, MR 0055785)
- (en) J. van de Lune, H. te Riele et D. T. Winter, « On the zeros of the Riemann zeta function in the critical strip. IV », Mathematics of Computation, vol. 46, no 174, , p. 667–681 (DOI 10.2307/2008005, JSTOR 2008005, MR 829637)
Articles connexes
modifier- Analyse complexe
- Hypothèse de Riemann généralisée
- Histoire de la fonction zêta de Riemann
- Fonction zêta de Riemann
- Conjecture de Hilbert-Pólya
- Fonction R de Riemann
- Fonction zêta locale
Liens externes
modifier- (en) « Riemann Hypothesis », sur Clay Mathematics Institute
- Michel Balazard, « Un siècle et demi de recherches sur l'hypothèse de Riemann », Gazette des mathématiciens, vol. 126, , p. 7-24 (lire en ligne)
- Gilles Lachaud, « L'hypothèse de Riemann : le Graal des mathématiciens », Les Dossiers de La Recherche, no 20, , p. 26-35 (lire en ligne)
- Gérard Villemin, « Hypothèse de Riemann », sur Nombres - Curiosités, théorie et usages