Bicoupole

Ensemble des bicoupoles
Sommets	4n
Arêtes	8n
Faces	2n triangles, 2n carrés 2 n-gones
Groupe de symétrie	Ortho : Dnh
Groupe de symétrie	Gyro : Dnd
Propriétés	convexe

En géométrie, une bicoupole est un solide formé en connectant deux coupoles par leurs bases.

Le gyrobiprisme triangulaire (J26) peut être considéré comme une gyrobicoupole carrée.

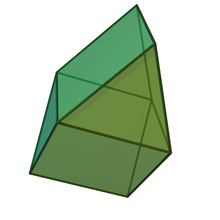
Il existe deux classes de bicoupoles parce que chaque moitié de coupole est bordée par une alternance de triangles et de carrés.

Si les faces identiques sont placées ensemble, le résultat est une orthobicoupole.

Si les faces sont différentes, c'est une gyrobicoupole.

Les coupoles et les bicoupoles existent en tant qu'ensembles infinis de polyèdres, comme les pyramides, les bipyramides, les prismes, les antiprismes et les trapèzoèdres.

Six bicoupoles ont des faces polygonales régulières : les orthobicoupoles hexagonales, octogonales et décagonales, ainsi que les gyrobicoupoles hexagonales, octogonales et décagonales La gyrobicoupole hexagonale est un solide d'Archimède, le cuboctaèdre; les cinq autres bicoupoles sont des solides de Johnson.

Les bicoupoles d'ordre plus élevé peuvent être construites si les faces sur le flanc sont autorisées à s'étirer en rectangles et en triangles isocèles.

Les bicoupoles ont quatre faces sur chaque sommet. Leurs polyèdres duaux ont donc tous des faces quadrilatérales. Le meilleur exemple connu est le dodécaèdre rhombique composé de 12 faces rhombiques. Le dual de la forme ortho, l'orthobicoupole hexagonale, est aussi un dodécaèdre, similaire au dodécaèdre rhombique, mais il possède 6 faces trapézoïdales dont les arêtes courtes et longues alternent autour de la circonférence.

Formes

Ensemble des orthobicoupoles :

	Orthobicoupole hexagonale (J27) : 8 triangles, 6 carrés ; son dual est le dodécaèdre trapézorhombique (en)
	Orthobicoupole octogonale (J28) : 8 triangles, 10 carrés
	Orthobicoupole décagonale (J30) : 10 triangles, 10 carrés, 2 pentagones
	Orthobicoupoles 2n-gonales : 2n triangles, 2n carrés, 2 n-gones

Ensemble de gyrobicoupoles :

	Gyrobicoupole hexagonale ou Cuboctaèdre : 8 triangles, 6 carrés ; son dual est le dodécaèdre rhombique
	Gyrobicoupole octogonale (J29) : 8 triangles, 10 carrés
	Gyrobicoupole décagonale (J31) : 10 triangles, 10 carrés, 2 pentagones
	Gyrobicoupoles 2n-gonales : 2n triangles, 2n carrés, 2 n-gones

Référence

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Bicupola (geometry) » (voir la liste des auteurs).