Approximation de Bernstein
En analyse, l'approximation de Bernstein est une méthode d'approximation polynomiale, permettant d'approcher uniformément une fonction continue f définie sur le segment [0, 1] par une suite de combinaisons linéaires des polynômes de Bernstein. Cette preuve constructive du théorème d'approximation de Weierstrass est due à Sergueï Natanovitch Bernstein[1].
Définition
modifierLa n-ième approximation de f est le polynôme
où les sont les polynômes de Bernstein :
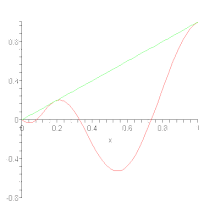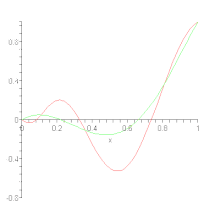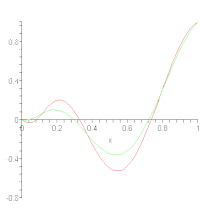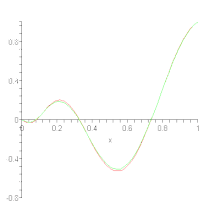
On construit donc Pn(f) à partir des valeurs de f aux points 0, 1⁄n, …, (n – 1)⁄n et 1 mais, en ces points, la valeur de Pn(f) peut être différente de celle de f, autrement dit : l'approximation obtenue n'est pas une interpolation.
La convergence uniforme de Pn(f) vers f s'énonce donc de la façon suivante :
Il convient de noter que si X est une variable aléatoire suivant une loi binomiale de paramètres(n,x), alors Pn(f)(x) n'est rien d'autre que l'espérance de f(X/n), c'est-à-dire la moyenne de f appliquée au nombre de succès de n expériences indépendantes de probabilité x. La convergence simple de Pn(f) vers f est alors une conséquence immédiate de la loi faible des grands nombres. En majorant la probabilité de l'écart entre X⁄n et x, on en déduit la convergence uniforme.
Démonstration
modifierLes opérateurs linéaires Pn sur C([0, 1]) étant positifs (en), il suffit, d'après le théorème d'approximation de Korovkin, de vérifier la convergence pour les trois fonctions monomiales f0(x) = 1, f1(x) = x et f2(x) = x2.
Or Pn(f0) = f0, Pn(f1) = f1 et Pn(f2) = f2 + (f1 – f2)/n, ce qui conclut[2].
Vitesse de convergence
modifierSoit f une fonction continue sur [0;1], et ω le module de continuité de f. Alors on a l'inégalité[3] :
Où représente la norme « infini ».
Ce résultat permet d'assurer une certaine vitesse de convergence de la suite de polynômes de Bernstein vers la fonction f, en fonction du module de continuité de f.
Références
modifier- « Démonstration du théorème de Weierstrass, fondée sur le calcul des probabilités », dans Comm. Soc. Math. Kharkov Ser. 2, vol. 13, 1912.
- (en) Francesco Altomare, « Korovkin-type Theorems and Approximation by Positive Linear Operators », Surveys in Approximation Theory, vol. 5, , p. 92-164 (arXiv 1009.2601), Theorem 3.6.
- (en) Michelle Schatzman, Numerical analysis: a mathematical introduction, Oxford University Press, 2002, Theorem 5.3.2
