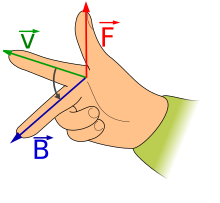
Vecteur de Poynting

En physique, le vecteur de Poynting est la densité de flux liée à la propagation de l'onde électromagnétique. Sa direction est la direction de propagation. On le note ${\vec {\Pi }}$, ${\vec {S}}$, ${\vec {R}}$ ou ${\vec {N}}$.

Vecteur de Poynting

Produit vectoriel du champ électrique V par le champ magnétique B.

Données clés

Unités SI	watt par mètre carré (W m−2)
Dimension	M·T −3
Nature	Grandeur vectorielle intensive
Symbole usuel	${\vec {S}}$, ${\vec {\Pi }}$, ${\vec {R}}$ ou ${\vec {N}}$
Lien à d'autres grandeurs	${\vec {\Pi }}$ = ${\frac {1}{\mu _{0}}}$ ${\vec {E}}$ $\wedge$${\vec {B}}$ ${\vec {\Pi }}$ ⋅ ${\vec {\mathrm {d} S}}$ $=\mathrm {d}$$\Phi _{\mathrm {e} }$

Le flux du vecteur de Poynting à travers une surface (fermée ou non) est égal à la puissance véhiculée par l'onde à travers cette surface. Le module de ce vecteur est donc une puissance par unité de surface, c'est-à-dire une densité de flux d'énergie ; il est homogène à un éclairement énergétique et à une exitance énergétique ; et, dans le Système international (SI) d'unités, il s'exprime en watts par mètre carré.

Histoire

L'éponyme du vecteur de Poynting est le physicien anglais John Henry Poynting (1852-1914) qui l'a introduit en 1884. Oliver Heaviside (1850-1925) l'a découvert quelques mois plus tard et de manière indépendante.

Définition

Le Vocabulaire électrotechnique international (VEI) définit le vecteur de Poynting ${\vec {\Pi }}$ comme le produit vectoriel du champ électrique ${\vec {E}}$ par le champ magnétique ${\vec {H}}$ du champ électromagnétique en un point donné :

${\vec {\Pi }}={\vec {E}}\wedge {\vec {H}}$.

L'expression ci-dessus est connue comme la forme d'Abraham.

Dans le vide, le champ magnétique ${\vec {H}}$ est en tout point égal au quotient de l'induction magnétique ${\vec {B}}$ par la constante magnétique $\mu _{0}$ :

${\vec {H}}={\frac {\vec {B}}{\mu _{0}}}$,

de sorte que, dans le vide, la définition précédente du vecteur de Poynting est équivalente à :

${\vec {\Pi }}={\vec {E}}\wedge {\frac {\vec {B}}{\mu _{0}}}$.

Par définition du produit vectoriel, le vecteur de Poynting est un vecteur axial, orthogonal aux deux vecteurs ${\vec {E}}$ et ${\vec {H}}$, tel que les trois vecteurs ${\vec {E}}$, ${\vec {H}}$ et ${\vec {\Pi }}$ forment un trièdre direct ou un trièdre rétrograde selon l'orientation de l'espace ; et la norme du vecteur de Poynting est égale au produit des normes des deux vecteurs et du sinus de leur angle :

$\|{\vec {\Pi }}\|=\|{\vec {E}}\|\cdot \|{\vec {H}}\|\cdot \sin \vartheta$.

Expression générale du vecteur de Poynting

Soient ${\vec {E}}$ et ${\vec {B}}$ le champ électrique et le champ magnétique. La conservation de l'énergie électromagnétique à travers une surface s'exprime, dans sa forme locale (souvent appelée théorème de Poynting), comme une équation de conservation :

${\frac {\partial e(t)}{\partial t}}+{\vec {\nabla }}\cdot {\vec {\Pi }}(t)=s(t)$

avec $t$ le temps, $e$ la densité volumique d'énergie du champ électromagnétique, ${\vec {\Pi }}$ le flux d'énergie surfacique sortant, et $s$ le terme source : la densité volumique d'énergie gagnée $s>0$ ou perdue.

À partir des équations de Maxwell dans le vide, on tire l'expression du vecteur de Poynting dans le vide :

${\vec {\Pi }}(t)={\frac {{\vec {E}}(t)\wedge {\vec {B}}(t)}{\mu _{0}}}$

où μ₀ est la perméabilité du vide.

Dans un matériau linéaire, de perméabilité magnétique μ et dans lequel on peut négliger la dispersion et les pertes, il convient de prendre en compte l'excitation magnétique ${\vec {H}}(t)$ définie par la relation ${\vec {B}}(t)=\mu \,{\vec {H}}(t)$. On obtient alors une expression plus générale du vecteur de Poynting :

${\vec {\Pi }}(t)={\vec {E}}(t)\wedge {\vec {H}}(t)$.

Dans un milieu linéaire dispersif avec pertes, on conserve l'expression du vecteur de Poynting ${\vec {\Pi }}={\vec {E}}\wedge {\vec {H}}$, mais le théorème de Poynting ne s'exprime plus avec $e$ et comporte des termes supplémentaires de dissipation.

Moyenne temporelle en notation complexe

Un circuit de courant continu constitué d'une batterie (V) et d'une résistance (R) indiquant la direction du vecteur de Poynting (S, bleu) dans l'espace qui l'entoure, ainsi que les champs desquels il est dérivé : le champ électrique (E, rouge) et le champ magnétique (H, vert). Dans la région autour de la batterie le vecteur Poynting est dirigé vers l'extérieur, ce qui indique la puissance sortant de la batterie dans les champs; dans la région autour de la résistance le vecteur est dirigé vers l'intérieur, ce qui indique la puissance de champ circulant dans la résistance. À travers n'importe quel plan P, entre la batterie et la résistance, le flux de Poynting est dans le sens de la résistance.

Dans le cas d'une onde électromagnétique plane progressive harmonique, on a

${\vec {E}}={\vec {E}}_{0}\cos {(\omega t-\varphi )}$

et

${\vec {B}}={\vec {B}}_{0}\cos {(\omega t-\psi )}$

On peut donc associer des grandeurs complexes aux champs ${\vec {E}}$ et ${\vec {B}}$ en posant (avec $i$ le nombre complexe tel que $i^{2}=-1$) :

${\underline {\vec {E}}}={\underline {\vec {E}}}_{0}\,\mathrm {e} ^{i\omega t}={\vec {E}}_{0}\,\mathrm {e} ^{-i\varphi }\,\mathrm {e} ^{i\omega t}$

et

${\underline {\vec {B}}}={\underline {\vec {B}}}_{0}\mathrm {e} ^{i\omega t}={\vec {B}}_{0}\,\mathrm {e} ^{-i\psi }\,\mathrm {e} ^{i\omega t}$.

La moyenne temporelle du vecteur de Poynting vaut alors :

$\langle {\vec {\Pi }}\rangle ={\frac {1}{2\,\mu _{0}}}\;{\text{Re}}\left({\underline {\vec {E}}}\wedge {\underline {\vec {B}}}^{\star }\right)$

où ${\underline {\vec {B}}}^{\star }$ désigne le conjugué de ${\underline {\vec {B}}}$

Lien avec l'approche énergétique de la propagation d'un faisceau

La moyenne temporelle du flux de Poynting est reliée à la luminance $L(\Omega )$ d'un faisceau se propageant dans la direction $\Omega _{0}={\frac {\vec {\Pi }}{||{\vec {\Pi }}||}}$. Cette luminance est donnée par :

$L(\Omega )=\langle {\vec {\Pi }}\rangle \delta (\Omega -\Omega _{0})$

où $\delta$ est la distribution de Dirac.

On vérifie que le premier moment de $L(\Omega )$ qui représente la densité de flux ${\vec {f}}$ retrouve le flux de Poynting :

${\vec {f}}=\int _{S^{2}}\Omega L(\Omega )\mathrm {d} \Omega =\langle {\vec {\Pi }}\rangle$

Puissance électromagnétique traversant une surface

Une conséquence du théorème de Poynting est que la puissance électromagnétique traversant une surface S est donnée par le flux du vecteur de Poynting à travers cette surface.

${\mathcal {P}}_{S}=\iint _{S}{\vec {\Pi }}\cdot \mathrm {d} {\vec {S}}$

Équation de l'énergie d'un champ électromagnétique

Soit $U_{em}$ l'énergie du champ électromagnétique :

$U_{em}=\iiint _{V}W_{em}\mathrm {d} \tau$

avec W densité volumique d'énergie (quantité d'énergie par unité de volume)

On définit la quantité d'énergie quittant un volume $V$ pendant un temps $\mathrm {d} t$  :

$-{\frac {\mathrm {d} U_{em}}{\mathrm {d} t}}=-{\frac {\mathrm {d} }{\mathrm {d} t}}\iiint _{V}W_{em}\mathrm {d} \tau =-\iiint _{V}{\frac {\partial W_{em}}{\partial t}}\mathrm {d} \tau$

Soit ${\vec {P}}$, vecteur flux d'énergie du champ. D'après le théorème de Green-Ostrogradsky (Théorème de flux-divergence), on peut dire que le flux sortant du volume V est :

$\iint _{\Sigma }{\vec {P}}\cdot {\vec {n}}\ \mathrm {d} \sigma$

avec ${\vec {n}}$ un vecteur unitaire normal à la surface $\Sigma$ du volume V, orienté de l'intérieur vers l'extérieur.

On peut expliciter la perte d'énergie du volume de la manière suivante :

• pertes dues aux « frottements » des charges mobiles (voir loi Ohm locale, effet Joule) ;
• pertes dues au rayonnement électromagnétique sortant du volume.

On peut donc dire que :

$-\iiint _{V}{\frac {\partial W_{em}}{\partial t}}\mathrm {d} \tau =\iiint _{V}{\vec {\nabla }}\cdot {\vec {P}}\mathrm {d} \tau$ + travail fourni par le champ à la matière

On calcule ce travail :

${\vec {F}}_{\rm {{\acute {e}}lectrique}}=q({\vec {E}}+{\vec {v}}\wedge {\vec {B}})$.

Pour une particule :

$\mathrm {d} {\vec {W}}={\vec {F}}\cdot \mathrm {d} {\vec {r}}=q{\vec {E}}\cdot \mathrm {d} {\vec {r}}$ (on observe facilement que la force magnétique ne travaille pas).

On calcule maintenant la puissance fournie par le champ. La puissance reçue par une particule est :

${\vec {F}}\cdot {\vec {v}}=q\,{\vec {E}}\cdot {\vec {v}}$

La densité particulaire est notée $N$, en conséquence :

${\frac {\partial W_{Electrique}}{\partial t}}=Nq{\vec {E}}\cdot {\vec {v}}$ or $Nq{\vec {v}}={\vec {j}}$

donc ${\frac {\partial W_{Electrique}}{\partial t}}={\vec {j}}\cdot {\vec {E}}$

Cette perte de puissance est égale à la perte d'énergie du champ par unité de temps et de volume donc on écrit finalement :

$-\iiint _{V}{\frac {\partial W_{em}}{\partial t}}d\tau =\iiint _{V}{\vec {\nabla }}\cdot {\vec {P}}\mathrm {d} \tau +\iiint _{V}{\vec {j}}\cdot {\vec {E}}\mathrm {d} \tau$

Donc finalement on a :

$-{\frac {\partial W_{em}}{\partial t}}={\vec {\nabla }}\cdot {\vec {P}}+{\vec {j}}\cdot {\vec {E}}$

qui correspond à l'équation de l'énergie du champ électromagnétique.

Voir aussi

Bibliographie

• [Andrade Martins 2005] (en) Roberto de Andrade Martins, « Mechanics and electromagnetism in the late nineteenth century : the dynamics of Maxwell's ether », dans Marco Mamone Capria (éd.), Physics before and after Einstein, Amsterdam, IOS Press, hors coll., avril 2005, 1^re éd., VII-324 p., 16,5 × 25,4 cm (ISBN 1-58603-462-6, EAN 9781586034627, OCLC 493266942, BNF 41094146, SUDOC 088922537, présentation en ligne), chap. 2, p. 21-48 (OCLC 539623579, DOI 10.3233/978-1-58603-462-7-21, lire en ligne [PDF]).
• [Heaviside 1885] (en) Oliver Heaviside, « Electromagnetic induction and its propagation : on the transmission of energy through wires by the electric current », The Electrician, vol. 14,‎ 10 janvier 1885, p. 178-181 (lire en ligne).
• [Poynting 1884] (en) John Henry Poynting, « On the transfer of energy in the electromagnetic field » [« Sur le transfert d'énergie dans le champ électromagnétique »], Philos. Trans. R. Soc., vol. 175,‎ déc. 1884, art. n^o XV, p. 343-361 (OCLC 6067266495, DOI 10.1098/rstl.1884.0016, JSTOR 109449, Bibcode 1884RSPT..175..343P, résumé, lire en ligne [PDF]) — art. reçu le 17 déc. 1883 et lu le 10 janv. 1884.
• [Dubesset 2000] Michel Dubesset (préf. de Gérard Grau), Le manuel du Système international d'unités : lexique et conversions, Paris, Technip, coll. « Publications de l'Institut français du pétrole », sept. 2000, 1^re éd., 1 vol., XX-169, ill., fig. et tabl., 15 × 22 cm, br. (ISBN 2-7108-0762-9, EAN 9782710807629, OCLC 300462332, BNF 37624276, SUDOC 052448177, présentation en ligne, lire en ligne), s.v. vecteur de Poynting, p. 121.
• [Kaplan 2012] (en) Alexander E. Kaplan, « Gradient marker : a universal wave pattern in an inhomogeneous continuum », Physical Review Letters, vol. 109, n^o 15,‎ octobre 2012, article n^o 153901 (OCLC 815455228, DOI 10.1103/PhysRevLett.109.153901, Bibcode 2012PhRvL.109o3901K, arXiv 1207.6807, résumé, lire en ligne [PDF]).
• [Kinsler, Favaro et McCall 2009] (en) Paul Kinsler, Alberto Favaro et Martin W. McCall, « Four Poynting theorems », European Journal of Physics, vol. 30, n^o 5,‎ septembre 2009, p. 983-993 (OCLC 444711487, DOI 10.1088/0143-0807/30/5/007, Bibcode 2009EJPh...30..983K, arXiv 0908.1721, résumé, lire en ligne [PDF]).
• [Picon et Poulichet 2010] Odile Picon et Patrick Poulichet, Électromagnétisme, Paris, Dunod et l'Usine nouvelle, coll. « Aide-mémoire », octobre 2010, X-397 p., 13 × 18 cm (ISBN 978-2-10-054551-3, EAN 9782100545513, OCLC 708365621, BNF 42303925, SUDOC 147499623, présentation en ligne, lire en ligne).
• [Rabinowitz 2015] (en) Mario Rabinowitz, « General derivation of mass-energy relation without electrodynamics or Einstein's postulates », Journal of Modern Physics, vol. 6, n^o 9,‎ août 2015, p. 1243-1248, article n^o 58717 (DOI 10.4236/jmp.2015.69129, résumé, lire en ligne [PDF]).
• [Taillet, Villain et Febvre 2018] Richard Taillet, Loïc Villain et Pascal Febvre, Dictionnaire de physique, Louvain-la-Neuve, De Boeck supérieur, hors coll., janvier 2018, 4^e éd. (1^re éd. mai 2008), X-956 p., 17 × 24 cm (ISBN 978-2-8073-0744-5, EAN 9782807307445, OCLC 1022951339, BNF 45646901, SUDOC 224228161, présentation en ligne, lire en ligne).

Article connexe

• Théorème de Poynting

Liens externes

• [VEI] (en + fr) Commission électrotechnique internationale, Electropedia (vocabulaire électrotechnique international (VEI) en ligne) :
  • (en + fr) « vecteur de Poynting », VEI : 121-11-66 = 705-02-09 , octobre 2019. 
  • (en + fr) « vecteur de Poynting complexe », VEI : 705-02-10 , septembre 1995
  • (en + fr) « champ magnétique, excitation magnétique », VEI : 121-11-56 , août 1998. 
  • (en + fr) « produit vectoriel », VEI : 102-03-36 , août 2008. 
• (en) Jianqiu Zhang et Ke Cheng, « Poynting vector – an overview », sur ScienceDirect.
• [OI] (en) « Poynting vector » [« vecteur de Poynting »], notice d'autorité n^o 20110803100341357 de l'Oxford Index (OI), dans la base de données Oxford Reference de l'Oxford University Press (OUP).
• Notices d'autorité :

  • GND
• Notices dans des dictionnaires ou encyclopédies généralistes :

  • Britannica
  • Den Store Danske Encyklopædi