Trie (informatique)

En informatique, un ou une trie (prononcé [ˈtriː] ou [ˈtraɪ]) ou arbre préfixe, est une structure de données ayant la forme d'un arbre enraciné. Il est utilisé pour stocker une table associative où les clés sont généralement des chaînes de caractères. Contrairement à un arbre binaire de recherche, aucun nœud dans le trie ne stocke la chaîne à laquelle il est associé. C'est la position du nœud dans l'arbre qui détermine la chaîne correspondante.

Un trie pour les clés "A", "to", "tea", "ten", "ted", "i", "in", et "inn".

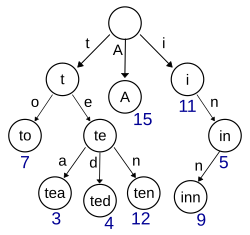
Pour tout nœud, ses descendants ont en commun le même préfixe. La racine est associée à la chaîne vide. Des valeurs ne sont pas attribuées à chaque nœud, mais uniquement aux feuilles et à certains nœuds internes se trouvant à une position qui désigne l'intégralité d'une chaîne correspondant à une clé.

Le terme de trie vient de l'anglais retrieval, signifiant extraction, recherche.

Origine

Les tries ont été décrits pour la première fois par l'américain René de la Briandais en 1959. Le terme trie a été inventé deux ans plus tard par Edward Fredkin, qui le prononce [ˈtriː], d’après la deuxième syllabe du mot anglais “retrieval”. Cependant beaucoup d'auteurs anglophones le prononcent [ˈtraɪ] (comme “try”), afin de le distinguer oralement de “tree”.

Applications

Les applications d'un trie sont nombreuses.

Cette structure de données peut servir à implémenter un tableau associatif ou un set, à trouver des redondances dans certains algorithmes de compression (par exemple dans les algorithmes de compression par dictionnaire à fenêtre glissante comme LZ77).

Les structures de données de type trie sont très souvent utilisé pour la saisie prédictive ou l'auto-complétion de texte, et plus généralement, dans beaucoup d'algorithmes de recherche approximative. Les tries rendent les recherches plus rapides, occupent moins d'espaces, spécialement quand l'ensemble des données est composés de chaines de caractères courtes, ce qui est le cas pour un correcteur orthographique ou syntaxique, pour faire des césures dans un éditeur de texte, ou encore, pour les algorithmes de recherche de préfixe long dans les routeurs .

Cependant, si le stockage des mots du dictionnaire est tout ce qui est requis (càd. qu'il n'est pas nécessaire de stocker de métadonnées associées à chaque mot), un automate à états finis acyclique déterministe minimal (DAFSA) (en) ou un arbre radix utilise moins d'espace de stockage qu'un trie. En effet, les DAFSA et les arbres radix peuvent compresser des branches identiques du trie qui correspondent aux mêmes suffixes (ou parties) de différents mots stockés. Les dictionnaires de chaînes sont également utilisés dans le traitement du langage naturel, comme la recherche du lexique d'un corpus.

Variantes

Il existe de nombreuses variantes de trie, parmi lesquelles :

• l'arbre préfixe, qu'on appelle souvent « trie » sans plus de précision ;
• l'arbre suffixe, qui stocke tout simplement les clefs dans l'autre sens ;
• l'arbre radix, arbre PATRICIA ou arbre crit-bit qui est plus compact en mémoire en regroupant plusieurs nœuds d'un trie équivalent en un seul.

Notes et références

Références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Trie » (voir la liste des auteurs).

Bibliographie

• (en) Edward Fredkin (en), « Trie Memory », dans Communications of the ACM, vol. 3, n° 9, septembre 1960, p. 490-499
• Alexandre Guidet, Programmation Objet en langage C++, Éditions Ellipses, (ISBN 978-2-7298-3693-1), 364 pages
• Bjarne Stroustrup, Le langage C++ - 4^e édition, Éditions Pearson Education France, 2003, (ISBN 978-2-7440-7003-7), 1098 pages
• Article sur les arbres sur developpez.com