Théorie des vagues d'Elliott

La théorie des vagues d'Elliott est une méthode d'analyse technique développée par Ralph Nelson Elliott dans les années 1930, utilisée pour prévoir les fluctuations des marchés financiers. Selon cette théorie, les mouvements de prix des actions suivent des motifs répétitifs, qu'Elliott appelle « vagues », qui reflètent la psychologie collective des investisseurs, traduisant les cycles d'optimisme et de pessimisme dans les comportements de marché. Ce modèle propose que les fluctuations ne soient pas aléatoires, mais qu'elles suivent des schémas récurrents, influencés par les tendances haussières et baissières du marché.

Les vagues d'Elliott simplifiées (à gauche) et dans un modèle plus réaliste (à droite) : la courbe est prise dans un canal haussier, se compose de trois vagues impulsives (montantes, 1, 3 et 5) et de deux vagues correctives (descendantes, 2 et 4), puis perce son canal (ici vers le bas, mais cela peut être vers le haut ou le bas).

La théorie repose sur deux types de vagues : les vagues impulsives et les vagues correctives. Les vagues impulsives suivent la tendance dominante, tandis que les vagues correctives s'y opposent. Ce modèle se compose de trois vagues impulsives et de deux vagues correctives, formant ainsi un cycle complet. Chaque vague elle-même peut être décomposée en sous-vagues, permettant d'analyser les marchés financiers à plusieurs échelles de temps. Ces cycles s'appliquent aussi bien aux tendances à court terme qu'aux mouvements de long terme, offrant ainsi un cadre d'analyse flexible pour les investisseurs.

Depuis la publication de The Wave Principle en 1938, la théorie des vagues d’Elliott est devenue un outil essentiel pour de nombreux analystes techniques. Bien qu'elle soit complexe et requière une compréhension approfondie des comportements de marché, elle reste influente dans les milieux financiers, en particulier pour ceux qui cherchent à prévoir les cycles économiques. Cependant, son interprétation subjective et sa précision font l'objet de débats parmi les experts financiers, certains voyant la théorie davantage comme un guide qu'une méthode infaillible.

Fondation

Le principe des vagues d'Elliott postule que la psychologie collective des traders, une forme de psychologie des foules, oscille entre optimisme et pessimisme en séquences répétées d'intensité et de durée. Ces fluctuations d'humeur créent des motifs dans les mouvements de prix des marchés à chaque degré de tendance ou échelle de temps.

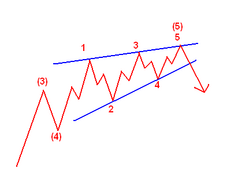
Selon la théorie d'Elliott, les marchés traversent deux phases : une phase motrice (impulsive), où les prix évoluent dans la direction de la tendance principale, et une phase corrective, où les prix évoluent à contre-courant de la tendance. Les impulsions sont toujours subdivisées en un ensemble de cinq vagues de degré inférieur, alternant à nouveau entre caractère motrice et correctif, de sorte que les vagues 1, 3, et 5 sont des impulsions, et les vagues 2 et 4 sont des retracements plus petits des vagues 1 et 3 respectivement. Les vagues correctives se subdivisent en trois vagues de degré inférieur commençant par une impulsion contre-tendance de cinq vagues, un retracement, et une autre impulsion. Dans un marché baissier, la tendance dominante est à la baisse, et le motif est inversé - cinq vagues à la baisse et trois à la hausse. Les vagues motrices évoluent toujours avec la tendance, tandis que les vagues correctives évoluent à contre-courant.

Éléments

1^er élément

Le mouvement complet est composé de 5 vagues. 3 de ces vagues sont dans la direction du mouvement, et deux vagues sont dans la direction contraire. La première, troisième, et cinquième vagues représentent la forme impulsive, la deuxième et la quatrième vague la forme corrective.

2^e élément

Les cinq vagues d'une dimension deviennent une seule vague d'une dimension d'un degré supérieur. A contrario, une seule vague d'une dimension est composée de 5 sous-vagues d'une dimension d'un degré inférieur.

3^e élément

Chaque vague impulsive (1-3-5) est composée de 5 sous-vagues, alors que chaque vague corrective (2-4) est composée de 3 sous-vagues.

Bien sûr, les travaux d'Elliott et leurs développements postérieurs ne se limitent pas à une simple affirmation péremptoire de cette situation mais énoncent des règles précises concernant la personnalité, la forme et la taille des différentes vagues.

Les règles

La vague 2 peut corriger jusqu'à 100 % la vague 1 mais ne peut en aucun cas, aller au-dessous de celle-ci. Il faut alors faire un nouveau comptage.

La vague 3 n'est jamais la vague la plus courte (en amplitude et non en durée). Si elle est plus petite, que la vague 1, alors la vague 5 sera encore plus petite que la 3. Cela ne souffre d'aucune exception.

La vague 4 ne peut jamais descendre plus bas que le sommet de la vague 1. Une seule exception est identifiable : les vagues 1 à 5 s’inscrivent dans une « ending diagonal ».

La personnalité des vagues

L'influence de la théorie de Charles Dow est ici déterminante. Elliott s'en inspire et la complète pour définir la personnalité des vagues, notamment celle de correction. Robert Prechter ira encore plus loin puisqu'il justifiera l'existence de ces vagues par la psychologie des différents types d'intervenants sur le marché.

À partir de R.N. Elliott's essay, "The Basis of the Wave Principle," October 1940.

La vague 1

Les vagues 1 sont difficiles à reconnaître puisqu'elles peuvent être interprétées comme de simples corrections faisant partie du précédent marché. Elles sont généralement très courtes et rapide. Il arrive fréquemment qu'on ne puisse décomposer la vague 1 qu'en trois vagues et non en 5. Cette vague est la vague des « astucieux » selon la théorie de Dow qui considérait que ceux-ci avaient accès à des informations avant les autres. On peut aussi dire que c'est la vague des contrariants qui achètent quand le marché baisse et vendent quand il monte.

La vague 2

Elle corrige généralement la première vague de façon considérable et entraînent souvent à penser que le mouvement précédent n'est pas encore terminé (fin de vague C). Des vagues 2 qui corrigent totalement les vagues 1 ne sont pas choses rares : on observe alors une configuration en double bottom s'il s'agit d'un mouvement haussier ou en double top dans le cas d'un mouvement baissier.

La vague 3

C'est la vague des « suiveurs ». Elle est la principale vague du mouvement. Une règle élémentaire à retenir concernant ce type de vague est qu'elle n'est jamais la plus courte parmi les vagues d'impulsion que sont les vagues 1, 3 et 5. Ce sont des vagues qui connaissent généralement des extensions et qui sont accompagnés de très forts volumes.

La vague 4

C'est une vague beaucoup moins violente que la vague 2. Elle vient consolider le marché. Selon le principe d'alternance (cf. infra), cette vague est donc souvent complexe : structure en plusieurs vagues et souvent en triangle. Une règle à retenir : une vague 4 ne cassera jamais le niveau atteint par le marché en fin de vague 1.

La vague 5

C'est la vague des petits porteurs. Elle est généralement peu dynamique mais elle dure assez longtemps. C'est la dernière phase d'un mouvement : la fin de l'euphorie pour les mouvements haussiers et du désespoir pour les mouvements baissiers. En fin de vague 5, on constate une baisse des volumes et parfois une vague 5 qui ne dépasse pas le top ou le bottom (selon que le marché est haussier ou baissier) de la vague 3.

La vague A

Elles sont parfois considérées comme des corrections techniques et non comme le début de la fin du mouvement.

La vague B

Elles retrouvent parfois le top (cas d'un mouvement haussier) de la vague 5 pour former un double-top.

La vague C

Elles viennent fermer la séquence de huit vagues de la théorie d'Elliott. Ce sont des vagues qui ressemblent aux vagues 3 en ampleur. Leurs similitudes conduisent d'ailleurs à de fréquentes confusions : est-on dans un marché véritablement baissier ou dans une simple phase de correction ?

Reconnaissance des motifs et fractales

La théorie d'Elliott repose sur l'analyse des graphiques de prix pour identifier des motifs de vagues, qui sont de nature fractale, ce qui signifie qu'ils se répètent sur différentes échelles de temps, et discerner ce que les prix pourraient faire ensuite ; ainsi, l'application du principe des vagues est une forme de reconnaissance de formes.

Les structures qu'Elliott a décrites répondent à la définition commune d'une fractale (motifs auto-similaires apparaissant à chaque degré de tendance). Les praticiens des vagues d'Elliott soutiennent que, tout comme les fractales naturelles s'étendent et deviennent plus complexes avec le temps, le modèle montre que la psychologie humaine collective se développe en motifs naturels, via des décisions d'achat et de vente reflétées dans les prix du marché : « C'est comme si nous étions d'une manière ou d'une autre programmés par les mathématiques. Coquillage, galaxie, flocon de neige ou humain : nous sommes tous liés par le même ordre ». Cependant, les critiques soutiennent qu'il s'agit d'une forme de paréidolie.

Règles et directives des vagues

Un comptage correct des vagues d'Elliott doit observer trois règles :

• La vague 2 ne retrace jamais plus de 100% de la vague 1.
• La vague 3 ne peut pas être la plus courte des trois vagues impulsives, à savoir les vagues 1, 3 et 5.
• La vague 4 n'entre jamais dans le territoire de prix de la vague 1

Une directive commune appelée « alternance » observe que dans un motif de cinq vagues, les vagues 2 et 4 prennent souvent des formes alternées ; un mouvement simple et net dans la vague 2, par exemple, suggère un mouvement complexe et doux dans la vague 4. L'alternance peut se produire dans les vagues impulsives et correctives. Elliott a observé que les vagues alternées du même degré doivent être distinctives et uniques en termes de prix, de temps, de sévérité et de construction. Toutes les formations peuvent guider les influences sur l'action du marché. La période de temps couverte par chaque formation, cependant, est le principal facteur décisif dans la pleine manifestation de la règle de l'alternance. Une contre-tendance nette en vague 2 couvre une courte distance en unités horizontales. Cela devrait produire une correction contre-tendance latérale en vague 4, couvrant une distance plus longue en unités horizontales, et vice versa. L'alternance fournit aux analystes un avertissement de ce qu'il ne faut pas attendre lors de l'analyse des formations de vagues.

Les motifs de vagues correctives se déploient sous des formes connues sous le nom de zigzags, flats, ou triangles. À leur tour, ces motifs correctifs peuvent se combiner pour former des corrections plus complexes. De même, un motif correctif triangulaire est formé généralement en vague 4, mais très rarement en vague 2, et est l'indication de la fin d'une correction

Relations de Fibonacci

L'analyse par R. N. Elliott des propriétés mathématiques des vagues et des motifs l'amène à conclure que « la série de sommation de Fibonacci est la base du principe des vagues ». Les nombres de la suite de Fibonacci apparaissent de manière répétée dans les structures des vagues d'Elliott, y compris les vagues motrices (1, 3, 5), un cycle complet unique (8 vagues), et les motifs motrices complétés (89 vagues) et correctifs (55 vagues). Elliott a développé son modèle de marché avant de réaliser qu'il reflète la suite de Fibonacci : « Lorsque j'ai découvert l'action du principe des vagues des tendances du marché, je n'avais jamais entendu parler ni de la suite de Fibonacci, ni du diagramme de Pythagore ».

La suite de Fibonacci est également étroitement liée au nombre d'or (1,618). Les praticiens utilisent couramment ce ratio et les ratios associés pour établir des niveaux de support et de résistance pour les vagues du marché, à savoir les points de prix qui aident à définir les paramètres d'une tendance.

Le professeur de finance Roy Batchelor (en) et le chercheur Richard Ramyar, ancien directeur de la United Kingdom Society of Technical Analysts et ancien Global Head of Research chez Lipper et Thomson Reuters Wealth Management, ont étudié si les ratios de Fibonacci apparaissent de manière non aléatoire sur le marché boursier, comme le prévoit le modèle d'Elliott. Les chercheurs ont déclaré que « l'idée que les prix retracent à un ratio de Fibonacci ou à une fraction arrondie de la tendance précédente manque clairement de toute justification scientifique ». Ils ont également dit « il n'y a pas de différence significative entre les fréquences avec lesquelles les ratios de prix et de temps se produisent dans les cycles du Dow Jones Industrial Average, et les fréquences que nous pourrions nous attendre à voir apparaître au hasard dans une telle série temporelle ».

Après Elliott

Après la mort d'Elliott en 1948, d'autres techniciens de marché et professionnels financiers continuent d'utiliser le principe des vagues et de fournir des prévisions aux investisseurs. Charles Collins, qui a publié The Wave Principle d'Elliott et a aidé à introduire la théorie d'Elliott à Wall Street, déclare que les contributions d'Elliott à l'analyse technique sont aussi significatives que celles de Charles Dow. Hamilton Bolton, fondateur de Bank Credit Analyst, prône l'analyse des vagues auprès d'un large lectorat dans les années 1950 et 1960 dans ses commentaires annuels sur le marché et ses prévisions. Il introduit le principe des vagues à A. J. Frost (1908-1999), qui fournit des commentaires financiers hebdomadaires sur le Financial News Network dans les années 1980. Au cours de sa vie, les contributions de Frost au domaine sont de grande importance et aujourd'hui, la Canadian Society of Technical Analysts décerne chaque année le A. J. Frost Memorial Award à quelqu'un qui a également apporté une contribution significative au domaine de l'analyse technique.

Des découvertes supplémentaires de nouvelles règles et de nouveaux motifs de vagues sont découvertes après que Ralph Nelson Elliott a publié son œuvre originale. Glenn Neely, qui publie Elliott Waves in Motion en 1988 et Mastering Elliott Wave en 1990, utilise la théorie des vagues d'Elliott pour présenter la première approche scientifique et objective de la prévision du marché. Vers 1980, Neely consacre sa carrière à la recherche sur les vagues d'Elliott et quelques années plus tard, applique ce qu'il a appris en enseignant l'application du principe des vagues d'Elliott dans l'analyse du marché en temps réel. Au fil du temps, la méthode d'enseignement de Neely évolue pour inclure sa propre théorie des vagues appelée néo-vagues (qui est une extension de la théorie des vagues d'Elliott). La théorie néo-vagues et les règles supplémentaires aident à corriger les contradictions créées dans la théorie des vagues d'Elliott, qui se compose de différentes règles définissant des motifs d'impulsion simples des vagues du marché boursier. Selon la théorie néo-vagues, les principaux nouveaux motifs de vagues découverts sont : triangle neutre, formation diamétrale, formation symétrique, triangle d'extraction, terminal de 3e extension avec échec de la 5e, et alternance inverse.

Adoption et utilisation

Robert Prechter découvre le travail d'Elliott alors qu'il est employé comme technicien de marché chez Merrill Lynch dans les années 1970. Son bulletin d'information sur le marché auto-édité met en vedette son analyse des vagues d'Elliott pendant le marché haussier des années 1980 et donne à ses vues une exposition parmi les adeptes de l'analyse technique.

Critique

Benoît Mandelbrot, qui a développé des modèles mathématiques de la tarification du marché basés sur la géométrie fractale, exprime des réserves sur la validité des modèles de vagues : « Mais la prévision des vagues est une affaire très incertaine. C'est un art auquel le jugement subjectif des chartistes importe plus que le verdict objectif et reproductible des chiffres. Le bilan de ceci, comme de la plupart des analyses techniques, est au mieux mitigé. »

Robert Prechter a précédemment déclaré que les idées d'un article de Mandelbrot « proviennent de Ralph Nelson Elliott, qui les a présentées de manière plus complète et plus précise par rapport aux marchés du monde réel dans son livre de 1938 The Wave Principle ».

Les critiques avertissent que le principe des vagues est trop flou pour être utile, car les praticiens ne peuvent pas identifier de manière cohérente le début ou la fin des vagues, ce qui entraîne des prévisions sujettes à des révisions subjectives. L'analyste technique David Aronson écrit : « Le principe des vagues d'Elliott, tel qu'il est couramment pratiqué, n'est pas une théorie légitime, mais une histoire, et une histoire convaincante qui est éloquemment racontée par Robert Prechter. Le récit est particulièrement persuasif parce que la théorie a la capacité apparemment remarquable de s'adapter à tout segment de l'histoire du marché jusqu'à ses fluctuations les plus minimes. Je soutiens que cela est rendu possible par les règles mal définies de la méthode et la capacité de postuler un grand nombre de vagues imbriquées de magnitude variable. Cela donne à l'analyste d'Elliott la même liberté et flexibilité qui a permis aux astronomes pré-copernicien d'expliquer tous les mouvements planétaires observés même si leur théorie sous-jacente d'un univers centré sur la Terre était fausse. »

Certains analystes considèrent le principe des vagues d'Elliott comme trop dépassé pour être applicable aux marchés d'aujourd'hui, comme l'explique l'analyste de marché financier Glenn Neely, auteur de Mastering Elliott Wave : « Les vagues d'Elliott étaient une découverte incroyable pour son époque. Mais, à mesure que les technologies, les gouvernements, les économies et les systèmes sociaux ont changé, le comportement des gens a également changé. Ces changements ont affecté les motifs de vagues que R. N. Elliott a découverts. Par conséquent, l'application stricte des concepts orthodoxes des vagues d'Elliott aux marchés actuels fausse la précision des prévisions. Les marchés ont évolué, mais Elliott n'a pas évolué. »