Géocentrisme
Le géocentrisme est un modèle physique ancien, selon lequel la Terre se trouve immobile, au centre de l'Univers. Cette théorie date de l'Antiquité et a été notamment défendue par Aristote et Ptolémée. Elle a duré jusqu’à la fin du XVIIe siècle à la Renaissance pour être progressivement remplacée par l'héliocentrisme, selon lequel la Terre tourne autour du Soleil.
| Géocentrisme | ||
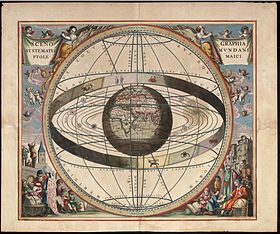 Reproduction du système géocentrique de Ptolémée (XVIIe siècle) | ||
| Définition | Le géocentrisme est une théorie de l'ordonnancement de l'Univers selon laquelle la terre est au centre du système spatial. | |
|---|---|---|
| Date d'apparition | Antiquité et Moyen Âge | |
| Partisans | Aristote, Ptolémée | |
| modifier |
||

Le géocentrisme est autant une tentative scientifique d'expliquer l'Univers qu'une conception philosophique de ce monde. Un principe régit toutes les théories géocentriques, un deuxième la plupart :
- la Terre est le centre de l'Univers, immobile de lieu (par an) et de position (par jour) : les changements des saisons et de jour et nuit se font donc par mouvements extérieurs à la Terre ;
- les mouvements des planètes (au sens ancien, le mot planète inclut le Soleil et la Lune, mais pas la Terre) doivent être parfaits, donc seul le cercle est autorisé, les mouvements angulaires ou rectilinéaires étant considérés comme brusquement abrupts, forcés.
Cosmologie des premiers Grecs
modifierDans la cosmologie des premiers philosophes grecs (vers 600 av. J.-C., Anaximandre, Anaximène, Thalès), la Terre est plate, les astres sont des corps fixés sur des sphères en révolution, le tout forme le cosmos.
Les philosophes pythagoriciens (fin du VIe siècle av. J.-C.) imaginent une Terre sphérique et dix sphères concentriques portant les différents astres. La dixième sphère est celle qui porte les étoiles. L'aspect le plus original du modèle des pythagoriciens est leur tentative de faire coïncider intervalles musicaux et distances entre les sphères. C'est ce qu'on appelle l'harmonie des sphères. Chaque sphère est censée produire un son dans son mouvement, son que l'on ne distingue pas car il fait partie du bruit de fond que l'on entend depuis notre naissance.
Le philosophe Platon voit la Terre comme une sphère au centre de l'Univers, entourée d'une sphère d'eau (épaisseur de deux rayons terrestres), d'une sphère d'air (épaisseur cinq rayons terrestres), et d'une sphère de feu (épaisseur de dix rayons terrestres). Les étoiles se trouvent dans la partie supérieure de la sphère de feu (soit à dix-huit rayons terrestres) alors que les sept planètes évoluent dans une région intermédiaire. Toutes ces sphères tournent de manière uniforme autour d'un même axe.
Eudoxe de Cnide imagine 27 sphères concentriques mais ne tournant pas suivant le même axe, ce qui permet d'expliquer les différences de latitude des planètes.
Héraclide du Pont (v. 388 - v. 310 av. J.-C.) propose un modèle mixte, de type géo-héliocentrique: Vénus et Mercure tournent autour du Soleil, tandis que la Terre reste stationnaire, les révolutions autour de son axe expliquant le mouvement apparent des corps célestes[1]. Cette théorie sera assez populaire dans l'Antiquité pour encore être reprise dans l'ouvrage encyclopédique de Martianus Capella vers 420, grâce à quoi elle sera connue de Copernic.
Le géocentrisme d'Aristote
modifierDans le modèle géocentrique la Terre est ronde. L'univers, alors fini dans l'espace, se divise en deux parties : le monde sublunaire et supralunaire. Le premier concernant tout ce qui est situé sous l'orbite de la Lune (la Terre et son atmosphère), est symbole de mouvement, d'incertitude, continuellement altéré et instable. Il semble ne répondre à aucune loi et est plutôt hasardeux. Les êtres vivants naissent, changent, et meurent. Le second, quant à lui, est immuable, parfait, stable et éternel. Rien ne peut s'y créer ni disparaître. Les astres étaient portés par 55 sphères concentriques et se déplaçaient à différentes vitesses, suivant une trajectoire circulaire, car le cercle (et par la même occasion, la sphère) était, d'après les pythagoriciens, la figure parfaite. La dernière sphère était celle des astres fixes (les étoiles) ; la première celle de la Lune. Pour Aristote, les sphères sont en cristal contrairement à celles d'Eudoxe (408-355 av. J.-C.) qui étaient constituées d'une matière appelée éther.
Cependant, un problème se posait quant à la trajectoire des planètes. Celles-ci présentaient par moments une rétrogradation, par laquelle elles semblaient revenir en arrière quelque temps avant de reprendre leur course dans le sens « normal ». Pour y répondre, tout en respectant le caractère parfait du cercle, Aristote imagina tout un système de sphères dont certaines ne sont là que pour faire tourner d'autres sphères qui, elles, porteront peut-être un astre. Voilà pourquoi il faut 55 sphères pour seulement six planètes.
La théorie des épicycles
modifierCette nouvelle théorie, généralement attribuée à Hipparque, mais fondée sur les travaux d'Apollonius de Perga (on ignore la part exacte de l'un et de l'autre) apparaît au IIe siècle av. J.-C. Les planètes tournent sur des roues appelées épicycles. Ceux-ci tournent eux-mêmes sur une autre roue — appelée déférent — dont le centre est la Terre. La rotation simultanée des deux permettait d'obtenir un mouvement complexe, éventuellement rétrograde, et d'expliquer celui des planètes et de la Lune, en préservant en grande partie les présupposés philosophiques de l'époque : les mouvements des astres sont circulaires, centrés sur la Terre et de vitesse uniforme.
L'élaboration de ce système constitue un progrès capital dans l'astronomie antique. En décomposant les mouvements complexes des astres en cercles parcourus par ceux-ci à vitesse constante, on rendait possible la confection de tables astronomiques très précises et très fiables. Ces tables permettront, par exemple, les premiers calculs d'éclipse solaire. Dès lors, la théorie géocentrique, fût-elle fausse, fonctionnait.
Les causes attribuées aux rotations diverses observées ou déduites
modifierSelon la lecture de Gilbert Walusinski ou Jean-René Roy (cf. Bibliographie) il semble qu'Aristote considère le nombre des sphères solides et leur interaction avec le mouvement du primum mobile (mouvement premier) comme une explication suffisante. Selon la lecture de Thomas d'Aquin dans la Somme Théologique, il faut l'action des esprits pour que la Lune poursuive son trajet mensuel et le Soleil son trajet annuel au sens inverse du mouvement du ciel. Or, Saint Thomas a commenté les livres 1 - 8 de la Physique d'Aristote, et il est mort avant d'avoir commenté jusqu'au bout Du ciel (De caelo et mundo), qu'il a tout de même commenté jusqu’à la fin du troisième livre. À la différence de Walusinski ou Roy, il considérait Aristote comme une autorité non pleinement dépassée dans la physique.
Le système de Ptolémée
modifierPtolémée, au IIe siècle, marque le sommet de l'évolution de la science astronomique de l'Antiquité. Après lui, il y aura encore des « commentateurs », parfois intéressants, comme Théon d'Alexandrie, mais aucune théorie nouvelle ne le remettra en question avant la Renaissance. Ptolémée perfectionne la théorie des épicycles, effectue un travail d'observations, de calculs et de compilation de résultats antérieurs, laissant une œuvre en treize volumes sur l'astronomie appelée la Grande Syntaxe. Traduite en arabe et diffusée sous le nom d’Almageste, cette œuvre aura une influence considérable sur l'astronomie des siècles suivants. Elle décrit notamment en détail les mouvements des planètes dans le modèle géocentrique.
Concernant le mouvement du Soleil, Ptolémée reprend le modèle d'Hipparque et l'explique selon deux modèles équivalents : un mouvement uniforme sur un cercle de rayon R dont le centre n'est pas la Terre (modèle excentrique) ou bien rotation du Soleil sur un épicycle dont le centre est situé sur un déférent de rayon R et centré sur la Terre, les deux rotations s'effectuant en sens contraire[2].
Concernant les planètes et afin de mieux rendre compte des observations, Ptolémée va modifier légèrement le modèle antérieur en introduisant la notion de point équant. L'équant est un point excentré duquel on voit la planète décrire une trajectoire avec une vitesse angulaire constante. Sous Aristote, ce point était confondu avec la Terre. Il introduit également l'excentrique, un épicycle inversé sur lequel tourne le centre du déférent. La Terre se trouve, elle, au symétrique de l'équant par rapport au centre de l'excentrique. Ce modèle, qui permet de mieux considérer les variations de vitesses des planètes, ne place donc plus la Terre en son centre mais un point « imaginaire » ne correspondant à l'emplacement d'aucun objet céleste. Grâce à cette nouvelle conception, Ptolémée obtient un accord bien meilleur avec les mesures les plus précises.
Ptolémée se borne à donner une exposition et des calculs géométriques des positions et mouvements observés et déduits, sans donner d'explication physique aux mouvements. Il précise toutefois que « les astres nagent dans un fluide parfait qui n’oppose aucune résistance à leurs mouvements[3] ». Il ne reprend donc pas à son compte les sphères de cristal d'Aristote, contrairement à une idée reçue.
Le système de Nasir ad-Din at-Tusi et d'Ibn Al-Shatir
modifierLes historiens et épistémologistes reconnaissent aujourd'hui l'apport des astronomes musulmans du Moyen Âge et plus particulièrement du perse Nasir ad-Din at-Tusi (1201-1274) et d'Ibn al-Shâtir (1304-1375) dans la remise en cause officielle des modèles du système planétaire de Ptolémée[4],[5],[6].
Les deux hommes faisaient partie de l'école de Maragha. Nasir al-Din al-Tusi a fait construire un observatoire et a étudié les mouvements de la Lune et du Soleil. À l'époque, les astronomes de Maragha se convainquirent que le précepte aristotélicien, selon lequel les mouvements dans l'univers ne peuvent être que circulaires ou rectilignes[réf. nécessaire], est faux. Nasir al-Din al-Tusi montrera de manière géométrique qu’on pouvait engendrer un mouvement rectiligne uniquement à partir de mouvements circulaires grâce à l’hypocycloïde[7].
Dans son ouvrage intitulé al-Tadhkira fi 'ilm al-hay'a (Mémorandum des sciences de l'Astronomie)[8], Nasir ad-Din at-Tusi se demande d'abord si la Terre n’était pas elle-même en mouvement et comment rendre cette hypothèse compatible avec les nouveaux calculs astronomiques effectués à l'observatoire de Maragha[9]. Sa proposition est d'éliminer définitivement le concept de l'équant dans le modèle de Ptolémée, jugé incompatible avec les données d'observations des mouvements des corps célestes, et simplifie ainsi considérablement le modèle planétaire grec en proposant un nouveau système (selon les historiens jugé 'ingénieux pour l'époque') de mouvements circulaires uniformes pour rendre compte des variations de distance de la Lune à la Terre. Ce système est connu sous le nom du « couple d'Al-Tusi »[10],[11], ou « hypocycloïde d'Al Tusi » ; On retrouve d'ailleurs ce système à l'identique dans l'œuvre de Nicolas Copernic intitulée De revolutionibus orbium coelestium sans que l'on sache comment celui-ci se le serait procuré[11].
Quant à Ibn al-Shatir (Damas vers 1350), il avait continué le travail d'Al Tusi en proposant un autre système planétaire celui-ci totalement concentrique, mécaniquement acceptable, et généralisant les idées d’al-Tusi. Selon les historiens[Lesquels ?], Nicolas Copernic aurait également repris le modèle Terre-Lune-Soleil d’Ibn al-Shatir pour émettre sa théorie de l'héliocentrisme.[réf. nécessaire]
On cite deux autres astronomes musulmans dans cette aventure des modèles célestes. Il s'agit d'Al-Battani, surnommé « l’imitateur parfait de Ptolémée »[12] (mort en 929) et Al-Zarqali qui, pendant quarante années pour le premier et vingt années pour le second, ont mesuré l'un en Orient, l'autre en Espagne musulmane, jour après jour les positions exactes du Soleil par rapport à la Terre et ont dressé des tables de la précession des équinoxes ; mais, ce phénomène, connu depuis la plus haute antiquité, découvert, compris et chiffré par Hipparque, avait déjà bénéficié de mesures s’étendant sur plus de mille ans. Or, les astronomes arabes n’apportèrent, en ce qui concerne la théorie, aucun perfectionnement aux hypothèses de base, se bornant à résumer l’Almageste et même, les continuateurs médiocres de Ptolémée[13]. Du fait du désaccord des observateurs et des valeurs différentes qu’ils trouvaient pour le calcul de la précession, les astronomes arabes imaginèrent le système de la « trépidation des équinoxes », rejeté depuis l'Antiquité et dérivé des Commentaires sur les tables nouvelles de Ptolémée de Théon d'Alexandrie. D’où le jugement sévère de Pierre Duhem : « La science islamique est faite en grande partie du butin razzié sur la science hellénique de la décadence[14]. » Les tables d'Al-Battani sont citées dans les dernières pages de l'ouvrage De revolutionibus orbium coelestium de Copernic[réf. nécessaire]. Al-Zarqali aurait établi pour sa part des tables précises (mais rien ne prouve qu’il en soit l’auteur[15]) sur le mouvement des planètes, connues sous le nom de Tables de Tolède , basées sur les observations qu'il a effectuées à Tolède entre 1061 et 1080[16]. Ces tables étaient d'une précision telle qu'elles lui permirent de prédire des éclipses[17].
Le système de Tycho Brahe
modifierAu XVIe siècle, l'astronome danois Tycho Brahe repense totalement la conception géocentrique de Ptolémée. Connaissant le modèle héliocentrique de Copernic, il ne pouvait l'accepter, pour des raisons religieuses plus que scientifiques. Ses observations le conduisent cependant à élaborer un modèle personnel hybride mélangeant géocentrisme (quant à l'Univers) et héliocentrisme (quant au Système Solaire, sauf la Terre) : la Lune et le Soleil tournent autour de la Terre — qui reste le centre de l'Univers — tandis que les planètes tournent autour du Soleil. Ce modèle a été créé afin de répondre au problème des phases de Vénus dans le système géocentrique précédent.
D'après Aristote, les comètes faisaient partie du monde sublunaire à cause de leurs trajectoires très excentriques et étaient même associées à des phénomènes météorologiques. Elles ne pouvaient faire partie du monde supralunaire où tout était ordonné car elles risquaient de heurter les sphères cristallines. Cependant, Tycho Brahe démontre que la comète de 1577 est à une distance supérieure à quatre fois la distance Terre-Lune et fait donc partie du monde supralunaire, infirmant la théorie des sphères matérielles. Les sphères n'étaient donc qu'une vue de l'esprit.
Cette immuabilité du monde supralunaire avait été remise en cause par l'observation d'une nova cinq ans auparavant. Celle-ci apparut puis disparut 18 jours plus tard, là où les objets étaient censés ne jamais mourir.
La fin du géocentrisme
modifierLes débats historiques autour du géocentrisme
modifierDans le courant scolastique, Nicole Oresme spécule sur la possibilité de l'héliocentrisme, de sa compatibilité avec les observations quotidiennes et astronomiques. Il conclut que l'héliocentrisme n'était pas réfutable par les observations, mais de fait faux. Nicolas Copernic reprend ses arguments, mais ajoute qu'il peut mieux calculer les mouvements planétaires en avance en partant du modèle héliocentrique. Tycho Brahe, lui géocentrique, identifiant l'excentrique du Ptolémée avec le Soleil, affine encore les calculs, au-delà de Copernic et au-delà de Ptolémée. Son assistant Johannes Kepler retourne à l'hypothèse héliocentrique, cette fois en employant des orbites elliptiques et une relation (loi de Titius-Bode) sur les distances des orbites (la loi de Titius-Bode — cette loi, en revanche, se révèlera parfaitement dissociable du reste de la théorie, et ne dispose à ce jour d'aucune justification théorique). Ce modèle va être accepté par Isaac Newton et devenir le modèle héliocentrique classique de celui-ci, justifié par sa nouvelle physique.
Théories de la Scolastique classique
modifier« Secunda ratio ad idem probandum talis est. In moventibus et motis ordinatis, quorum scilicet unum per ordinem ab alio movetur, hoc necesse est inveniri, quod, remoto primo movente vel cessante a motione, nullum aliorum movebit neque movebitur: quia primum est causa movendi omnibus aliis. Sed si sint moventia et mota per ordinem in infinitum, non erit aliquod primum movens, sed omnia erunt quasi media moventia. Ergo nullum aliorum poterit moveri. Et sic nihil movebitur in mundo. »[18] (« Un second raisonnement pour démontrer la même chose s'énonce ainsi : lorsque les moteurs et les mobiles sont ordonnés[19], c'est-à-dire dont chacun à tour de rôle est mû par un autre, il doit nécessairement se vérifier que le premier moteur étant supprimé ou cessant son mouvement, aucun des autres ne bougera ni ne sera mû : car le premier est cause du mouvement pour tous les autres. Mais s'il existe des moteurs et des mobiles, tour à tour, à l'infini, il n'y aura aucun premier moteur, mais tous seront pour ainsi dire des moteurs intermédiaires. Donc aucun d'entre eux ne pourra être mû. Et ainsi rien ne bougera dans le monde. »)
Dans ce texte, Thomas d'Aquin veut dire que par exemple les courants de l'Océan sont mus par les Vents de Passage, qui sont mus par la sphère de la Lune, et ainsi de suite jusqu'au primum motum (mouvement premier), le ciel, ou la sphère des étoiles fixes qui, lui, est mû par Dieu. Cette épreuve de Dieu, dit-il, est rapportée depuis le VIe livre des Physiques par Aristote :
« Aristote (...) affirmait que les corps célestes sont mus par des substances spirituelles ; et il a tenté de fixer leur nombre selon le nombre des mouvements qui se manifestent dans les astres. »
« Il ne pensait pas que des substances spirituelles exercent une influence immédiate sur des corps inférieurs, sauf peut-être les âmes humaines agissant sur leur corps. Et cela parce qu’il n’estimait pas qu’il puisse y avoir dans les corps inférieurs d’autres activités que leurs activités naturelles, pour lesquelles suffisait le mouvement transmis par les corps célestes. Mais nous croyons que beaucoup de choses s’accomplissent dans les corps inférieurs en dehors de leurs activités naturelles, qui ne peuvent s’expliquer suffisamment par l’action des corps célestes ; nous estimons donc nécessaire de tenir que les anges ont une influence immédiate non seulement sur les corps célestes, mais même sur les corps inférieurs. »[20]
Le rôle de Galilée
modifierUne nouvelle conception de la physique
modifierOn définit aujourd'hui une expérience physique ainsi :
Une expérience est un protocole matériel permettant de mesurer certains phénomènes dont la théorie donne une représentation conceptuelle. Il est illusoire d'isoler une expérience de la théorie associée. Le physicien ne mesure évidemment pas des choses au hasard ; il faut qu'il ait à l'esprit l'univers conceptuel d'une théorie. Aristote n'a jamais pensé à calculer le temps que met une pierre lâchée pour atteindre le sol, simplement parce que sa conception du monde sublunaire n'avait rien à faire avec une telle quantification. Cette expérience a dû attendre Galilée pour être réalisée.
Ces quantifications ont permis à la nouvelle physique de Galilée et de Newton d'atteindre une exactitude auparavant non conçue : mais elle comporte d'autres éléments que la seule quantification. Pour Aristote, le lourd et le léger étaient deux qualités opposées. Pour Galilée le lourd était une qualité essentielle de la matière et le léger devient par là un simple manque de matière, une négation. Newton accepte cette conception du lourd et du léger, et il y ajoute la théorie de gravitation ou attraction universelle qui, par là, est une théorie uniquement de l'attraction du lourd par le lourd. Ni l'un ni l'autre n'excluent l'action des esprits comme irréelle, mais tous les deux la trouvent négligeable quant à l'étude de la nature. Ni l'un ni l'autre ne l'acceptent donc comme cause strictement contemporaine d'aucun mouvement. Et là ils introduisent aussi le concept d'un mouvement prolongé tant qu'il n'est pas arrêté. Désormais, gravitation et inertie, comprenant la continuation du mouvement, deviennent les seules causes acceptées pour l'astronomie.
L'emploi de la parallaxe
modifierDans le procès de Galilée, l'Inquisiteur St Robert Bellarmin fit l'objection que, si la Terre se mouvait, on devrait observer une parallaxe par rapport aux étoiles. Mais aucune parallaxe n'ayant été mesurée, ce fait devenait un argument contre l'héliocentrisme. Galilée répondit que les étoiles étaient trop lointaines pour que la parallaxe puisse être vue et mesurée avec les instruments d'alors.
La parallaxe mesurée par Bessel correspond à celle prévisible en admettant la théorie héliocentrique. Bien entendu, la présentation de la parallaxe comme une preuve de l'héliocentrisme signifie qu'on suppose les mouvements des autres étoiles par rapport au Soleil comme négligeables devant les mouvements des objets du système solaire. C'est un exemple d'application du principe de parcimonie : on ne peut pas attribuer à l'ensemble des étoiles de l'univers un mouvement collectif (les étoiles les plus lointaines devant se déplacer plus vite…) pour expliquer les mêmes observations qu'on peut expliquer par le mouvement d'un seul objet, la Terre.
La nouvelle physique s'impose
modifierEn 1687, Isaac Newton publie le premier volume de son Philosophiae Naturalis Principia Mathematica. Il inclut les lois connues aujourd'hui comme les trois lois du mouvement de Newton, ainsi que la loi universelle de la gravitation et le principe de relativité.
Ces nouvelles lois prédisent le mouvement de tout corps en fonction des forces qui s'exercent sur lui. Elles sont utilisées dès lors et jusqu’à aujourd'hui pour tous les calculs en mécanique (à l'exception de quelques situations extrêmes réclamant la théorie de la relativité ou la physique quantique). Elles constituent la première mécanique cohérente, pouvant expliquer tous les phénomènes de la vie quotidienne.
En admettant que le Soleil est largement plus massif que les planètes, la loi de la gravitation et les lois du mouvement permettent de démontrer que les mouvements des planètes sont conformes aux lois de Kepler, que Kepler lui-même avait constaté expérimentalement. L'héliocentrisme est conforté, ainsi que le caractère elliptique des orbites.
Toutefois ce n'est qu'en 1727, à la suite de la publication des travaux de James Bradley sur l'aberration de la lumière, qu'est apportée la première preuve expérimentale du mouvement de la Terre autour du Soleil[21].
Capables de prévoir les trajectoires des comètes comme les dates des éclipses, les lois de Newton proposent un cadre physique à tous les mouvements cosmiques presque sans intervention d'autres forces. Presque car Newton lui-même affirmait que quand les planètes quittaient leurs orbites, Dieu les y replaçait. Pierre-Simon de Laplace démontra plus tard que les lois de Newton permettent au système solaire d'être suffisamment stable pour se maintenir sans intervention extérieure.
Importance philosophique
modifierL'idée que la Terre devait être au centre de l'Univers découlait en grande partie d'une vision du monde. Aristote, en effet, avait construit un système suivant des critères d'esthétique (exigence de sphères parfaites) et de l'importance qu'il attribuait aux objets. Il s'agit d'un modèle surtout intuitif, qui attribue des comportements différents aux objets terrestres et célestes (il faut attendre Newton pour donner une explication commune aux mouvements des astres et à la chute des corps).
Ce caractère intuitif est initialement la force du modèle géocentriste : l'homme ne ressent pas de mouvement de la Terre, et les objets célestes ne tombent pas comme les objets terrestres. Mais selon les critères, le rôle prépondérant de l'intuition fait juger ce modèle comme non scientifique.
L'exigence de perfection des sphères se retourna aussi contre le géocentrisme ; la découverte par Galilée des cratères lunaires le confortait dans la critique de ce modèle.
Position de l'Église
modifierLa conception du monde d'Aristote était largement reprise par l'Église catholique romaine, comme le montrait l'importance de la philosophie scolastique.
De plus, certains passages de l'Ancien Testament étaient interprétés comme impliquant le géocentrisme, selon les traductions (par exemple dans le Psaume 93 « Aussi le monde est ferme, il ne chancelle pas. », le mot « chanceler » pouvant être remplacé par « bouger »).
Cela n'exclut toutefois pas les recherches. Nicolas Copernic lui-même était un chanoine.
Face à Galilée
modifierLe pape Urbain VIII avait autorisé Galilée à publier son ouvrage, à condition qu'il place sur le même plan les théories de Copernic et de Ptolémée ; Galilée présenta les deux théories, mais en favorisant tout de même celle de Copernic.
Galilée fut accusé d'hérésie, et finalement, dut renier ses convictions pour éviter une condamnation à mort. Il fut condamné à la prison à vie, commuée en assignation à résidence par Urbain VIII.
Face aux passages de l'Ancien Testament, Galilée n'avait pas cherché à discuter leur interprétation, mais avait contesté que la lecture littérale de la Bible puisse servir de référence en science.
Ce procès est particulièrement important, car il marque ce que certains considèrent comme un conflit entre la science et la religion. Pour d'autres, il oppose plutôt ceux qui cherchent l'opposition entre religion et science (ceux qui ont condamné Galilée) à ceux qui cherchent à les concilier (comme Galilée lui-même). Dans tous les cas, le procès de Galilée devint le symbole de l'opposition entre les nouveaux scientifiques et les autorités religieuses. De plus, le refus de lire la Bible littéralement en matière de science devint plus tard essentiel dans l'opposition entre créationnisme et théorie de l'évolution.
Ce n'est que vers 1750, après la preuve expérimentale apportée par James Bradley, que l'Église, au cours du pontificat de Benoit XIV, abandonna le modèle géocentrique, et c'est bien plus tard encore qu'elle reconnut avoir fait erreur dans le procès de Galilée, et lui donna raison dans sa lecture de la Bible en matière de science[22] : le , le pape Jean-Paul II rendit hommage au savant lors de son discours aux participants à la session plénière de l'Académie pontificale des sciences[23]. Il y reconnaissait clairement les erreurs de certains théologiens du XVIIe siècle dans l'affaire : « Ainsi la science nouvelle, avec ses méthodes et la liberté de recherche qu'elle suppose, obligeait les théologiens à s'interroger sur leurs propres critères d'interprétation de l'Écriture. La plupart n'ont pas su le faire. » « Paradoxalement, Galilée, croyant sincère, s'est montré plus perspicace sur ce point que ses adversaires théologiens. « Si l'écriture ne peut errer, écrit-il à Benedetto Castelli, certains de ses interprètes et commentateurs le peuvent, et de plusieurs façons ». On connaît aussi sa lettre à Christine de Lorraine (1615) qui est comme un petit traité d'herméneutique biblique. »
Modèles et réalité
modifierSi l'on a une conception du monde telle qu'on exige que l'homme, donc la Terre, soit au centre de l'Univers, un recours possible est de considérer que le modèle actuel des astronomes, dans lequel la Terre est mobile (tournant autour du Soleil, lui-même en mouvement dans la Voie lactée, etc.) ne doit être considéré que comme un modèle commode pour leurs calculs.
Cette position est celle du Parti dans le roman 1984. Il s'agit d'un exemple de la « doublepensée », c'est-à-dire la pratique du Parti d'exiger de chacun qu'il accepte d'admettre des choses contradictoires sans utiliser son esprit critique pour relever ces contradictions.
Dans Adieu la raison, Paul Feyerabend défend que les modèles des physiciens ne doivent être considérés que comme utiles à la fin de faire des prédictions, et conteste l'idée de Galilée selon laquelle les modèles considérés comme vrais par les astronomes doivent être intégrés au savoir commun tels quels. Pour lui, l'Église avait raison de refuser de laisser à l'astronomie le statut de réalité. Un domaine plus large doit permettre de définir ce qu'on accepte comme réalité parmi les modèles des scientifiques, et Feyerabend estime que l'Église, en choisissant la foi comme étant ce domaine plus large, choisissait un cadre plus acceptable par rapport aux soucis humains.
Une telle position est toutefois exceptionnelle. Elle n'est pas très populaire chez les physiciens, qui considèrent plus souvent leurs modèles comme réels. Dans 1984, cette position n'était pas à prendre en exemple, puisqu'elle servait à illustrer l'hypocrisie. Les partisans de Galilée s'amusent du paradoxe que représentent les critiques modernes de Galilée comme Feyerabend, qui en viennent à défendre l'Église ancienne contre Galilée et l'Église moderne, alors que ces penseurs sont généralement de gauche politiquement[22]
Le géocentrisme contemporain
modifierStatut dans la science actuelle
modifierRéférentiels usuels
modifierLes référentiels permettant de mettre en évidence les approximations des points de vue géocentriques et héliocentriques sont les suivants :
- référentiel terrestre centré en un point de la Terre, ses axes sont liés à la rotation terrestre. Par exemple, le référentiel terrestre peut se définir sur un terrain de foot comme un référentiel centré au point de corner, donc les axes sont la ligne de touche, la ligne de but et le poteau de corner ;
- référentiel géocentrique : a pour origine le centre de gravité terrestre, et ses axes sont définis par rapport à des étoiles lointaines ;
- référentiel héliocentrique : a pour point fixe le centre du Soleil, et de même ses axes sont définis par rapport à des étoiles lointaines.
L'utilisation du référentiel géocentrique néglige donc le mouvement de la Terre autour du Soleil, et le référentiel terrestre néglige la rotation de la Terre sur elle-même. Ces référentiels peuvent être considérés comme étant en première approximation galiléens tant que la durée de l'expérience est courte en comparaison de la durée caractéristique de « non-galiléanité » du référentiel considéré : respectivement une journée pour le référentiel terrestre, un an pour le référentiel géocentrique et une dizaine d'années (~ période de révolution de Jupiter) pour le référentiel héliocentrique.
La rotation en mécanique
modifierPour comprendre les effets provoqués par le passage d'un référentiel à l'autre, il faut préciser quelques points de cinématique.
Un point A en rotation autour d'un point B à la vitesse angulaire ω sur une trajectoire de rayon R a une vitesse instantanée de valeur V=ωR. À tout instant, le point A possède une vitesse de valeur V de direction tangente au cercle, et une accélération de valeur a=ω²R dirigée vers le point B. On peut également exprimer cette accélération par a = V²/R.
Or, Galilée a mis en évidence que les vitesses ne sont pas ressenties pour elles-mêmes, seules les accélérations le sont, proportionnellement à leur valeur. Avec la relativité restreinte, Albert Einstein confirma que cette indifférence de la vitesse est vraie pour toutes les lois de la physique, électromagnétisme (donc lumière) compris.
En pratique, cela signifie que la rotation de la Terre décrite par Galilée produit très peu de mouvement sensible. Mais la rotation de la Terre autour du Soleil est bien moins sensible encore. Et c'est encore pour cela que le mouvement de la Terre par rapport au centre galactique, de 200km/s, est bien plus difficile à mettre en évidence que celui par rapport au Soleil (ce qui revient à dire qu'on peut généralement le négliger), d'une vitesse de 30km/s.
Cinématique et dynamique
modifierLa cinématique consiste à établir des équations donnant les positions d'objets au cours du temps, sans faire intervenir de notions de forces. Du point de vue de la cinématique, il est parfaitement possible de choisir le centre de la Terre comme point origine du repère, sans que cela engendre d'erreur.
On peut faire ce choix quand on se pose un problème ne concernant que les satellites de la Terre, et donc en ne s'intéressant qu'aux mouvements de ces satellites par rapport à elle. Typiquement, pour une constellation de satellites de télévision, on utilise les trajectoires des satellites dans un repère géocentrique pour démontrer qu'il y a toujours un satellite en vue d'une zone précise.
En effet, les observations de Galilée étaient compatibles avec le modèle de Copernic, non avec celui de Ptolémée. On peut en revanche construire un système compatible avec toutes les observations astronomiques, en mettant le Soleil en rotation autour de la Terre, et les autres objets en rotation autour du Soleil comme dans le modèle de Copernic. Mais une fois toutes les planètes considérées, le modèle obtenu apparaît comme inutilement compliqué en comparaison de celui de Copernic.
En dynamique, le choix du référentiel n'est plus aussi libre. La dynamique exige d'expliquer les mouvements par des forces, donc le choix d'un mauvais référentiel impose d'ajouter des forces fictives pour faire correspondre les trajectoires aux forces en présence. D'un point de vue physique, le référentiel terrestre est acceptable pour la plupart des expériences de la vie quotidienne. En revanche, dès qu'on fait des mesures précises, le référentiel terrestre nécessite qu'on lui adjoigne des forces fictives traduisant son caractère non-galiléen.
L'Univers n'a pas de centre
modifierNewton calcula que dans un univers limité, quelle que soit la répartition initiale des étoiles, toute la matière finissait par se regrouper sous l'effet de la gravité. Il postula donc que l'Univers était infini, rempli d'un nombre infini d'étoiles. Aujourd'hui, les cosmologues ont établi que l'Univers est ou bien infini, ou bien refermé sur lui-même[Passage contradictoire] (l'équivalent tridimensionnel de la surface d'une sphère). Prétendre que la Terre, ou même le Soleil, serait au centre de l'Univers, perd tout son sens dans les deux cas (de même qu'aucun point à la surface de la Terre ne peut en être le centre)[réf. nécessaire].
Une autre question est de savoir si la Terre se situe à un lieu particulier de l'Univers, qui en ferait un point d'observation privilégié. Même sur un domaine tout à fait physique, cette question n'est pas encore tranchée, mais les astrophysiciens estiment plus prudent d'admettre que ce n'est pas le cas et de chercher à expliquer la géométrie de l'Univers en considérant qu'elle doit être la même depuis tout point d'observation. La révolution copernicienne ayant retiré à la Terre son statut de centre de l'Univers, cette supposition a été appelée principe de Copernic.
Question de l'immobilité
modifierLa relativité galiléenne rend caduque l'idée qu'un référentiel serait le référentiel absolu, par rapport auquel on peut définir les mouvements de tous les objets de l'univers. Newton lui-même supposait l'existence d'un tel référentiel, mais montrait que les lois de la physique s'appliquaient de même dans tout référentiel en translation par rapport à celui-ci, qui devint de fait inutile. (Augustin Fresnel introduisit un milieu inamovible, l'éther, pour la propagation de la lumière, mais la théorie de la relativité supprima cet artefact). Un référentiel ne peut donc pas être absolu.
L'enjeu devient alors de savoir si la Terre ou le Soleil constituent des référentiels inertiels, ou référentiels galiléens, c'est-à-dire si en considérant l'un des deux comme fixe, on obtient des mouvements pour tous les astres compatibles avec les forces qu'ils subissent. Cette propriété est définie à une translation rectiligne près, ce qui signifie que si on trouve un référentiel vérifiant cette propriété, un autre référentiel dont le centre se déplace à vitesse constante en valeur comme en direction vérifie également cette propriété. En revanche cette propriété ne peut être vérifiée simultanément par des référentiels n'étant pas en translation. Ce qui signifie que les référentiels centrés sur la Terre et le Soleil ne peuvent être tous deux inertiels ou même quasi-inertiels (ou du moins que l'un d'eux aura des imperfections largement supérieures).
La relativité générale rend purement locale la notion de référentiel. Le problème de l'immobilité de la Terre n'est pas aboli pour autant : même avec la relativité générale, si on construit un système de coordonnées dans lequel la Terre est fixe, les objets qui ne sont soumis à aucune force non gravitationnelle ne suivent pas des géodésiques (la relativité générale incluant la gravité dans la courbure de l'univers). Au contraire, la trajectoire de la Terre dans un système de coordonnées où le Soleil est fixe est très proche d'une géodésique. Si les opérateurs sont plus compliqués, il ne faut pas pour autant croire que la relativité mettrait sur un pied d'égalité le géocentrisme et l'héliocentrisme, ou tout système encore plus précis.
Accroissement de la précision
modifierLa recherche d'un référentiel inertiel a permis de conclure que le référentiel héliocentrique est une très bonne approximation d'un référentiel galiléen, mais que le référentiel choisissant comme point fixe le centre de masse du système solaire (légèrement différent du centre du Soleil), ou référentiel de Copernic était encore meilleur. Mais le référentiel géocentrique reste suffisant pour une étude en première approximation du mouvement d'un satellite terrestre, et le référentiel terrestre suffit pour la plupart des expériences courantes.
La vitesse de la Terre dans le référentiel géocentrique est d'environ un dixième de la vitesse du Soleil dans le système de coordonnées galactiques. Cependant la relativité montre que les vitesses rectilignes ne produisent pas de mouvement détectable. Or le mouvement du Soleil est quasiment circulaire, mais avec un rayon si grand qu'il apparaît comme rectiligne (avec une accélération extrêmement faible en direction de ce centre). C'est pourquoi l'imperfection du référentiel héliocentrique est extrêmement faible par rapport à celle du référentiel géocentrique. À noter que le caractère indécelable du mouvement rectiligne uniforme et la faiblesse de cette accélération expliquent que le mouvement du système solaire tout entier dans les coordonnées galactiques soit resté inconnu plus longtemps que le mouvement de la Terre autour du Soleil.
Dans les expériences et problèmes courants
modifierCertains défenseurs du géocentrisme soulignent que selon les problèmes considérés, les physiciens peuvent considérer la Terre comme immobile. En fait, cela ne signifie pas que les physiciens reviennent au géocentrisme, mais simplement qu'ils admettent que pour le problème considéré, la différence obtenue sera négligeable.
Typiquement, la déviation vers l'est peut être calculée avec une précision suffisante même en admettant que la Terre tourne sur elle-même mais que son centre est immobile. Pour des problèmes impliquant des distances encore plus faibles, on peut non seulement admettre que la Terre est immobile, mais aussi qu'elle est plate, et le champ de pesanteur indépendant de l'altitude.
L'utilisation du référentiel géocentrique n'implique donc pas l'acceptation du géocentrisme.
Il faut noter que dans la plupart des expériences courantes, on suppose que la gravité ne dépend pas de l'altitude (absurde au vu de son expression rigoureuse, évident en évaluant numériquement les premiers termes du développement limité). En fait, la plupart des calculs de trajectoire d'un objet à la surface de la Terre peuvent même se faire en supposant que la Terre est plate.
Statut final
modifierEn conséquence de toutes les considérations décrites ci-dessus, on doit conclure qu'il est impossible d'affirmer l'immobilité ou le caractère central d'un objet céleste quel qu'il soit.
De plus, le fait qu'il existe de nombreuses corrections à faire par rapport à l'héliocentrisme ne retire pas sa vérité à la phrase « la Terre tourne autour du Soleil », car par rapport à l'hypothèse de l'immobilité de la Terre, la rotation de la Terre sur elle-même élimine les accélérations parasites les plus importantes, et par rapport à l'hypothèse de fixité d'une Terre tournant sur elle-même, la Terre tournant autour du Soleil diminue encore fortement les résidus.
Actualité du géocentrisme
modifierPhénoménologie
modifierDans son étude L’Arche-originaire Terre ne se meut pas : Recherches fondamentales sur l’origine phénoménologique de la spatialité de la nature (1934), le phénoménologue Edmund Husserl cherche à démontrer que le point de vue de la physique objective ne saurait se substituer au point de vue existentiel et perceptif de l'humain. Husserl repense la notion d'espace sur la base d'une étude immédiate, et non médiate comme s'y attachent les sciences modernes, de la nature. L'espace n'est pas seulement une donnée objective de l'expérience : c'est un cadre dans lequel tous les êtres fondent leur existence. De cette façon, selon Husserl, la terre ne se meut pas : elle n'est pas qu'un corps céleste parmi d'autres, pour l'homme, elle est aussi le sol fondateur et irremplaçable de sa perception et de son jugement. En ce sens, elle est « centrale », et le firmament tourne autour d'elle en tant qu'elle est non pas seulement vue, mais vécue, comme l'« archê » de notre perception.
La phénoménologie géocentrique d'Husserl a beaucoup intéressé jusqu'à aujourd'hui les chercheurs du fait de sa philosophie de la nature audacieuse[réf. nécessaire].
Défenseurs du géocentrisme
modifierBien que l'héliocentrisme soit une vérité de la physique reconnue par l'ensemble de la communauté scientifique, depuis la reconnaissance progressive du travail de Galilée, il reste que le modèle géocentrique est toujours sérieusement défendu, non plus du point de vue de la physique, mais du point de vue sémantique et « métaphysique »[réf. nécessaire].
Dans une perspective « métaphysique », Julius Evola explique :
« La théorie géocentrique saisissait dans le monde des apparences sensibles un aspect propre à servir de support à une vérité d'une autre sorte et inattaquable: la vérité concernant l' "être", la centralité spirituelle, comme principe de l'essence véritable de l'homme. » – L'arc et la massue, chapitre 1: "Civilisations du temps et civilisations de l'espace", trad. Philippe Baillet.
Plus généralement, le géocentrisme en particulier ne propose pas une théorie concurrente ou opposée à l'héliocentrisme en physique : à la façon d'Andreas Osiander dans sa préface à la Révolution des orbes célestes de Copernic (1543), ils défendent contre la concurrence des hypothèses la théorie de l'équivalence des hypothèses. Cette théorie propose différents points de vue de la connaissance. Pour le philosophe Jean Borella, dans La Crise du symbolisme religieux et Histoire et théorie du symbole, la cosmologie ancienne et les sciences traditionnelles se rapprochant de la métaphysique étudient la nature sémantique. La nature est observée comme délivreuse de sens pour l'existence, étant entendu que toute connaissance est une herméneutique du réel. Cette approche est strictement qualitative, elle s'appuie sur la faculté cognitive de l'intuition et prend acte du fait que toute information tirée de l'expérience est un contenu objectif de sens. La physique moderne, quant à elle, prend pour objet la nature comprise comme nature physique, mesurable et quantifiable avec les instruments et suivant les règles méthodologiques de l'analyse empirique. Ainsi, le point de vue géocentrique ici mobilisé est soit phénoménologique, soit astrologique[24]: son paradigme est sémantique, voire métaphysique, et non physique.
Il existe donc une défense sérieuse du géocentrisme compris comme théorie sémantique et symbolique et non comme théorie physique.
En physique
modifierCertains courants, souvent d'inspiration chrétienne ou musulmane, persistent en revanche à défendre le modèle géocentrique d'un point de vue physique et astronomique[réf. nécessaire]. Les arguments présentés se basent parfois sur des résultats de la physique du XXe siècle : attribution du résultat nul de l'expérience de Michelson-Morley à l'immobilité de la Terre[25], prétention que la relativité met tous les référentiels sur le même plan[26]. Les argumentations sont souvent basées sur une mauvaise compréhension de la physique : Conservapedia par exemple affirme qu'aujourd'hui les physiciens emploient aussi bien la théorie héliocentrique que la théorie géocentrique, confondant modèle et théorie (faire les calculs dans le référentiel géocentrique ne signifie pas qu'on croit que la Terre est immobile, mais que l'on sait que le résultat du calcul correspondra à la réalité même en faisant cette hypothèse). The Final Theory, livre de Mark McCutcheon défendant le géocentrisme, prétend que la physique actuelle est incapable d'expliquer comment la lumière accélère en passant du verre à l'air (confondant vitesse et quantité de mouvement)[27].
Les errements initiaux de Foucault lors de la mise au point de son pendule sont également évoqués[28].
Bibliographie
modifier- Ciel, passé, présent, de Gilbert Walusinski
- L'Astronomie et son histoire, de Jean-René Roy
- L'Image du Monde des Babyloniens à Newton, de Arkan Simaan et Joëlle Fontaine, Adapt Éditions, 1999.
- Le Monde des sphères, 2 volumes, Les Belles Lettres, Michel-Pierre Lerner.
- Les Somnambules, Éditions Calmann-Lévy, Paris 1960, Arthur Koestler.
Notes et références
modifier- (en) William Harris Stahl, Martianus Capella and the Seven Liberal Arts : volume I. The quadrivium of Martianus Capella. Latin traditions in the mathematical sciences, New York, Columbia University Press, , p. 175
- George Saliba, « Les théories planétaires », dans Roshdi Rashed, Histoire des sciences arabes : Astronomie Théorique et appliquée, t. 1, Seuil, (ISBN 978-2-02-062025-3), p. 74/75
- N. Halma, L’Almageste de Ptolémée, XIII, 12, édition et traduction, Paris, 2 vol., 1813-1817, réimprimée par Hermann, Paris - 1927. - Halma, op. cit., préface, p. 15-16.
- Cf. le § « Critique du ptolémaïsme et nouvelles écoles (1025-1450) » dans « Astronomie arabe ».
- (en) A. I. Sabra, « Configuring the Universe: Aporetic, Problem Solving, and Kinematic Modeling as Themes of Arabic Astronomy », Perspectives on Science, vol. 6, 1998, p. 288-330.
- Ahmed Djebbar, Une histoire de la science arabe [détail de l’édition], p. 192-197.
- (en) George Saliba, A History of Arabic Astronomy: Planetary Theories During the Golden Age of Islam, New York University Press, 1994b (ISBN 0814780237), p. 152 et suivantes sur Google Livres.
- Nasir Al-Din Al-Tusi, traduit par J. Ragep, Springer-Verlag, Berlin et Heidelberg, 1993 (ISBN 3540940510).[source insuffisante]
- (en) F. Jamil Ragep, Dick Teresi et Roger Hart, « Ancient Roots of Modern Science », Talk of the Nation, National Public Radio, 2000.[Où ?]
- Le couple d'Al-Tusi d'après une copie du XIVe siècle de son manuscrit (Vatican Arabic ms 319, fol. 28v; 13th. c.).
- Djebbar, p. 196.
- Jacques Blamont, Le Chiffre et le songe, Histoire politique de la découverte, éditions Odile Jacob, 1993, p. 166.
- Jacques Blamont, op. cit., p. 167.
- Pierre Duhem, Le système du monde, Histoire des doctrines cosmologiques de Platon à Copernic, Tome II, Hermann, 1914, p. 179 (lire en ligne)
- Pierre Duhem, op. cit., p. 250 et suiv.
- (en) Thomas F. Glick, Medieval science, technology, and medicine: an encyclopedia, Thomas F. Glick, Steven John Livesey, Faith Wallis eds., 2005 (ISBN 9780415969307), p. 478–481.
- (en) Nasir al-Din Tusi, Contemplation and Action: The Spiritual Autobiography of a Muslim Scholar, traduit par Seyyed H. Badakhchani, 1999.[source insuffisante]
- Thomas d'Aquin, Contra Gentiles, lib. 1 cap. 13 n. 14
- On pourrait traduire in moventibus et motis ordinatis par « dans les moteurs et mus sériels (plutôt que sérialisés) »
- St Thomas d'Aquin, Somme Théologique, I, Q110, puis regarder A1, ad 2.
- "Voila, enfin, une preuve indiscutable, quoique tardive et inattendue, que la terre tourne autour du Soleil". L.M. Celnikier, Histoire de l'astronomie, Technique et documentation-Lavoisier, Paris, 1986.
- The Galileo affair
- texte intégral, sur le site internet du Vatican
- Louis Saint-Martin, Sagesse de l'astrologie traditionnelle : Essai sur la nature et les fondements de l'astrologie, L'Harmattan, coll. Théôria, Paris, 2018, p.44 sq.
- « Une critique de la théorie de la relativité par un polytechnicien (X61) »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?) (consulté le )
- « Geocentric theory - Conservapedia »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?) (consulté le )
- Fatal Science Flaws
- Site protestant