Structure from motion
Le principe de Structure from motion (SfM, « Structure acquise à partir d'un mouvement ») est une technique d'imagerie par intervalle (en) photogrammétrique destinée à estimer la structure 3D de quelque chose à partir d'images 2D. Elle combine la vision par ordinateur et la vue humaine. En terme biologique, le SfM désigne le phénomène par lequel une personne (et autres créatures vivantes) peut estimer la structure 3D d'un objet ou d'une scène en mouvement à partir de son champ de vision 2D (rétinien).
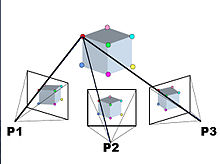
Principe
modifierLes humains perçoivent beaucoup d'informations sur la structure 3D de leur environnement en se déplaçant à l'intérieur de celle-ci. Lorsque l'observateur bouge et que les objets se déplacent, les informations sont obtenues à partir d'images captées au fur et à mesure[1].
Déterminer une structure en se déplaçant pose un problème similaire à celui de trouver une structure avec une vision stéréoscopique. Dans les deux cas, il faut trouver la correspondance entre les images et la reconstruction en 3D de l'objet.
Pour rechercher la correspondance entre les images, les informations telles que les angles (les arêtes avec des dégradés dans plusieurs directions) sont suivies d’une image à l’autre. L’un des détecteurs de caractéristiques les plus largement utilisés est le scale-invariant feature transform (SIFT). Il utilise les maxima d'une pyramide de différence de gaussiennes comme caractéristiques. La première étape du SIFT consiste à trouver une direction de gradient dominante. Pour le rendre invariant en rotation, le descripteur est pivoté pour s'adapter à cette orientation[2]. Un autre détecteur de caractéristique très utilisé est le speeded Up Robust Features (SURF)[3]. Avec celui-ci, la différence de gaussiennes est remplacée par une matrice hessienne basée sur la détection de taches de couleur. De plus, au lieu d'évaluer les histogrammes de gradient, le SURF calcule les sommes des composants de gradient et les valeurs de leurs valeurs absolues[4]. Les caractéristiques détectées à partir de toutes les images seront ensuite mises en correspondance. L’un des algorithmes d’appariement permettant de suivre les caractéristiques d’une image à l’autre est le suiveur de caractéristiques Kanade–Lucas–Tomasi (en)[5].
Parfois, certaines des fonctionnalités correspondantes ne sont pas correctement associées. C'est pourquoi les correspondances doivent également être filtrées. Le RANSAC (RANdom SAmple Consensus) est l'algorithme généralement utilisé pour supprimer les correspondances aberrantes. Dans le document de Fischler et Bolles, le RANSAC est utilisé pour résoudre le « problème de détermination de la localisation », dont l'objectif est de déterminer les points dans l'espace qui se projettent sur une image en un ensemble de points de repère avec des emplacements connus[6].
Les trajectoires des caractéristiques au fil du temps sont ensuite utilisées pour reconstruire leurs positions 3D et le mouvement de la caméra[7]. Une alternative est donnée par les approches dites directes, où les informations géométriques (structure 3D et mouvement de la caméra) sont directement estimées à partir des images, sans abstraction intermédiaire des caractéristiques ou des angles[8].
Il existe plusieurs approches pour structurer à partir du mouvement. En SfM incrémental[9], les poses de caméra sont résolues et ajoutées une à une à la collection. En SfM globale[10],[11], les poses de toutes les caméras sont résolues en même temps. Une approche quelque peu intermédiaire est le SfM d'algorithme de mémoire externe (en), où plusieurs reconstructions partielles sont calculées et ensuite intégrées dans une solution globale.
Applications
modifierTopographie
modifierLa photogrammétrie en Structure from Motion avec stéréoscopie multi-vues fournit des modèles de relief à très grande échelle utilisant des images prises à partir d'une gamme d'appareils photo numériques et éventuellement d'un réseau de points de contrôle au sol. La technique n'est pas limitée en fréquence temporelle et peut fournir des données de nuages de points comparables en densité et en précision à celles générées par le balayage laser terrestre et aérien pour une fraction du coût[12],[13],[14]. Le Structure from motion est également utile dans les environnements éloignés ou difficiles d'accès où le balayage laser terrestre est limité par la portabilité des équipements et le balayage laser aéroporté par la rugosité du terrain, entraînant une perte de données et un raccourcissement de l'image. La technique a été appliquée dans de nombreux contextes tels que les rivières[15], les badlands[16], les côtes sableuses[17],[18], les zones de failles sismiques[19], et les récifs coralliens[20]. Une diversité très différente d'appareils photo numériques peut être utilisée, y compris les reflex numériques, les appareils photo numériques compacts et même les smartphones. En règle générale, cependant, des données plus précises seront obtenues avec des appareils plus coûteux, qui incluent des objectifs de meilleure qualité optique. La technique offre donc des possibilités intéressantes pour caractériser la topographie de surface avec des détails sans précédent et, avec des données multi-temporelles, pour détecter les modifications d'élévation, de position et de volume qui sont symptomatiques des mouvements de la surface de la Terre. Le Structure from Motion peut être placé dans le contexte d'autres méthodes d'arpentage numériques.
Patrimoine culturel
modifierLe SfM peut être utilisé pour estimer correctement le bon état du patrimoine culturel, les efforts de planification et de maintenance, ainsi que les coûts, le contrôle et la restauration. En raison de contraintes sérieuses liées à l'accessibilité des sites et à l'impossibilité d'installer des piliers d'arpentage invasifs, le SfM offre une approche non invasive de la structure, sans interaction directe entre la structure et l'opérateur. L'utilisation est précise car seules des considérations qualitatives sont nécessaires. Il est suffisamment rapide pour répondre aux besoins urgents du monument[21]. La première phase opérationnelle est une préparation précise du levé photogrammétrique où l’établissement de la relation entre la meilleure distance par rapport à l’objet, la distance focale, la distance d’échantillonnage au sol et la résolution du capteur. Avec ces informations, les acquisitions photographiques programmées doivent être effectuées avec un recouvrement vertical d’au moins 60%[22].
Voir aussi
modifierBibliographie
modifier- Jonathan L. Carrivick, Mark W. Smith, Duncan J. Quincey (2016). Structure from Motion in the Geosciences. Wiley-Blackwell. 208 pages. (ISBN 978-1-118-89584-9)
- Richard Hartley et Andrew Zisserman, Multiple View Geometry in Computer Vision, Cambridge University Press, , 655 p. (ISBN 0-521-54051-8, lire en ligne)
- The Geometry of Multiple Images, MIT Press, (ISBN 0-262-06220-8)
- (en) Yi Ma, S. Shankar Sastry, Jana Kosecka et Stefano Soatto, An Invitation to 3-D Vision : From Images to Geometric Models, New York, Springer-Verlag New York, LLC, coll. « Interdisciplinary Applied Mathematics Series, #26 », , 526 p. (ISBN 0-387-00893-4)
Notes et références
modifier- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Structure from motion » (voir la liste des auteurs).
- Linda G. Shapiro et George C. Stockman, Computer Vision, Prentice Hall, , 580 p. (ISBN 0-13-030796-3)
- D. G. Lowe, « Distinctive image features from scale-invariant keypoints », International Journal of Computer Vision, vol. 60, , p. 91–110 (DOI 10.1023/b:visi.0000029664.99615.94)
- H. Bay, T. Tuytelaars et L. Van Gool, « Surf: Speeded up robust features », 9th European Conference on Computer Vision,
- K. Häming et G. Peters, « The structure-from-motion reconstruction pipeline – a survey with focus on short image sequences », Kybernetika, (lire en ligne)
- B. D. Lucas et T. Kanade, « An iterative image registration technique with an application to stereo vision », IJCAI'81 Proceedings of the 7th international joint conference on Artificial intelligence, vol. 2, , p. 674-679 (résumé)
- M. A. Fischler et R. C. Bolles, « Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography », Commun. ACM, vol. 24, , p. 381–395 (DOI 10.1145/358669.358692)
- F. Dellaert, S. Seitz, C. Thorpe et S. Thrun, « Structure from Motion without Correspondence », IEEE Computer Society Conference on Computer Vision and Pattern Recognition, (lire en ligne)
- Jakob Engel, Thomas Schöps et Daniel Cremers « European Conference on Computer Vision (ECCV) 2014 » () (lire en ligne) [PDF]
- J.L. Schönberger et J.M. Frahm, « Structure-from-Motion Revisited », IEEE Computer Society Conference on Computer Vision and Pattern Recognition, (lire en ligne)
- C. Tomasi et T. Kanade, « Shape and motion from image streams under orthography: a factorization method », International Journal of Computer Vision, (lire en ligne)
- V.M. Govindu, « Combining two-view constraints for motion estimation », IEEE Computer Society Conference on Computer Vision and Pattern Recognition, (lire en ligne)
- M. J. Westoby, J. Brasington, N. F. Glasser, M. J. Hambrey et J. M. Reynolds, « ‘Structure-from-Motion’ photogrammetry: A low-cost, effective tool for geoscience applications », Geomorphology, vol. 179, , p. 300–314 (DOI 10.1016/j.geomorph.2012.08.021, lire en ligne)
- (en) M. R. James et S. Robson, « Straightforward reconstruction of 3D surfaces and topography with a camera: Accuracy and geoscience application », Journal of Geophysical Research: Earth Surface, vol. 117, no F3, , F03017 (ISSN 2156-2202, DOI 10.1029/2011jf002289, lire en ligne)
- (en) Mark A. Fonstad, James T. Dietrich, Brittany C. Courville, Jennifer L. Jensen et Patrice E. Carbonneau, « Topographic structure from motion: a new development in photogrammetric measurement », Earth Surface Processes and Landforms, vol. 38, no 4, , p. 421–430 (ISSN 1096-9837, DOI 10.1002/esp.3366, lire en ligne)
- L. Javernick, J. Brasington et B. Caruso, « Modeling the topography of shallow braided rivers using Structure-from-Motion photogrammetry », Geomorphology, vol. 213, , p. 166–182 (DOI 10.1016/j.geomorph.2014.01.006, lire en ligne)
- (en) Mark William Smith et Damià Vericat, « From experimental plots to experimental landscapes: topography, erosion and deposition in sub-humid badlands from Structure-from-Motion photogrammetry », Earth Surface Processes and Landforms, vol. 40, no 12, , p. 1656–1671 (ISSN 1096-9837, DOI 10.1002/esp.3747, lire en ligne)
- (en) Evan B Goldstein, Amber R Oliver, Elsemarie deVries, Laura J Moore et Theo Jass, « Ground control point requirements for structure-from-motion derived topography in low-slope coastal environments », PeerJ PrePrints, (ISSN 2167-9843, DOI 10.7287/peerj.preprints.1444v1, lire en ligne)
- (en) Francesco Mancini, Marco Dubbini, Mario Gattelli, Francesco Stecchi, Stefano Fabbri et Giovanni Gabbianelli, « Using Unmanned Aerial Vehicles (UAV) for High-Resolution Reconstruction of Topography: The Structure from Motion Approach on Coastal Environments », Remote Sensing, vol. 5, no 12, , p. 6880–6898 (DOI 10.3390/rs5126880, lire en ligne)
- Kendra Johnson, Edwin Nissen, Srikanth Saripalli, J. Ramón Arrowsmith, Patrick McGarey, Katherine Scharer, Patrick Williams et Kimberly Blisniuk, « Rapid mapping of ultrafine fault zone topography with structure from motion », Geosphere, vol. 10, no 5, , p. 969–986 (DOI 10.1130/GES01017.1, lire en ligne)
- Mitch Bryson, Stephanie Duce, Dan Harris, Jody M. Webster, Alisha Thompson, Ana Vila-Concejo et Stefan B. Williams, « Geomorphic changes of a coral shingle cay measured using Kite Aerial Photography », Geomorphology, vol. 270, , p. 1–8 (DOI 10.1016/j.geomorph.2016.06.018, lire en ligne)
- Guidi. G.; Beraldin, J.A.; Atzeni, C. High accuracy 3D modelling of cultural heritage: The digitizing of Donatello. IEEE Trans. Image Process. 2004, 13, 370–380
- Kraus, K., 2007. Photogrammetry: Geometry from Image and Laser Scans. Walter de Gruyter, 459 pp. (ISBN 978-3-11-019007-6)