Structure de Weaire-Phelan
| Structure de Weaire–Phelan | |
|---|---|
| |
| Groupe d'espace Notation des fibrifolds |
Pm3n (no 223) 2o |
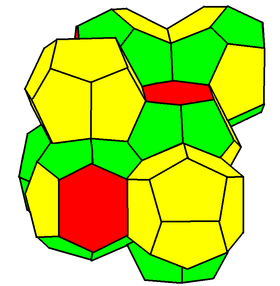
En géométrie, la structure de Weaire–Phelan est une structure tridimensionnelle représentant la structure idéale d'une mousse de bulles d'égal volume. Ce réseau est constitué de polyèdres à faces courbes. En 1993, le physicien Denis Weaire (en) du Trinity College (Dublin) et son élève Robert Phelan ont découvert grâce à des simulations informatiques que cette structure consistait en une meilleure solution du problème de Kelvin que la solution précédemment connue, la structure de Kelvin[1].
La conjecture de Kelvin
modifierEn 1887, Lord Kelvin s'est interrogé sur la manière de partitionner l'espace en cellules d'égal volume telles que l'aire de leur frontière soit la plus faible possible[2]. Ce problème est depuis désigné sous le nom de problème de Kelvin.
Kelvin a proposé comme solution un réseau basé l'octaèdre tronqué, réseau aujourd'hui connu sous le nom de structure de Kelvin. Ce polyèdre à 14 faces (8 faces hexagonales et 6 carrées) permet un pavage de l'espace. Pour se conformer aux conditions de Plateau qui expriment les conditions nécessaires que doit remplir une surface minimale du réseau, les faces hexagonales de la structure doivent être légèrement incurvées.
La conjecture de Kelvin énonce que la structure de Kelvin est la meilleure solution au problème de Kelvin. Cette conjecture a longtemps été considérée comme juste, et aucun contre-exemple n'a été trouvé durant plus de cent ans, jusqu'à la découverte de la structure de Weaire–Phelan.
Description de la structure de Weaire–Phelan
modifierLa structure de Weaire–Phelan diffère de celle Kelvin dans le fait qu'elle utilise deux types de cellules, bien que les deux aient le même volume. Il s'agit de polyèdres déformés par gauchissement de leurs faces.
Le premier type de cellule est le dodécaèdre régulier, de faces pentagonales, qui présente une symétrie tétraédrique (Th). Le second type est un tétrakaidécaèdre irrégulier, le trapézoèdre hexagonal tronqué (en), qui possède deux faces hexagonales et douze pentagonales, et présente une symétrie antiprismatique (D2d).
Tout comme les hexagones dans la structure de Kelvin, les pentagones faisant partie des deux types de polyèdres sont légèrement courbés. L'aire de la surface de la structure de Weaire–Phelan est inférieure de 0,3 % à celle de la structure de Kelvin. Mais il n'est pas encore prouvé que la structure de Weaire–Phelan soit la solution optimale du problème de Kelvin.
Approximation polyédrique
modifierLe réseau polyédrique associé à la structure de Weaire–Phelan (obtenu en aplatissant les faces) est parfois appelé par abus structure de Weaire–Phelan. Il était connu bien avant la découverte de la structure de Weaire–Phelan, mais son intérêt pour le problème de Kelvin n'avait pas été remarqué[3].
Ce réseau se retrouve en cristallographie en tant que structure cristalline où il est appelé "structure de clathrate de type I". Les hydrates de gaz constitués de méthane, propane, et dioxyde de carbone présentent, à faible température, une structure dans laquelle les molécules d'eau se trouvent situées aux nœuds de la structure de Weaire–Phelan et sont liées par des liaisons hydrogène , et les autres molécules se trouvent dans les cellules polygonales.
Certains métaux alcalins comme le siliciure ou le germanium présentent aussi cette structure (Si/Ge aux nœuds, métaux alcalins dans les cellules), tout comme la mélanophlogite (un dioxyde de silicium) (silicium aux nœuds, lié par des atomes d'oxygène sur les arêtes). La mélanophlogite est un dérivé métastable du SiO2 qui se trouve stabilisé dans cette structure car les molécules sont contraintes à rester dans les cellules.
La structure polyédrique de Weaire–Phelan est un des groupes de structures connues sous le nom de phases de Frank–Kasper[4].
Applications
modifierLa structure de Weaire–Phelan a servi d'inspiration pour le design pour le Centre national de natation de Pékin qui a été inauguré à Pékin pour les Jeux olympiques en 2008[5]. La structure du bâtiment qui en résulte est intrinsèquement légère et robuste. Puisque les joints de la structure sont proches des angles qui se retrouvent en géométrie moléculaire tétraédrique, la structure occupe un large espace tout en nécessitant une faible quantité de matière, tout comme c'est le cas de l’hexagone en deux dimensions.
Voir aussi
modifier- Théorème du nid d'abeille, la version en deux dimensions du problème de Kelvin (qui est prouvée).
- Surface minimale
- Bulle de savon
- Conjecture de Kepler
Références
modifier- (en) Denis Weaire et Robert Phelan, « A counter-example to Kelvin's conjecture on minimal surfaces », Philosophical Magazine Letters, vol. 69, , p. 107–110 (DOI 10.1080/09500839408241577).
- (en) Lord Kelvin (Sir William Thomson), « On the Division of Space with Minimum Partitional Area », Philosophical Magazine, vol. 24, no 151, , p. 503 (DOI 10.1080/14786448708628135, lire en ligne).
- On peut trouver un diagramme dans Linus Pauling, The Nature of the Chemical Bond, Cornell University Press, , troisième éd., p. 471
- F. C. Frank et J. S. Kasper, « Complex alloy structures regarded as sphere packings. I. Definitions and basic principles », Acta Crystall., vol. 11,
- Henry Fountain, « A Problem of Bubbles Frames an Olympic Design », New York Times, (lire en ligne).