Somme des angles d'un triangle

En géométrie euclidienne, la somme des angles d'un triangle est égale à l'angle plat, soit 180 degrés ou π radians. Ce résultat est connu et démontré par Euclide, dans ses Éléments.

Deux méridiens sont des "droites" (en géométrie sphérique) perpendiculaires à l'équateur. Dans ce cas, un triangle dont les angles mesurent respectivement 90°, 50° et 90° peut exister. En géométrie euclidienne (voir encadré), ce n'est pas possible : si un triangle possède un angle de 90° et un angle de 50°, le troisième angle doit mesurer 40°.

Il est équivalent à l'axiome des parallèles d'Euclide :

Par un point donné, on peut mener une et une seule parallèle à une droite donnée.

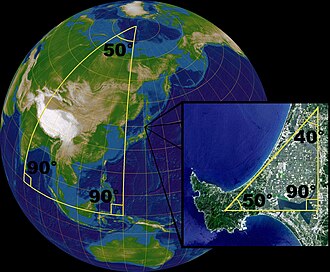
Mais il est possible de construire, tout aussi rigoureusement, d'autres géométries, dites non euclidiennes, qui ne respectent pas cet axiome. La somme des angles d'un triangle n'est alors plus constante, mais elle permet de classifier ces géométries, la valeur de 180° gardant son importance : les géométries pour lesquelles la somme des angles d'un triangle est inférieure à 180° sont dites hyperboliques, celles pour lesquelles elle est supérieure à 180° sont dites elliptiques (comme la géométrie sphérique utilisée pour modéliser la géométrie à la surface de planètes comme la Terre).

En géométrie euclidienne

En géométrie euclidienne (la géométrie souvent considérée comme usuelle) la somme des angles de tout triangle est égale à 180°. Ainsi, la somme des angles est un invariant des triangles, qui permet de résoudre de nombreux problèmes élémentaires de résolution d'un triangle.

Théorème

Lorsqu'on parle de somme des angles d'un triangle, il est d'usage de considérer les mesures des angles géométriques, la proposition s'écrivant de façon plus rigoureuse (mais aussi plus lourde) :

Théorème — La somme des mesures des angles géométriques d'un triangle est égale à la mesure d'un angle plat.

Démonstration

Figure illustrant la démonstration, d'après A. Amiot.

La démonstration classique depuis Euclide repose sur le tracé de la droite parallèle à un côté du triangle et passant par le sommet qui n'appartient pas à ce côté. Ainsi, la propriété sur la somme des angles d'un triangle s'appuie sur l'axiome des parallèles. Différentes rédactions en ont été proposées au cours des siècles. Voici celle que donnait A. Amiot en 1870. Plutôt que de donner comme constante un angle plat, il parle, à la suite d'Euclide lui-même, de « deux angles droits ».

Démonstration classique, rédigée par A. Amiot — Soit le triangle ABC ; je prolonge le côté AB et je mène par le sommet B la ligne droite BE parallèle au côté opposé AC.

Les angles ACB, CBE sont égaux comme alternes-internes par rapport aux parallèles AC, BE et à la sécante BC ; les angles CAB, EBD sont aussi égaux comme correspondants par rapport aux mêmes parallèles et à la sécante AB. Donc, la somme des trois angles ABC, ACB, CAB du triangle est égale à la somme des trois angles adjacents ABC, CBE, EBD formés sur la ligne droite AD, c'est-à-dire qu'elle est égale à deux angles droits.

Cette propriété est un résultat de géométrie euclidienne. Elle n'est pas vérifiée en général en géométrie non euclidienne.

Trois points alignés

La démonstration précédente est valable pour un triangle vrai, défini par trois points non alignés. Mais la propriété est aussi vraie pour un triangle dégénéré constitué de trois points distincts alignés : si trois points A, B et C sont alignés dans cet ordre, les angles du triangle en A et C sont nuls et l'angle en B est plat.

Angles aigus et obtus

Triangle possédant un angle obtus. Les deux autres angles sont alors aigus.

La mesure d'un angle géométrique étant un nombre positif, une première conséquence du théorème de la somme des angles est qu'un triangle ne peut posséder plus d'un angle obtus (c'est-à-dire un angle de mesure supérieure à 90°). En effet, si un triangle possédait deux angles obtus, la somme des mesures de ces deux angles et du troisième angle serait supérieure à 180°.

Triangles particuliers

Un triangle équilatéral est un triangle dont les trois angles ont la même mesure. En notant a cette mesure et en utilisant la somme des angles d'un triangle, il vient :

3a = 180°

Donc

Triangle équilatéral — Les angles d'un triangle équilatéral mesurent 60° (ou encore ^π⁄₃ radians).

Un triangle rectangle isocèle (demi-carré) possède un angle droit (de mesure égale à 90°) et deux angles égaux. En considérant que la somme des angles du triangle, il vient que la somme des deux angles autres que l'angle droit est égale à 180 - 90 = 90°. Comme ils sont égaux, ces deux angles mesurent chacun 45°. Ainsi,

Triangle rectangle isocèle — Les angles d'un triangle rectangle isocèle ont pour mesures respectives 90°, 45° et 45°.

Triangles semblables

Deux triangles semblables.

Deux triangles sont dits semblables lorsqu'ils ont « la même forme », c'est-à-dire lorsque chaque angle de l'un est égal à un angle de l'autre. Cette définition semble indiquer que, pour prouver que deux triangles sont semblables, il faille démontrer trois égalités. Or, en considérant la somme des angles du triangle, deux égalités suffisent : si deux angles a et b d'un premier triangle sont égaux à deux angles d'un autre, ces triangles sont semblables, car les troisièmes angles des deux triangles auront une mesure, en degrés, égale à 180 - (a + b) et seront donc égaux. D'où la propriété :

Triangles semblables — Si deux angles d'un triangle sont égaux à deux angles d'un autre triangle, alors ces triangles sont semblables.

Conséquence pour les polygones

Les 14 façons de décomposer un hexagone convexe en 4 triangles.

Tout polygone simple (c'est-à-dire dont les arêtes ne se croisent pas) à n côtés peut être considéré comme constitué de n – 2 triangles accolés, dont la somme de tous les angles est égale à la somme des angles internes du polygone. C'est l'une des façons de démontrer que la somme des angles internes d'un polygone simple à n côtés est toujours égale à (n – 2)×180°.

En particulier, cette propriété assure que la somme des angles d'un quadrilatère simple est égale à 360°. Si un quadrilatère simple possède trois angles droits, alors son quatrième angle est aussi droit. Le fait que la somme des angles d'un triangle soit égale à deux droits entraîne ainsi l'existence de rectangles en géométrie euclidienne.

Lien avec l'axiome des parallèles

La propriété de géométrie euclidienne doit se lire ainsi : la somme des angles de tout triangle est égale à deux angles droits. Elle se démontre en utilisant le postulat des parallèles, appelé aussi cinquième postulat d'Euclide, qui est :

Axiome des parallèles — Par un point, il passe une et une seule droite parallèle à une droite donnée.

Si on ôte cet axiome de la géométrie euclidienne, on obtient le résultat réciproque suivant, dû à Adrien-Marie Legendre :

Théorème de Legendre — S'il existe un triangle dont la somme des angles est égale à deux angles droits, alors cette somme est la même pour tous les triangles, et le cinquième postulat d'Euclide est vrai.

Autrement dit, il est possible de remplacer le cinquième postulat d'Euclide par un autre axiome : il existe un triangle dont la somme des angles est égale à deux angles droits. Alors, l'axiome des parallèles devient un théorème qu'on peut démontrer. Cette permutation ne change en rien les autres résultats de la géométrie euclidienne.

En géométrie sphérique

Trois points sur une sphère définissent huit triangles sphériques.

On obtient une géométrie cohérente en conservant tous les axiomes de la géométrie euclidienne, sauf l'axiome des parallèles qui devient :

Axiome des parallèles en géométrie sphérique — Étant donnés une droite et un point extérieur à cette droite, il n'existe aucune droite parallèle à cette droite passant par ce point.

Autrement dit, deux droites sont, soit confondues, soit sécantes.

La géométrie sphérique correspond à ces axiomes. Elle est classiquement représentée par la géométrie d'une sphère en géométrie euclidienne, cette sphère correspondant au plan sphérique. Les droites (en géométrie sphérique) sont alors les grands cercles de la sphère, c'est-à-dire les intersections de la sphère avec des plans (au sens euclidien) passant par le centre de la sphère. Un angle entre deux droites sphériques est égal à l'angle formé par les deux plans euclidiens définissant ces droites.

Les résultats sont alors différents de la géométrie euclidienne, en particulier, la somme des angles d'un triangle sphérique n'est plus constante, mais la mesure d'un angle plat (π radians ou 180°) joue néanmoins un grand rôle :

Somme des angles d'un triangle en géométrie sphérique — La somme des angles d'un triangle est toujours supérieure à un angle plat.

La somme des angles d'un triangle sphérique peut varier entre 180 et 540° (entre π et 3π radians). La différence entre la somme des angles d'un triangle et la mesure d'un angle plat est proportionnelle à l'aire S du triangle. Soit, avec des angles exprimés en radians :

$S=({\hat {A}}+{\hat {B}}+{\hat {C}}-\pi )R^{2}$

si la sphère est de rayon R, l'espace euclidien dans lequel elle est plongée étant muni de la distance usuelle.

Un triangle sphérique peut avoir deux ou trois angles droits.

La formule de l'aire montre que, pour un triangle dont l'aire est très proche de zéro, la somme des angles est très proche de l'angle plat. Les résultats de la géométrie euclidienne donnent alors de bonnes approximations de ceux de la géométrie sphérique. En pratique, la géométrie sphérique est utilisée pour l'étude de planètes comme la Terre, notamment pour la navigation. Mais, pour des mesures ou des raisonnements sur des « petites » portions de planète (comme dans un jardin ou une ville peu étendue), la géométrie euclidienne donne des résultats satisfaisants.

En géométrie hyperbolique

Triangle hyperbolique (représenté dans le disque de Poincaré).

La somme des angles d'un triangle hyperbolique est inférieure à pi.

Géométrie hyperbolique#Propriétés métriques

Historique

« Triangle sphérique ». Illustration issue du livre Astronomie populaire de François Arago (1854).

Le résultat donnant la somme des angles d'un triangle (sous-entendu, en géométrie euclidienne) est connu par les anciens Grecs. Suivant les sources, il aurait été découvert par Thalès de Milet (vers 625 - vers 550 av. J.-C.) ou Pythagore (580 - 495 environ). Pythagore ou ses disciples sont aussi réputés, selon Proclus, en avoir rédigé une démonstration. À l'époque d'Aristote (IV^e siècle av. J.-C.), deux démonstrations sont connues. Il fait l'objet de proposition 32 du Livre I des Éléments d'Euclide (vers 300 av. J.-C.), qui en donne une démonstration proche de celle connue par Aristote.

Notes et références

Voir aussi

Bibliographie

• A. Amiot, Éléments de géométrie : rédigés d'après le nouveau programme de l'enseignement scientifique des lycées ; suivis d'un Complément à l'usage des élèves de mathématiques spéciales, Paris, C. Delagrave et Cie, 1870, 428 p. (lire en ligne)
• Michèle Audin, Géométrie, EDP Sciences, coll. « Enseignement sup. Mathématiques », 2006, 420 p. (ISBN 978-2-86883-883-4, lire en ligne)
• Maurice Caveing, La figure et le nombre : recherches sur les premières mathématiques des Grecs, 1997, 424 p. (ISBN 978-2-85939-494-3, lire en ligne)
• Adrien-Marie Legendre, Éléments de géométrie : avec des notes, suivis d'un traite de trigonométrie, Bruxelles, Langlet et Compagnie, 1837 (lire en ligne)
• Nikolaj Ivanovič Lobačevskij, « Pangéométrie ou précis de géométrie fondée sur une théorie générale et rigoureuse des parallèles », dans Œuvres complètes, t. 2 (lire en ligne), p. 615-680
• Henri Lombardi, Géométries élémentaires, vol. 1, Presses Univ. Franche-Comté, 1999, 292 p. (ISBN 978-2-913322-45-5, lire en ligne)
• Daniel Perrin, « Les géométries non euclidiennes », février 2009

Articles connexes

• Théorème de l'angle externe (en)
• Trigonométrie sphérique