Racine carrée de trois

En mathématiques, la racine carrée de trois est le nombre réel positif dont le carré est 3 exactement. Notée ${\sqrt {3}}$ ou 3^1/2, elle vaut approximativement 1,732. Le rationnel 97/56 en est une approximation par excès à $10^{-4}$ près.

Liste de nombres - Nombres irrationnels √2 - φ - √3 - √5 - e - π
La hauteur d'un triangle équilatéral de côté 2 est ${\sqrt {3}}$
Binaire	1.1011101101100111101...
Décimal	1.7320508075688772935...
Hexadécimal	1.BB67AE8584CAA73B...
Fraction continue	$1+{\frac {1}{1+{\frac {1}{2+{\frac {1}{1+{\frac {1}{2+\ldots }}}}}}}}$

Définition, notation et énonciation

• Il existe deux nombres réels opposés dont le carré est 3 ; autrement dit : 3 possède deux racines carrées, opposées. Par convention, la notation ${\sqrt {3}}$ désigne la racine carrée positive de 3, et nécessairement, $-{\sqrt {3}}$ désigne la racine carrée négative de 3. Mais ${\sqrt {3}}$ se lit simplement racine carrée de trois, voire plus simplement racine de trois. Dans le corps des nombres complexes, la notation ${\sqrt {3}}$ désigne la détermination principale de la racine carrée prise au point 3. Le symbole ${\sqrt {\quad }}$ ou $\surd$ s’appelle un radical.
• ${\sqrt {3}}$ se note également $3^{\frac {1}{2}}$, qui se lit trois puissance un demi.
• Dans les langages informatiques, ${\sqrt {3}}$ s'écrit en général sqrt(3), par exemple Math.sqrt(3)en JavaScript.

Irrationalité

La racine carrée de 3 est irrationnelle, comme celle de tout entier naturel qui n'est pas un carré parfait (voir l'article détaillé pour des démonstrations).

Au V^e siècle av. J.-C., Théodore de Cyrène aurait démontré des résultats d'incommensurabilité correspondant à l'irrationnalité des racines carrées des entiers de 3 à 17.

Développement décimal

${\sqrt {3}}=1{,}732~050~8\cdots$ ; ses décimales forment la suite A002194 de l'OEIS.

Dix milliards de décimales ont été calculées en 2013.

On conjecture que, comme tout irrationnel algébrique, ${\sqrt {3}}$ est un nombre normal, à savoir que toute suite finie de décimales consécutives (ou séquence) apparaît avec la même fréquence limite que toute séquence de même longueur.

Développements en fraction continue

Construction de la suite homographique $(u_{n})$ ; les termes d'indice pair croissent vers √3, ceux d'indice impair décroissent vers √3.

La méthode de Bombelli utilisant pour $a>0$ la relation ${\sqrt {3}}=a+{\frac {3-a^{2}}{a+{\sqrt {3}}}}$ permet d'obtenir le développement en fraction continue généralisée : ${\sqrt {3}}=\ a+{\frac {3-a^{2}}{2a+{\frac {3-a^{2}}{2a+{\frac {3-a^{2}}{2a+{\frac {3-a^{2}}{2a+\ldots }}}}}}}}=1+{\frac {3-a^{2}\mid }{\mid 2a}}+{\frac {3-a^{2}\mid }{\mid 2a}}+\cdots$

Pour $a=1$, on obtient :

${\sqrt {3}}=\ 1+{\frac {2}{2+{\frac {2}{2+{\frac {2}{2+{\frac {2}{2+\ldots }}}}}}}}=1+{\frac {2\mid }{\mid 2}}+{\frac {2\mid }{\mid 2}}+\cdots$.

En simplifiant par 2 un étage sur deux on obtient le développement en fraction continue simple de √3 (suite A040001 de l'OEIS) :

${\sqrt {3}}=\ 1+{\frac {1}{1+{\frac {1}{2+{\frac {1}{1+{\frac {1}{2+\ldots }}}}}}}}=[1,1,2,1,2,\dots ]=[1,{\overline {1,2}}]$.

Ce développement est bien périodique (période de longueur 2) comme pour tout irrationnel quadratique (irrationnel solution d'une équation de degré 2 à coefficients entiers), et le théorème de Legendre est bien vérifié.

Les neuf premières réduites communes à ces deux développements sont :$\ u_{0}=1,\ 2,\ {\frac {5}{3}},\ {\frac {7}{4}},\ {\frac {19}{11}},\ {\frac {26}{15}},\ {\frac {71}{41}},\ {\mathbf {\frac {97}{56}}},\ u_{8}={\frac {265}{153}}.$

Comme pour toute fraction continue d’un nombre irrationnel, elles constituent les meilleures approximations de √3.

Elles forment la suite $(u_{n})$, récurrente homographique, définie par : $\ u_{0}=1,\ u_{n+1}=1+{\frac {2}{1+u_{n}}}={\frac {u_{n}+3}{u_{n}+1}}$.

Les deux sous-suites $(u_{2n}){\text{ et }}(u_{2n+1})$ sont adjacentes de limite ${\sqrt {3}}$ et l'on a $u_{2n}<{\sqrt {3}}<u_{2n+1}$.

On en déduit l'encadrement : $\ u_{8}={\frac {265}{153}}<{\sqrt {3}}<{\frac {1351}{780}}=u_{11}$ qui était connu d'Archimède; pour fixer les idées : $\ u_{8}\approx 1{,}732~026\ ;u_{11}\approx 1{,}732~051$.

Le rationnel $u_{n}$ est égal à ${\frac {a_{n}}{b_{n}}}$ où $a_{n},b_{n}$ sont les entiers définis par $(1+{\sqrt {3}})^{n+1}=a_{n}+b_{n}{\sqrt {3}}$, les suites, $(a_{n}),(b_{n})$ étant définies par $a_{0}=b_{0}=1,{\begin{cases}a_{n+1}=a_{n}+3b_{n}\\b_{n+1}=a_{n}+b_{n}\end{cases}}$.

On en déduit les expressions explicites :

• $\forall \ n\geqslant 0,\ u_{n}={\sqrt {3}}{\frac {(1+{\sqrt {3}})^{n+1}+(1-{\sqrt {3}})^{n+1}}{(1+{\sqrt {3}})^{n+1}-(1-{\sqrt {3}})^{n+1}}}$
• $\forall \ n\geqslant 2,\ u_{n}={\frac {\left\lfloor (1+{\sqrt {3}})^{n+1}\right\rceil }{\left\lfloor {\frac {(1+{\sqrt {3}})^{n+1}}{\sqrt {3}}}\right\rceil }}$, où $\left\lfloor x\right\rceil$ signifie l'entier le plus proche de $x$.

Les numérateurs réduits des $u_{n}$ forment la suite A002531 de l'OEIS, et les dénominateurs réduits la suite A002530 de l'OEIS.

La méthode de Bombelli pour $a=2$ conduit à la fraction continue généralisée : ${\sqrt {3}}=2-{\cfrac {1}{4-{\cfrac {1}{4-{\cfrac {1}{4-\ddots }}}}}}=[2,{\overline {-4,4}}]$ dont la suite des réduites est la sous-suite $(u_{2n+1})$ de $(u_{n})$^{[réf. nécessaire]} .

Suite de Héron

La méthode de Héron fournit une suite, dite suite de Héron, qui converge vers la racine carrée d'un nombre réel positif $a$. Quand a = 3 cette suite, convergeant vers √3, est définie par : $\ v_{0}=1,\ v_{n+1}={\frac {v_{n}+{\frac {3}{v_{n}}}}{2}}$.

Ses premiers termes sont : $\ 1,\ 2,\ {\frac {7}{4}},\ v_{3}={\frac {97}{56}}=u_{7}\approx 1{,}7321$ (approximation à 10^-4 près de √3).

Les numérateurs de cette suite forment la suite A002812 de l'OEIS, et ses dénominateurs la suite A071579 de l'OEIS.

La suite $(v_{n})$ est une sous-suite de la suite $(u_{n})$ des réduites de la fraction continue de √3. Plus précisément : $\ v_{n}=u_{(2^{n}-1)}$ .

La suite $(v_{n})$, pour $n\geqslant 1$, décroît rapidement vers √3 (convergence quadratique).

La suite associée $\left({\frac {3}{v_{n}}}\right)$ converge en croissant vers √3 d'où l’encadrement pour tout $n\geqslant 1$ :

${\frac {3}{v_{n}}}<{\sqrt {3}}<v_{n}$.

Méthode de Halley

La méthode de Halley fournit une suite qui croit encore plus rapidement vers √3 (convergence cubique), définie par : $\ w_{0}=1,\ w_{n+1}={\frac {w_{n}(w_{n}^{2}+9)}{3(w_{n}^{2}+1)}}$.

Ses premiers termes sont : $\ 1,\ {\frac {5}{3}},\ w_{2}={\frac {265}{153}}=u_{8}\approx 1{,}7320$.

Les numérateurs de cette suite forment la suite A238799 de l'OEIS.

La suite $(w_{n})$ est une sous-suite de la suite $(u_{n})$ des réduites de la fraction continue de √3. Plus précisément : $\ w_{n}=u_{(3^{n}-1)}$ .

Expression comme somme de série

${\sqrt {3}}=\sum _{n=0}^{\infty }{\frac {\binom {2n}{n}}{6^{n}}}$ ; voir Coefficient binomial central, Série génératrice.

Expressions par radicaux infiniment imbriqués

• $1+{\sqrt {3}}={\sqrt {2+2{\sqrt {2+2{\sqrt {2+\cdots }}}}}}$ ; voir Radical imbriqué, Racine carrée.
• ${\sqrt {3}}={\sqrt[{3}]{3{\sqrt[{3}]{3{\sqrt[{3}]{3\cdots }}}}}}\ ,\$ car $\ {\frac {1}{3}}+{\frac {1}{3^{2}}}+{\frac {1}{3^{3}}}+\cdots ={\frac {1}{2}}$.

En trigonométrie

${\sqrt {3}}$ admet plusieurs expressions trigonométriques :

${\sqrt {3}}=\tan {\frac {\pi }{3}}=\cot {\frac {\pi }{6}}=2\sin {\frac {\pi }{3}}=2\cos {\frac {\pi }{6}}=\ 2-\tan {\frac {\pi }{12}},\quad$ où ${\frac {\pi }{3}},{\frac {\pi }{6}},$ et ${\frac {\pi }{12}}$ sont des angles exprimés en radians $\left({\frac {\pi }{12}}\ \mathrm {rad} =15^{\circ }\right).$

En algèbre

${\sqrt {3}}$ est un nombre algébrique de polynôme minimal $X^{2}-3$, donc un entier quadratique (entier algébrique de degré 2).

Les racines cubiques de l'unité sont : $\ 1,\ {\frac {-1+{\rm {i}}{\sqrt {3}}}{2}}\$ et $\ {\frac {-1-{\rm {i}}{\sqrt {3}}}{2}}.$

En géométrie

• La diagonale d'un cube de côté 1 vaut ${\sqrt {3}}$.
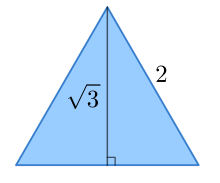
• La hauteur d'un triangle équilatéral de côté 1 vaut ${\sqrt {3}}/2$ . Ceci donne un moyen de construction de ${\sqrt {3}}$ à la règle et au compas. Cette propriété entraîne les suivantes :
  • l'aire d'un triangle équilatéral de côté 1 vaut ${\sqrt {3}}/4$ ; l'aire d'un tétraèdre régulier de côté 1 vaut donc ${\sqrt {3}}$ ;
  • la distance entre deux côtés opposés d'un hexagone régulier de côté 1 vaut ${\sqrt {3}}$ ;
  • ${\sqrt {3}}$ est le rapport des longueurs des diagonales d'un losange d'angles 60° et 120° ;
  • ${\sqrt {3}}$ est le rapport entre la longueur et la largeur de la figure Vesica piscis.

• 
  Diagonale d'un cube unité.
• 
  Proportions entre le côté d'un triangle équilatéral et sa hauteur.
• 
  Hexagone avec ses cotes relatives.
• 
  Vesica piscis avec son losange 60°-120° inscrit : $\ CD/AB={\sqrt {3}}$.

Le rectangle de format (rapport longueur sur largeur) ${\sqrt {3}}$ est étudié dans le cadre de la symétrie dynamique (en). Jay Hambridge (en) en fait l'objet de la leçon 8 de son ouvrage Elements of Dynamic Symmetry et lui donne le nom de root-three rectangle. Lacey Davis Caskey (de) analyse leur présence dans la silhouette de vases grecs, tandis que Rachel Fletcher la recherche dans l'œuvre d'Andrea Palladio. Wolfgang von Wersin (de) en fait le 11^e des 12 rectangles remarquables (les orthogones) qu'il étudie dans son ouvrage Das Buch vom Rechteck: Gesetz und Gestik des Räumlichen. Il lui donne le nom de Sixton. Ce rectangle se construit à partir de la moitié d'un triangle équilatéral et a même aire que celui-ci. Une autre construction possible consiste à partir d'un carré, à construire un rectangle de format ${\sqrt {2}}$ (format A4), servant à construire le rectangle final, il se partage aisément en trois rectangles de même format ${\sqrt {3}}$ et se trouve naturellement inscrit dans un hexagone.

• 
  Construction d'un rectangle de format ${\sqrt {3}}$.
• 
  Découpe du rectangle en trois rectangles de mêmes proportions.
• 
  Rectangle de format ${\sqrt {3}}$ inscrit dans un hexagone.

Voir aussi

• Somme quadratique de Gauss
• Racine carrée d'un entier naturel
• Racine carrée de deux
• Racine carrée de cinq
• Racine carrée de six
• Racine carrée de sept