Problème du partage d'un collier

Le problème du partage d'un collier est le nom imagé donné à plusieurs problèmes semblables en combinatoire et en théorie de la mesure. Son nom et ses solutions sont dus aux mathématiciens Noga Alon^[1] et Douglas West^[2].

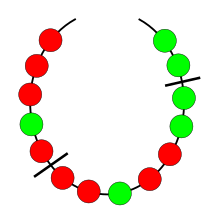
Exemple de partage : k = 2 partenaires, t = 2 couleurs de perles, et 8 perles rouges et 6 vertes. Chaque partenaire reçoit 4 perles rouges et 3 vertes. Une coupe est affichée : l'un des partenaires reçoit la section centrale et l'autre les deux parties restantes.

Description

La formulation de base comprend un collier avec des perles de différentes couleurs. Le collier doit être partagé entre plusieurs partenaires (des « voleurs »), de sorte que chaque partenaire reçoive la même quantité de perles de chaque couleur. De plus, le nombre de « coupes » doit être le plus petit possible (afin de gaspiller le moins possible de métal entre les perles).

Variantes

Le problème admet de nombreuses variantes ; les suivantes ont été décrites et résolues dans l'article original :

Partage discret^[1]^{:Th 1.1} : Le collier contient $k\cdot n$ perles. Les perles sont de $t$ couleurs différentes. Il y a $k\cdot a_{i}$ perles de chaque couleur $i$ , où $a_{i}$ est un entier positif. On cherche à diviser le collier en $k$ parties (pas nécessairement contiguës), dont chacune contient exactement $a_{i}$ perles de couleur i, en effectuant au plus $(k-1)t$ coupes. Le nombre $(k-1)t$ est optimal car si les perles de chaque couleur sont contiguës sur le collier, il faut au moins $k-1$ coupes à l'intérieur de chaque couleur.
Partage continu^[1]^{:Th 2.1} : Le collier est l'intervalle des nombres réels $[0,k\cdot n]$ . Chaque réel de l'intervalle est coloré dans l'une des $t$ couleurs différentes. Pour chaque couleur $i$ , l'ensemble des points colorés en $i$ est mesurable au sens de Lebesgue et de longueur $k\cdot a_{i}$ , où $a_{i}$ est un nombre réel non négatif. On cherche à partitionner l'intervalle en $k$ parties (pas nécessairement contiguës), de sorte que dans chaque partie, la longueur totale de couleur $i$ est exactement $a_{i}$ , le tout en effectuant au maximum $(k-1)t$ coupes.
Partage de mesures^[1]^{:Th 1.2} : Le collier est un intervalle de nombres réels. Il y a $t$ différentes mesures sur l'intervalle, toutes absolument continues par rapport à la longueur. La mesure de l'ensemble du collier, pour la mesure $i$ , est $k\cdot a_{i}$ . On doit partitionner l'intervalle en $k$ parties (pas nécessairement contiguës), de sorte que la mesure de chaque partie, selon la mesure $i$ , est exactement $a_{i}$ . et en effectuant au maximum $(k-1)t$ coupes. Il s'agit d'une généralisation du théorème de Hobby-Rice, et il est utilisé pour obtenir un partage équitable d'un gâteau.

Réduction des variantes

Chacun des problèmes peut être résolu comme suit :

Le partage discret peut ramené à un partage continu, puisqu'un collier discret peut être converti en une coloration de l'intervalle réel $[0,k\cdot n]$ dans laquelle chaque intervalle de longueur 1 est coloré par la couleur de la perle correspondante. Dans le cas où le partage continue essaie de couper à l'intérieur d'une perle, les coupes peuvent être glissées continument de sorte qu'elles ne soient réalisées qu'entre les perles^[1]^{:p. 249}.
Le partage continu peut être ramené à un partage de mesures, puisqu'une coloration d'un intervalle en $t$ couleurs peut être convertie en un ensemble de $t$ mesures telles que la mesure $i$ a pour mesure la longueur totale de la couleur $i$ . L'inverse est également vrai : le partage des mesures peut être résolu par un partage continu, mais en utilisant une réduction plus sophistiquée^[1]^{:p. 252–253}.

Preuves

Le cas $k=2$ peut être prouvé par le théorème de Borsuk-Ulam^[2].

Quand $k$ est un nombre premier impair, la preuve utilise une généralisation du théorème de Borsuk-Ulam^[3].

Quand $k$ est un nombre composé, la preuve est la suivante (illustrée ici pour la variante de partage de mesures). On suppose que $k=p\cdot q$ . Il y a $t$ mesures, dont chacune a la valeur $p\cdot q\cdot a_{i}$ sur le collier entier. En utilisant $(p-1)\cdot t$ coupes, on divise le collier en $p$ parties telles que la mesure $i$ de chaque partie vaut exactement $q\cdot a_{i}$ . En utilisant $(q-1)\cdot t$ coupes, on divise chacune de ces parties en $q$ pièces telles que la mesure $i$ de chaque pièce vaut exactement $a_{i}$ . Il y a alors $pq$ pièces telles que la mesure $i$ de chaque pièce est exactement $a_{i}$ . Le nombre total de coupes est $(p-1)\cdot t$ plus $p(q-1)\cdot t$ , ce qui au total est exactement $(pq-1)\cdot t$ .

Extensions

Colliers aléatoires

Dans certains cas, des colliers aléatoires peuvent être partagés également en utilisant moins de coupes. Noga Alon, Dor Elboim, Gábor Tardos et János Pach^[4] ont étudié le nombre de coupes nécessaires pour partager un collier au hasard entre deux voleurs. Dans le modèle qu'ils ont considéré, un collier est choisi uniformément au hasard parmi l'ensemble des colliers avec t couleurs et m perles de chaque couleur. Lorsque m tend vers l'infini, la probabilité que le collier puisse être divisé en utilisant au plus $\lfloor (t+1)/2\rfloor$ coupes tend vers zéro alors que la probabilité qu'il soit possible de réaliser le partage avec $\lfloor (t+1)/2\rfloor +1$ coupes est bornée et plus grande que zéro. Plus précisément, soit $X=X(t,m)$ le nombre minimal de coupes nécessaires pour diviser le collier. Alors, lorsque $m$ tend vers l'infini, on a :

pour tout $s<(t+1)/2$ :

\mathbb {P} (X=s)=\Theta {\big (}m^{s-(t+1)/2}{\big )}\

pour

s<(t+1)/2

;

\mathbb {P} (X=s)=\Theta (1)\

pour

(t+1)/2<s\leq t

;

\mathbb {P} (X=s)=\Theta {\big (}(\log m)^{-1}{\big )}\

quand

t

est impair et

s=(t+1)/2

.

On peut aussi considérer le cas où le nombre de couleurs tend vers l'infini. Lorsque $m=1$ et que $t$ tend vers l'infini, le nombre de coupes nécessaires est au plus $0,4t$ et au moins $0,22t$ avec une forte probabilité. Il est conjecturé qu'il existe une constante $c$ avec $0,22<c<0,4$ tel que ' $X(t,1)/t$ converge vers $c$ en distribution.

Une coupe de moins

Dans le cas de deux voleurs (donc $k=2$ ) et de $t$ couleurs, un partage équitable nécessite au plus $t$ coupes. Avec seulement $t-1$ coupes, Gábor Simonyi^[5] a montré que les deux voleurs peuvent réaliser un partage « presque équitable » au sens suivant :

Si le collier est constitué de sorte qu'aucune t-coupe n'est possible, alors pour deux sous-ensembles quelconques $D_{1}$ et $D_{2}$ de $\{1,\ldots \,t\}$ disjoints et pas tous deux vides il existe une $t-1$ -coupe telle que :

Pour toute couleur $i\in D_{1}$ , la partition 1 a plus de perles de couleur i que la partition 2 ;
Pour toute couleur $i\in D_{2}$ , la partition 2 a plus de perles de couleur i que la partition 1 ;
Pour une couleur i qui n'appartient à aucune des partitions, les deux partitions ont autant de perles de couleur i .

Cela signifie que si les voleurs ont des préférences sous la forme de deux ensembles de « préférences » $D_{1}$ et $D_{2}$ , non vides tous les deux, il existe une $t-1$ -coupe de sorte que le voleur 1 obtient plus de perles de couleurs dans son ensemble de préférences ' $D_{1}$ que le voleur 2 ; le voleur 2 obtient plus de perles de couleurs dans son jeu de préférences $D_{2}$ que le voleur 1 ; et le partage pour les autres couleurs est égal équitable.

Simonyi attribue à Gábor Tardos le fait d'avoir remarqué que le résultat ci-dessus est une généralisation directe du théorème original du collier d'Alon dans le cas $k=2$ . En effet, soit le collier a une ( $t-1$ )-coupe et il n'y a rien à prouver, soit ce n'est pas le cas, et on peut ajouter des perles d'une couleur fictive au collier et faire en sorte que $D_{1}$ soit composé de la couleur fictive et $D_{2}$ vide. Le résultat de Simonyi montre qu'il alors existe une t -coupe avec le même nombre de perles de chaque couleur réelle.

Un résultat négatif

Pour chaque $k\geq 1$ il existe une $(k+3)$ -coloration mesurable de la droite réelle telle qu'aucun intervalle ne puisse être partagé équitablement en utilisant au plus $k$ coupes^[6].

Partage multidimensionnels

Le résultat peut être généralisé à n mesures de probabilité définies sur un cube de dimension d avec n'importe quelle combinaison de n (k − 1) hyperplans parallèles aux côtés pour k voleurs^[7].

Algorithme d'approximation

Un algorithme d'approximation pour partager un collier peut être dérivé d'un algorithme de réduction de moitié par consensus^[8].

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Necklace splitting problem » (voir la liste des auteurs).

↑ ^{a b c d e et f} Noga Alon, « Splitting Necklaces », Advances in Mathematics, vol. 63, n^o 3,‎ 1987, p. 247-253 (DOI 10.1016/0001-8708(87)90055-7).
↑ ^{a et b} Alon Noga et Douglas B. West, « The Borsuk-Ulam theorem and bisection of necklaces », Proceedings of the American Mathematical Society, vol. 98, n^o 4,‎ décembre 1986, p. 623-628 (DOI 10.1090/s0002-9939-1986-0861764-9).
↑ I. Barany, S.B. Shlosman et A. Szucs, « On a topological generalization of a theorem of Tverberg », Journal of the London Mathematical Society, vol. 2, n^o 23,‎ 1981, p. 158–164 (DOI 10.1112/jlms/s2-23.1.158, CiteSeer^x 10.1.1.640.1540).
↑ Noga Alon, Dor Elboim, Gábor Tardos et János Pach, « Random Necklaces require fewer cuts », Arxiv,‎ 2021 (arXiv 2112.14488)
↑ Gábor Simonyi, « Necklace bisection with one cut less than needed », Electronic Journal of Combinatorics, vol. 15, n^o N16,‎ 2008 (DOI 10.37236/891).
↑ Noga Alon, « Splitting necklaces and measurable colorings of the real line », Proceedings of the American Mathematical Society, vol. 137, n^o 5,‎ 25 novembre 2008, p. 1593–1599 (ISSN 1088-6826, DOI 10.1090/s0002-9939-08-09699-8, arXiv 1412.7996).
↑ Mark de Longueville et Rade T. Živaljević, « Splitting multidimensional necklaces », Advances in Mathematics, vol. 218, n^o 3,‎ 2008, p. 926-939 (DOI 10.1016/j.aim.2008.02.003, arXiv math/0610800).
↑ Forest W. Simmons et Francis Edward Su, « Consensus-halving via theorems of Borsuk-Ulam and Tucker », Mathematical Social Sciences, vol. 45, n^o 1,‎ février 2003, p. 15–25 (DOI 10.1016/s0165-4896(02)00087-2, CiteSeer^x 10.1.1.203.1189).

Annexes

Bibliographie

Noga Alon et Andrei Graur, « Efficient splitting of necklaces », 48th International Colloquium on Automata, Languages, and Programming (ICALP 2021), Schloss Dagstuhl-Leibniz-Zentrum für Informatik, vol. LIPIcs 198,‎ 2021, p. 14:1-14:17.
Aris Filos-Ratsikas et Paul W. Goldberg, « The complexity of necklace splitting, consensus-halving, and discrete ham sandwich », Proceedings STOC,‎ 2019, p. 638-649 (DOI 10.1145/3313276.3316334, arXiv 1805.12559).
Duško Jojić, Gaiane Panina et Rade Živaljević, « Splitting Necklaces, with Constraints », SIAM Journal on Discrete Mathematics, vol. 35, n^o 2,‎ janvier 2021, p. 1268–1286 (DOI 10.1137/20M1331949, arXiv 1907.09740).

Articles liés

Liens externes

[vidéo] « "Sneaky Topology" », sur YouTube, une vidéo d'introduction présentant entre autres le problème et sa solution topologique.

[Alon_1987-1] {a b c d e et f} Noga Alon, « Splitting Necklaces », Advances in Mathematics, vol. 63, n^o 3,‎ 1987, p. 247-253 (DOI 10.1016/0001-8708(87)90055-7).

[Alon_1986-2] {a et b} Alon Noga et Douglas B. West, « The Borsuk-Ulam theorem and bisection of necklaces », Proceedings of the American Mathematical Society, vol. 98, n^o 4,‎ décembre 1986, p. 623-628 (DOI 10.1090/s0002-9939-1986-0861764-9).

[BSS-3] I. Barany, S.B. Shlosman et A. Szucs, « On a topological generalization of a theorem of Tverberg », Journal of the London Mathematical Society, vol. 2, n^o 23,‎ 1981, p. 158–164 (DOI 10.1112/jlms/s2-23.1.158, CiteSeer^x 10.1.1.640.1540).

[4] Noga Alon, Dor Elboim, Gábor Tardos et János Pach, « Random Necklaces require fewer cuts », Arxiv,‎ 2021 (arXiv 2112.14488)

[Simonyi_2008-5] Gábor Simonyi, « Necklace bisection with one cut less than needed », Electronic Journal of Combinatorics, vol. 15, n^o N16,‎ 2008 (DOI 10.37236/891).

[6] Noga Alon, « Splitting necklaces and measurable colorings of the real line », Proceedings of the American Mathematical Society, vol. 137, n^o 5,‎ 25 novembre 2008, p. 1593–1599 (ISSN 1088-6826, DOI 10.1090/s0002-9939-08-09699-8, arXiv 1412.7996).

[7] Mark de Longueville et Rade T. Živaljević, « Splitting multidimensional necklaces », Advances in Mathematics, vol. 218, n^o 3,‎ 2008, p. 926-939 (DOI 10.1016/j.aim.2008.02.003, arXiv math/0610800).

[8] Forest W. Simmons et Francis Edward Su, « Consensus-halving via theorems of Borsuk-Ulam and Tucker », Mathematical Social Sciences, vol. 45, n^o 1,‎ février 2003, p. 15–25 (DOI 10.1016/s0165-4896(02)00087-2, CiteSeer^x 10.1.1.203.1189).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]