Numberlink
Numberlink est une famille de puzzles logiques dans laquelle le but est de relier des nombres sur une grille.
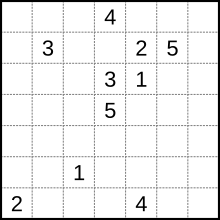

Règles
modifierL'objectif est de tracer un chemin entre toutes les paires de mêmes nombres sur une grille. Les chemins ne doivent pas se croiser. Les nombres doivent être aux extrémités des chemins (pas en plein milieu). Généralement, on demande que toutes les cases de la grille soient remplies..
Histoire
modifierLa plus ancienne référence à un puzzle de type Numberlink remonte à 1897, dans une publication de Sam Loyd[1], un concepteur américain de casse-tête mathématiques et logiques. C’est cependant après la publication de ce jeu par l’éditeur Nikoli que ce type de puzzle gagne en popularité[2].
Résolution algorithmique
modifierRéduction à SAT
modifierLe problème Numberlink peut se réduire à une résolution du problème SAT[3]. On peut alors utiliser un solveur SAT pour trouver une solution.
Recherche de plus court chemin
modifierUne autre approche possible est de chercher un plus court chemin entre l’état de départ (la grille non remplie) et un état final, c’est-à-dire lorsque le puzzle est résolu. On peut alors utiliser la variété d’algorithmes de parcours de graphes[4].
NP-complétude
modifierIl a été prouvé pour la plupart des versions de règles du jeu Numberlink que ce problème est NP-complet[2].
Références
modifier- Sam Lyod, « Sam Loyd’s puzzles: The fuzzled neighbors. », The Brooklyn Daily Eagle, , p. 26
- Aaron Adcock1, Erik D. Demaine, Martin L. Demaine, Michael P. O’Brien, Felix Reidl, Fernando Sánchez Villaamil et Blair D. Sullivan, « Zig-Zag Numberlink is NP-Complete », Stanford University, (lire en ligne [PDF])
- (en) Vincent Pilaud, « NUMBERLINK SOLVER » [PDF], sur polytechnique (consulté le )
- (en) Matt Zucker, « Flow Free solver », sur Needlessly complex, (consulté le )