Nombre de Schröder-Hipparque

En théorie des nombres, les nombres de Schröder-Hipparque forment une suite d'entiers qui servent à compter les arbres planaires avec un ensemble donné de feuilles, les insertions de parenthèses dans une suite, et le nombre de façons de découper un polygone convexe en polygones plus petits par l'insertion de diagonales. Cette suite de nombres commence par

Les onze subdivisions d'un pentagone.

1, 1, 3, 11, 45, 197, 903, 4279, 20793, 103049, 518859,... (c'est la suite A001003 de l'OEIS).

Ils sont aussi appelés nombres super-Catalans, petits nombres de Schröder, ou nombres d'Hipparque, d'après Eugène Charles Catalan et ses nombres de Catalan, Ernst Schröder et ses (grands) nombres de Schröder très voisins, et d'après le mathématicien et astronome grec Hipparque qui, selon Plutarque, connaissait certainement ces nombres.

Applications en combinatoire énumérative

Équivalence combinatoire entre subdivisions de polygones, arbres planaires et parenthésages. Le mot est (ab(cdef))g.

Les nombres de Schröder-Hipparque peuvent servir à dénombrer des objets combinatoires dont on sait par ailleurs qu'ils sont étroitement reliés  :

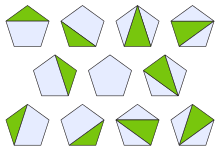
• Le n-ième nombre de la suite est le nombre de subdivisions d'un polygone à n + 1 côtés en polygones plus petits par l'adjonction de diagonales au polygone de départ.
• Le n-ième nombre est le nombre d'arbres planaires à n feuilles, et dont les nœuds internes ont deux enfants ou plus.
• Le n-ième nombre est aussi le nombre de façons d'insérer des parenthèses dans une suite de n symboles, de sorte que toute paire de parenthèses entoure au moins deux symboles ou groupes parenthésés, et sans paire de parenthèses entourant la suite tout entière.
• Le n-ième nombre donne enfin aussi le nombre de faces, de toute dimension, d'un associaèdre K_n + 1, de dimension n − 1, y compris l'associaèdre lui-même vue comme une face, mais sans compter l'ensemble vide. Par exemple, l'associaèdre K₄, de dimension 2, est un pentagone; il a cinq sommets et cinq arêtes, ce qui donne, avec l'associaèdre lui-même, un total de 11 faces.

La figure illustre la bijection combinatoire simple entre ces objets : une subdivision d'un polygone est représenté par un arbre planaire qui est son graphe dual. Les feuilles de l'arbre sont en bijection avec les symboles de la suite représentée, et les nœuds internes, à l'exception de la racine, représentent des groupes parenthésés. La suite des parenthèses elle-même peut s'inscrire sur le contour du polygone : les symboles sont sur les côtés et les parenthèses délimitent les extrémités des diagonales : la parenthèse est ouvrante à la première rencontre, et fermante à la deuxième. Cette équivalence donne une preuve par bijection du fait que tous ces objets sont énumérés par une même suite d'entiers.

La même suite dénombre aussi les permutations doubles (en) (ce sont des suites d'entiers de 1 à n où chaque nombre apparaît deux fois, avec les premières occurrences de chaque nombre en ordre croissant) qui évitent les motifs de permutation 12312 et 121323.

D'autres interprétations sont données dans Stanley 1999, vol. 2, Exercice 6.39.

Suites voisines

• Les nombres de Schröder ou grands nombres de Schröder sont juste le double des nombres de Schröder-Hipparque, et comptent divers types d'objets combinatoire parmi lesquels certaines familles de chemins dans des grilles, les partitions de rectangles en rectangles plus petits par des découpes en tranches verticales ou horizontales, des parenthésages où on autorise aussi une paire de parenthèses autour la suite entière.
• Les nombres de Catalan aussi comptent des ensembles similaires d'objets, parmi lesquels les triangulations de polygones convexes, les arbres binaires (dont les nœuds internes ont exactement deux enfants), ou les parenthésages dans lesquels toute paire de parenthèses entoure exactement deux symboles ou groupes parenthésés.
• On peut faire un parallèle entre les associaèdres et les permutoèdres (en) : les nombres de Schröder-Hipparque comptent les faces et les nombres de Catalan les sommets d'un associaèdre; les nombres correspondants pour le permutoèdre sont les nombres de Bell ordonnés et les factorielles.

Expressions

La suite des nombres de Catalan et la suite des nombres de Schröder-Hipparque peuvent être vues comme des vecteurs. Ils sont alors les seuls vecteurs propres pour les deux premiers opérateurs d'une famille d'opérateurs linéaires sur les suites d'entiers. La k-ième suite dans cette famille de suites d'entiers est la suite

$x_{1},x_{2},\ldots ,x_{n},\ldots$

où les $x_{n}$ sont obtenus comme la somme des nombres de Narayana multipliés par les puissances de k :

$x_{n}=\sum _{i=1}^{n}N(n,i)\,k^{i-1}=\sum _{i=1}^{n}{\frac {1}{n}}{n \choose i}{n \choose i-1}k^{i-1}.$

Si l'on pose $k=1$ dans cette formule, on obtient les nombres de Catalan, et pour $k=2$, la formule donne les nombres de Schröder-Hipparque.

Relation de récurrence

De manière équivalant à la formule sommatoire ci-dessus, les nombres de Schröder-Hipparque peuvent aussi bien être définis par une relation de récurrence :

$s(n)={\frac {1}{n}}{\Big (}(6n-9)s(n-1)-(n-3)s(n-2){\Big )}.$

Stanley en donne une preuve par les séries génératrices. Cette série est

$\sum s(n)x^{n}={\frac {1}{4}}{\Big (}1+x-{\sqrt {1-6x+x^{2}}}{\Big )}.$

Foata et Zeilberger en donnent une preuve combinatoire directe.

Historique

D'après une ligne dans les Propos de table de Plutarque, Hipparque savait que le nombre de « propositions composées positives » que l'on peut former à partir de dix propositions simples est 103 049, et que le nombre de propositions négatives est 310 952. Cette affirmation est restée inexpliquée jusqu'en 1994, quand David Hough, un étudiant diplômé de l'université George-Washington, a observé qu'il y a 103 049 façons de parenthéser une suite de dix éléments. Une explication semblable peut être donnée pour le deuxième nombre : il est très proche de (103049 + 518859)/2 = 310954 qui est la moyenne des dixième et onzième nombres de Schröder-Hipparque, et qui compte le nombre de parenthésages de dix termes avec un signe.

En mathématiques modernes, le problème de compter les divers parenthésages a été introduit par Schröder 1870.

Notes et références

Notes

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Schröder–Hipparchus number » (voir la liste des auteurs).

Références

• (en) F. Acerbi, « On the shoulders of Hipparchus: A reappraisal of ancient Greek combinatorics », Arch. Hist. Exact Sci., vol. 57,‎ 2003, p. 465-502 (lire en ligne [archive du 21 juillet 2011]).
• (en) M. Bernstein et Neil Sloane, « Some canonical sequences of integers », Linear Algebra Appl., vol. 226/228,‎ 1995, p. 57-72 (DOI 10.1016/0024-3795(94)00245-9, MR 1344554).
• (en) William Y. C. Chen, Toufik Mansour et Sherry H. F. Yan, « Matchings avoiding partial patterns », Electronic Journal of Combinatorics, vol. 13, n^o 1,‎ 2006, article n^o 112(electronic) (MR 2274327, lire en ligne).
• (en) Curtis Coker, « A family of eigensequences », Discrete Math., vol. 282, n^os 1-3,‎ 2004, p. 249-250 (DOI 10.1016/j.disc.2003.12.008, MR 2059525).
• (en) Ivor M. H. Etherington, « Some problems of non-associative combinations (I) », Edinburgh Mathematical Notes, vol. 32,‎ 1940, p. 1-6 (DOI 10.1017/S0950184300002639).
• (en) Dominique Foata et Doron Zeilberger, « A classic proof of a recurrence for a very classical sequence », J. Combin. Theory Ser. A, vol. 80, n^o 2,‎ 1997, p. 380-384 (DOI 10.1006/jcta.1997.2814, MR 1485153, arXiv math/9805015).
• (en) Ralf Holtkamp, « On Hopf algebra structures over free operads », Adv. Math., vol. 207, n^o 2,‎ 2006, p. 544-565 (DOI 10.1016/j.aim.2005.12.004, MR 2271016, arXiv math/0407074).
• (en) Ernst Schröder, « Vier combinatorische Probleme », Z. Angew. Math. Phys., vol. 15,‎ 1870, p. 361-376.
• (en) Louis W. Shapiro et Robert A. Sulanke, « Bijections for the Schröder numbers », Mathematics Magazine, vol. 73, n^o 5,‎ 2000, p. 369-376 (DOI 10.2307/2690814, MR 1805263).
• (en) Richard P. Stanley, « Hipparchus, Plutarch, Schröder, and Hough », Amer. Math. Monthly, vol. 104, n^o 4,‎ 1997a, p. 344-350 (DOI 10.2307/2974582, MR 1450667, lire en ligne).
• (en) Richard P. Stanley, Enumerative Combinatorics, vol. 1, Cambridge/New York/Melbourne etc., Cambridge University Press, coll. « Cambridge Studies in Advanced Mathematics » (n^o 49), 1997b, 2^e éd. (ISBN 978-0-521-55309-4 et 0-521-55309-1, présentation en ligne).
• (en) Richard P. Stanley, Enumerative Combinatorics, vol. 2, Cambridge/New York/Melbourne etc., Cambridge University Press, coll. « Cambridge Studies in Advanced Mathematics » (n^o 62), 1999, 585 p. (ISBN 0-521-56069-1, présentation en ligne).

Voir aussi

Articles connexes

• Subdivision d'un polygone

Liens externes

• (en) Eric W. Weisstein, « Super Catalan Number », sur MathWorld
• « The Hipparchus Operad », The n-Category Café, 1^er avril 2013.