Méthode du vecteur spatial

La méthode du vecteur spatial (Space vector modulation en anglais et souvent abrégé SVM ou SVPWM) est un algorithme utilisé pour réaliser la Modulation de largeur d'impulsion (MLI). Elle sert dans les onduleurs à produire la tension alternative à partir d'une tension continue. Elle est principalement utilisée pour les machines électriques tournantes. L'un des objectifs de la méthode est d'obtenir un bon compromis entre la réduction du contenu harmonique de la tension produite et la réduction des pertes par commutations. Elle est intimement liée à la transformation de Clarke^[1].

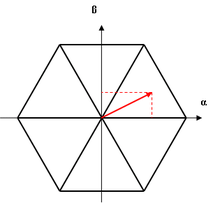
Principe

Hypothèses

Onduleur triphasé en tout ou rien

Un onduleur triphasé comme représenté ci-contre permet de créer une tension alternative triphasée, par exemple pour alimenter un moteur électrique, à partir d'une tension continue.

À aucun moment, il ne faut que deux interrupteurs en série (par exemple A- et A+) soient fermés simultanément sous peine de court-circuit. En supposant qu'au moins un des interrupteur en série est toujours ouvert, on obtient huit états possibles. On note par un « 1 » l'état quand l'interrupteur du haut est fermé et par un « 0 » l'état lorsque celui du bas est fermé^[2]:

Vecteur	A⁺	B⁺	C⁺	A⁻	B⁻	C⁻	V_AB	V_BC	V_CA
U₀ = {000}	OFF	OFF	OFF	ON	ON	ON	0	0	0	vecteur de roue libre
U₁ = {100}	ON	OFF	OFF	OFF	ON	ON	+V_dc	0	−V_dc	vecteur actif
U₂ = {110}	ON	ON	OFF	OFF	OFF	ON	0	+V_dc	−V_dc	vecteur actif
U₃ = {010}	OFF	ON	OFF	ON	OFF	ON	−V_dc	+V_dc	0	vecteur actif
U₄ = {011}	OFF	ON	ON	ON	OFF	OFF	−V_dc	0	+V_dc	vecteur actif
U₅ = {001}	OFF	OFF	ON	ON	ON	OFF	0	−V_dc	+V_dc	vecteur actif
U₆ = {101}	ON	OFF	ON	OFF	ON	OFF	+V_dc	−V_dc	0	vecteur actif
U₇ = {111}	ON	ON	ON	OFF	OFF	OFF	0	0	0	vecteur de roue libre

On note qu'en parcourant périodiquement les états de U₁ à U₆, les trois phases obtenues sont distantes d'un angle de 120°, comme dans un système triphasé^[2]. Toutefois, cette simple succession d'états ne permet pas d'avoir une forme d'onde sinusoïdale satisfaisante.

Schéma explicatif de la méthode du vecteur spatial. La tension de consigne est V_ref. Le cercle de rayon V_{ref_MAX} est la valeur maximale prise par la tension de sortie sans surmodulation

Modulation

Réglage de l'angle

L'alternance des tensions U₁ et U₂ permet de créer en moyenne la tension U_a

La tension alternative produite par l'onduleur permet d'alimenter une machine tournante et d'en déterminer le flux.

La modulation de largeur d'onde permet de produire un vecteur quelconque U_a (voir ci-contre) en appliquant alternativement les tensions proches (ici U₁ et U₂). Les enroulements du stator de la machine tournante étant fortement inductifs, le courant est lissé. La machine se comporte donc comme si elle recevait réellement la tension U_a^[2].

La logique de l'algorithme commence par déterminer dans lequel des six secteurs la tension souhaitée se trouve afin de sélectionner les deux tensions à utiliser. La durée d'application de chacune des tensions permet de régler précisément l'angle de la tension résultante^[2].

Afin d'avoir une tension sinusoïdale de fréquence f, la tension souhaitée tourne dans le repère à la même fréquence.

Réglage de l'amplitude

Le passage par le vecteur de roue libre permet de réduire l'amplitude

En utilisant uniquement les états allant de U₁ à U₆, on obtient une tension résultante maximale. Afin de réduire l'amplitude, ce qui est souhaitable pour la commande d'une machine tournante, des passages par les vecteurs de roue libre, U₀ ou U₇, sont insérés dans la suite des commutations. Dans l'exemple ci-contre, le temps passé dans l'état U₁ relativement à celui passé dans l'état U₂ est constant quelle que soit l'amplitude. Ce rapport réglant l'angle. Le passage plus ou moins long par le vecteur de roue libre permet de réduire l'amplitude. Une période de commutation alterne donc trois états : deux vecteurs actifs et un vecteur de roue libre^[2].

Quantification du réglage

Grâce à la connaissance de l'amplitude du vecteur désiré dans le repère complexe $\alpha \beta$ , il est possible de calculer le temps d'utilisation effectif de chaque vecteur réalisable par l'onduleur afin d'implémenter en pratique cette stratégie. Une proposition de détermination par le calcul est proposé ci-dessous^[1].

Détermination des temps d'utilisation

Comme précisé précédemment, l'objectif est de calculer les temps d'utilisation de chaque vecteur. Ce temps d'utilisation, pour le secteur $k$ est noté $T_{U_{k}}$ .

Ainsi, pour représenter une tension dans le secteur $k$ , il est nécessaire de calculer $T_{U_{0}}$ $T_{U_{k}}$ , $T_{U_{k+1}}$ et $T_{U_{7}}$ (Respectivement, le temps de calcul de la première moitié de la séquence nulle de tension, du vecteur $k$ , du vecteur $k+1$ et la seconde moitié de la séquence nulle de tension).

Ainsi, il va falloir jouer avec le temps d'utilisation de chaque vecteur afin de réaliser la tension désirée notée $\mathbf {U} _{ref}$ . Ce calcul va pouvoir être réalisé grâce à la relation de Chasles grâce au temps d'utilisation de chaque vecteur et à l'amplitude de chaque vecteur.

Afin de réaliser ce calcul plusieurs hypothèses sont requises.

La première, est que pour une période d'échantillonnage donnée, la commande réalisée doit être symétrique. C'est-à-dire que sur une période d'échantillonnage $T_{s}$ , la première moitié (de $t=0$ à $t={\frac {T_{s}}{2}}$ ) est répétée symétriquement par rapport à ${\frac {T_{s}}{2}}$ sur la deuxième moitié (c-à-d de $t={\frac {T_{s}}{2}}$ à $t=T_{s}$ ). Ainsi par exemple, pour le premier secteur la séquence obtenue sera : $\mathbf {U} _{0}\mathbf {U} _{1}\mathbf {U} _{2}\mathbf {U} _{7}\mathbf {U} _{7}\mathbf {U} _{2}\mathbf {U} _{1}\mathbf {U} _{0}$ .

La deuxième hypothèse est que l'utilisation des vecteurs nuls de tension doit être identique c'est-à-dire que $T_{U_{0}}=T_{U_{7}}$

Enfin la dernière hypothèse (bien qu'évidente) est que la somme des temps d'utilisation doit être confinée à une période d'échantillonnage, ainsi: $T_{U_{0}}+T_{U_{k}}+T_{U_{k+1}}+T_{U_{7}}=T_{s}$

Dans le plan complexe, on notera $\mathbf {U} _{ref}=V_{r}e^{i\,\phi }=V_{r}\cos(\phi )+iV_{r}\sin(\phi )$ . $i$ étant la variable complexe.

Sachant que les vecteurs nuls sont $\mathbf {U_{0}} =0$ et que $\mathbf {U_{7}} =0$ , et ce quel que soit le moment où le secteur considéré, ils n'ont pas besoin d'être représentés dans la relation de Chasles exprimant $\mathbf {U} _{ref}$ ci-après. On cherche donc à exprimer la tension de référence comme suit:

$\mathbf {U} _{ref}={\frac {T_{U_{k}}}{T_{s}}}\mathbf {U} _{k}+{\frac {T_{U_{k+1}}}{T_{s}}}\mathbf {U} _{k+1}$

Ainsi, l'équation précédente peut être écrite:

$V_{r}e^{i\phi }={\frac {2}{3}}{\frac {1}{T_{s}}}V_{DC}e^{i\,k{\frac {\pi }{3}}}\left(T_{U_{k}}e^{-i{\frac {\pi }{3}}}+T_{U_{k+1}}\right)$

Avec $V_{DC}$ la tension de bus continu. En projetant l'équation précédente sur l'axe des réels et sur l'axe des complexes, on obtient:

${\frac {3}{2}}{\frac {V_{r}}{V_{DC}}}T_{s}\cos(\phi )=\cos \left(\left(k-1\right){\frac {\pi }{3}}\right)T_{U_{k}}+\cos \left(k{\frac {\pi }{3}}\right)T_{U_{k+1}}$

${\frac {3}{2}}{\frac {V_{r}}{V_{DC}}}T_{s}\sin(\phi )=\sin \left(\left(k-1\right){\frac {\pi }{3}}\right)T_{U_{k}}+\sin \left(k{\frac {\pi }{3}}\right)T_{U_{k+1}}$

Ce qui mène après simplifications à:

$T_{U_{k}}={\sqrt {3}}{\frac {V_{r}}{V_{DC}}}T_{s}\cos \left(\phi +\left(3-2k\right){\frac {\pi }{6}}\right)$

$T_{U_{k+1}}={\sqrt {3}}{\frac {V_{r}}{V_{DC}}}T_{s}\sin \left(\phi +\left(2-2k\right){\frac {\pi }{6}}\right)$

Or, comme $T_{U_{0}}+T_{U_{7}}+T_{U_{k}}+T_{U_{k+1}}=T_{s}$ et que $T_{U_{0}}=T_{U_{7}}$ , alors:

$T_{U_{0}}={\frac {T_{s}-T_{U_{k}}-T_{U_{k+1}}}{2}}$

Ainsi:

$T_{U_{0}}={\frac {T_{s}}{2}}\left[1-{\sqrt {3}}{\frac {V_{r}}{V_{DC}}}\cos \left(\phi -\left(2k-1\right){\frac {\pi }{6}}\right)\right]$

Maintenant que les temps des quatre vecteurs nécessaires à la réalisation de la tension sont connus, dans le cas d'une implémentation réelle, il faudra porter une attention particulière à l'adjacence des vecteurs (en effet l'ordre des vecteurs importe peu, au vu du calcul précédent qui n'en fait pas intervenir l'ordre). Ainsi, la séquence sera pour chaque secteur:

Secteur 1: $\mathbf {U} _{0}\mathbf {U} _{1}\mathbf {U} _{2}\mathbf {U} _{7}\mathbf {U} _{7}\mathbf {U} _{2}\mathbf {U} _{1}\mathbf {U} _{0}$
Secteur 2: $\mathbf {U} _{0}\mathbf {U} _{3}\mathbf {U} _{2}\mathbf {U} _{7}\mathbf {U} _{7}\mathbf {U} _{2}\mathbf {U} _{3}\mathbf {U} _{0}$
Secteur 3: $\mathbf {U} _{0}\mathbf {U} _{3}\mathbf {U} _{4}\mathbf {U} _{7}\mathbf {U} _{7}\mathbf {U} _{4}\mathbf {U} _{3}\mathbf {U} _{0}$
Secteur 4: $\mathbf {U} _{0}\mathbf {U} _{5}\mathbf {U} _{4}\mathbf {U} _{7}\mathbf {U} _{7}\mathbf {U} _{4}\mathbf {U} _{5}\mathbf {U} _{0}$
Secteur 5: $\mathbf {U} _{0}\mathbf {U} _{5}\mathbf {U} _{6}\mathbf {U} _{7}\mathbf {U} _{7}\mathbf {U} _{6}\mathbf {U} _{5}\mathbf {U} _{0}$
Secteur 6: $\mathbf {U} _{0}\mathbf {U} _{1}\mathbf {U} _{6}\mathbf {U} _{7}\mathbf {U} _{7}\mathbf {U} _{6}\mathbf {U} _{1}\mathbf {U} _{0}$

Optimisation et surmodulation

Afin d'améliorer la forme de la tension résultante, il est possible d'appliquer le vecteur de roue libre deux fois au lieu d'une durant une période, avant et après chaque passage par un vecteur actif. La durée totale de son application restant la même.

Afin d'avoir une tension de forme sinusoïdale, la tension résultante doit rester dans le cercle de rayon ${\frac {\sqrt {3}}{2}}$ dessiné. Toutefois, de manière transitoire, il est possible d'en sortir, en allant dans les coins, afin de produire un moment important dans le moteur. On parle de surmodulation. La tension n'est donc plus sinusoïdale, elle présente un contenu harmonique important qui entraîne des pertes plus élevées ^[1].

La SVM Optimisée

Plus récemment, la SVM optimisée a fait son apparition dont le principe est de ne plus considérer les secteurs de la SVM comme étant de taille égale et constant mais comme étant variables. Des méthodes d'optimisation sont alors employées afin de choisir la taille des secteurs. L'optimisation est classiquement faite de manière à minimiser le WTHD, qui a pour avantage de ne pas dépendre de la charge considérée.

D'autres travaux basés sur une représentation vectorielle, montre un avantage substantiel à changer de paradigme. Ainsi la Near-state PWM est apparue permettant de diminuer la tension de mode commun et ainsi améliorer la compatibilité électromagnétique ^[3].

Lien avec les MLI intersectives

Il est possible de démontrer que la SVM classique peut se ramener à une MLI intersective par injection d'harmoniques dans la modulante (ou ajout d'une tension de mode commun) à la tension de référence^[4]^,^[5]. La tension de mode commun à ajouter est alors égale à : $v_{0}=-{\frac {\max(\mathbf {U} _{ref})+\min(\mathbf {U} _{ref})}{2}}=-V_{med}$ .

Avec $\mathbf {U} _{ref}$ , le vecteur de tension de référence noté : $\mathbf {U} _{ref}=mV_{DC}[\sin(\omega t),\sin(\omega t-{\frac {2\pi }{3}}),\sin(\omega t-{\frac {4\pi }{3}})]'$ .

Ainsi la modulante à comparer avec la porteuse triangulaire (entre 0 et 1) devient :

$V_{mod}={\frac {\mathbf {U} _{ref}}{V_{DC}}}+v_{0}+{\frac {1}{2}}={\frac {\mathbf {U} _{ref}}{V_{DC}}}-{\frac {\max(\mathbf {U} _{ref})+\min(\mathbf {U} _{ref})}{2V_{DC}}}+{\frac {1}{2}}$ .

Les notations utilisées sont les suivantes :

$V_{DC}$ Tension de Bus.
$v_{0}$ Tension de mode commun.
$m={\frac {V_{1}}{V_{DC}}}$ indice de modulation (avec $V_{1}$ l'amplitude du fondamental).
$\omega$ pulsation de référence.

Tension de consigne

La méthode a besoin d'une tension de référence échantillonnée à une fréquence f_s (T_s = 1/f_s). L'utilisation de la transformée de Clarke permet d'obtenir une tension de référence unique à partir d'un système triphasé.

Vecteur spatial 3D

Une méthode du vecteur spatial en 3D existe également. Elle permet de commander les onduleurs à quatre branches. Le vecteur n'est plus représenté dans un hexagone mais dans un prisme en trois dimensions, comme un prisme hexagonal si on utilise la transformée de Clarke^[6] ou un dodécaèdre sinon^[7].

Autres modulations vectorielles

Il existe de nombreuses méthodes de commandes vectorielles, dont le principal usage est de réduire la tension de mode commun (common voltage mode, CMV en anglais) afin de réduire les problèmes liés à la compatibilité électromagnétique. L'ensemble des modulations vectorielles qui réduisent le CMV n'utilisent pas les vecteurs 0 et 7 (respectivement 000 et 111 dans un onduleur trois bras deux niveaux). Cependant, la contrepartie de ce mode de stratégie est de limiter l'ensemble des tensions accessibles en rendant infaisable la réalisation de certains vecteurs de tension.

MLI "à distance"

Les MLI dites à distance ou (Remote state PWM, RSPWM en anglais) sont des stratégies qui ne vont utiliser que 3 vecteurs déphasés chacun de ${\frac {2\pi }{3}}$ rad entre eux. De cette manière la tension de mode commun est égale à $\pm {\frac {V_{DC}}{6}}$ . Il existe trois grandes classes de PWM, la RSPWM1 (utilisant les vecteurs 1,3 et 5), la RSPWM2 (vecteurs 2,4 et 6) et la RSPWM3 oscillant entre les deux autres stratégies^[8]^,^[9].

MLI à séquence nulle de tension active

Les MLI à séquence nulle de tension active (Acrive zero sequence component PWM, AZSPWM en anglais) sont des techniques qui elles aussi diminuent la CMV. Pour ce faire, on va remplacer la séquence nulle de tension réalisée avec les vecteurs 0 et 7 dans la MLI vectorielle traditionnelle, par l'usage de deux vecteurs complémentaires. Par exemple, dans le premier secteur, la SVM utilise les vecteurs 1 et 2 pour réaliser la tension, ainsi ces deux vecteurs doivent aussi être présents dans la stratégie AZSPWM. Il reste ainsi les vecteurs 3 et 6 pour réaliser la séquence nulle de tension. En faisant s'enchainer les vecteurs de la façon suivante: $\mathbf {U} _{6}\mathbf {U} _{1}\mathbf {U} _{2}\mathbf {U} _{3}\mathbf {U} _{3}\mathbf {U} _{2}\mathbf {U} _{1}\mathbf {U} _{6}$ . Dans ce cas les vecteurs restent adjacents, c'est ce qu'on appelle la AZSPWM1. Si l'adjacence n'est plus respectée, c'est ce que l'on appelle la AZSPWM2 (dans le cas du premier secteur: $\mathbf {U} _{3}\mathbf {U} _{1}\mathbf {U} _{2}\mathbf {U} _{6}\mathbf {U} _{6}\mathbf {U} _{2}\mathbf {U} _{1}\mathbf {U} _{3}$ ). Enfin la AZSPWM3 va se servir d'un vecteur déjà utilisé (dans le premier secteur le 1), va rallonger sa durée d'utilisation et utiliser son vecteur complémentaire. Dans le cas du premier secteur, la séquence donne: $\mathbf {U} _{1}\mathbf {U} _{1}\mathbf {U} _{2}\mathbf {U} _{4}\mathbf {U} _{4}\mathbf {U} _{2}\mathbf {U} _{1}\mathbf {U} _{1}$ ^[10]^,^[8].

MLI dite d'état proche

La MLI dite d'état proche ou (Near State PWM, NSPWM en anglais) est une technique de MLI qui consiste à prendre les 3 vecteurs adjacents au secteur courant. Il est à noter que désormais les secteurs sont dans ce cas précis centrés autour d'un vecteur réalisable par l'onduleur et non entre deux vecteurs. Ainsi la définition des secteurs est déphasée de 30°. Cette technique permet de se passer des vecteurs nuls (0 ou 7) et ainsi réduit considérablement la CMV. Le principal défaut de cette méthode est que les indices de modulation faibles ne sont pas réalisables^[11].

La commande Delta-Sigma

La commande Delta-Sigma ou $\Delta \Sigma$ est une méthode de régulation vectorielle de tension en boucle fermée (contrairement à beaucoup d'autres). La différence entre le vecteur de sortie et le vecteur de référence est d'abord réalisée, il s'agit du calcul de $\Delta$ , ensuite, cette différence est intégrée pour donner l'accumulation de l'erreur $\Sigma$ qui grâce à un algorithme va permettre de suivre la référence. Si $\Sigma$ est plus grand qu'une certaine erreur $S$ le vecteur actuel de tension appliqué va changer, dans le cas contraire, on garde le vecteur qui était appliqué. La détermination du nouveau vecteur se fait grâce à un calcul qui permet de décider quel vecteur va permettre de rentrer dans le cercle de rayon $S$ et ce de manière la plus durable ^[12]^,^[13].

Applications

La méthode est utilisée pour commander les onduleurs connectés à des machines électriques asynchrones, synchrones ou à courant continu sans balais. Elle est souvent utilisée en combinaison avec une commande vectorielle pour produire la consigne de tension.

Notes et références

(de) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en allemand intitulé « Raumzeigermodulation » (voir la liste des auteurs).

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Space vector modulation » (voir la liste des auteurs).

↑ ^{a b et c} (en) Holmes, Pulse width modulation for power converters : Principles and practice, John Wiley & Sons, 2003.
↑ ^{a b c d et e} « Les Différents Stratégies de Modulation » (consulté le 20 mai 2015)
↑ (en) Emre Ün et Ahmet M. Hava, « A Near-State PWM Method With Reduced Switching Losses and Reduced Common-Mode Voltage for Three-Phase Voltage Source Inverters », IEEE Transactions on Industry Applications, vol. 45, n^o 2,‎ 2009, p. 782-793 (lire en ligne, consulté le 8 mars 2022).
↑ (en) Holmes, « The general relationship between regular-sampled pulse-width-modulation and space vector modulation for hard switched converters », Conference Record of the 1992 IEEE Industry Applications Society Annual Meeting, vol. 1,‎ 1992, p. 1002-1009 (DOI 10.1109/IAS.1992.244437).
↑ (en) Zhou, « Relationship between space-vector modulation and threephase carrier-based pwm: a comprehensive analysis [three-phase inverters] », IEEE Transactions on Industrial Electronics, vol. 49, n^o 1,‎ 2002, p. 186-196 (DOI 10.1109/41.982262).
↑ (en) R. Zhang, V. Himamshu Prasad, D. Boroyevich et F.C. Lee, « Three-Dimensional Space Vector Modulation for Four-Leg Voltage-Source Converters », IEEE Power Electronics Letters, vol. 17, n^o 3,‎ mai 2002
↑ (en) M.A. Perales, M.M. Prats, R. Portillo, J.L. Mora, J.I. León et L.G. Franquelo, « Three-Dimensional Space Vector Modulation in abc Coordinates for Four-Leg Voltage Source Converters », IEEE Power Electronics Letters, vol. 1, n^o 4,‎ décembre 2003
↑ ^{a et b} (en) Hava, « Performance analysis of reduced common-mode voltage pwm methods and comparison with standard pwm methods for three-phase voltagesource inverters », IEEE Transactions on Power Electronics, vol. 24, n^o 1,‎ 2009, p. 241-252 (DOI 10.1109/TPEL.2008.2005719).
↑ (en) Baik, « Remote-state pwm with minimum rms torque ripple and reduced common-mode voltage for three-phase vsi-fed blac motor drives », Electronics, vol. 9, n^o 4,‎ 2020, p. 586.
↑ (en) Son, « A new active common-mode emi filter for pwm inverter », IEEE Transactions on Power Electronics, vol. 18, n^o 6,‎ 2003, p. 1309-1314 (DOI 10.1109/TPEL.2003.818829).
↑ (en) Ün, « A near-state pwm method with reduced switching losses and reduced common-mode voltage for three-phase voltage source inverters », IEEE Transactions on Industry Applications, vol. 45, n^o 2,‎ 2009, p. 782-793 (DOI 10.1109/TIA.2009.2013580.).
↑ (en) Friedrich, « A comparison between two pwm strategics: natural sampling and instantaneous feedback », EPE 1986,‎ 1987, p. 281-285.
↑ Vilain, « Une nouvelle stratégie de modulation du vecteur d’espace pour un onduleur de tension triphasé: la modulation delta sigma vectorielle », Journal de Physique III, vol. 5, n^o 7,‎ 1995, p. 1075-1088.

Bibliographie

(de) Dierk Schröder, Elektrische Antriebe : Grundlagen, Berlin, Heidelberg, Springer, 2009 (ISBN 978-3-642-02989-9)
(de) Dierk Schröder, Antriebe : Regelung von Antriebssystemen, Berlin, Heidelberg, Springer, 2009, 1336 p. (ISBN 978-3-540-89612-8)

Portail de l’électricité et de l’électronique

[Holmes2003-1] {a b et c} (en) Holmes, Pulse width modulation for power converters : Principles and practice, John Wiley & Sons, 2003.

[master-2] {a b c d et e} « Les Différents Stratégies de Modulation » (consulté le 20 mai 2015)

[3] (en) Emre Ün et Ahmet M. Hava, « A Near-State PWM Method With Reduced Switching Losses and Reduced Common-Mode Voltage for Three-Phase Voltage Source Inverters », IEEE Transactions on Industry Applications, vol. 45, n^o 2,‎ 2009, p. 782-793 (lire en ligne, consulté le 8 mars 2022).

[4] (en) Holmes, « The general relationship between regular-sampled pulse-width-modulation and space vector modulation for hard switched converters », Conference Record of the 1992 IEEE Industry Applications Society Annual Meeting, vol. 1,‎ 1992, p. 1002-1009 (DOI 10.1109/IAS.1992.244437).

[5] (en) Zhou, « Relationship between space-vector modulation and threephase carrier-based pwm: a comprehensive analysis [three-phase inverters] », IEEE Transactions on Industrial Electronics, vol. 49, n^o 1,‎ 2002, p. 186-196 (DOI 10.1109/41.982262).

[6] (en) R. Zhang, V. Himamshu Prasad, D. Boroyevich et F.C. Lee, « Three-Dimensional Space Vector Modulation for Four-Leg Voltage-Source Converters », IEEE Power Electronics Letters, vol. 17, n^o 3,‎ mai 2002

[7] (en) M.A. Perales, M.M. Prats, R. Portillo, J.L. Mora, J.I. León et L.G. Franquelo, « Three-Dimensional Space Vector Modulation in abc Coordinates for Four-Leg Voltage Source Converters », IEEE Power Electronics Letters, vol. 1, n^o 4,‎ décembre 2003

[Hava2009-8] {a et b} (en) Hava, « Performance analysis of reduced common-mode voltage pwm methods and comparison with standard pwm methods for three-phase voltagesource inverters », IEEE Transactions on Power Electronics, vol. 24, n^o 1,‎ 2009, p. 241-252 (DOI 10.1109/TPEL.2008.2005719).

[9] (en) Baik, « Remote-state pwm with minimum rms torque ripple and reduced common-mode voltage for three-phase vsi-fed blac motor drives », Electronics, vol. 9, n^o 4,‎ 2020, p. 586.

[10] (en) Son, « A new active common-mode emi filter for pwm inverter », IEEE Transactions on Power Electronics, vol. 18, n^o 6,‎ 2003, p. 1309-1314 (DOI 10.1109/TPEL.2003.818829).

[11] (en) Ün, « A near-state pwm method with reduced switching losses and reduced common-mode voltage for three-phase voltage source inverters », IEEE Transactions on Industry Applications, vol. 45, n^o 2,‎ 2009, p. 782-793 (DOI 10.1109/TIA.2009.2013580.).

[12] (en) Friedrich, « A comparison between two pwm strategics: natural sampling and instantaneous feedback », EPE 1986,‎ 1987, p. 281-285.

[13] Vilain, « Une nouvelle stratégie de modulation du vecteur d’espace pour un onduleur de tension triphasé: la modulation delta sigma vectorielle », Journal de Physique III, vol. 5, n^o 7,‎ 1995, p. 1075-1088.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]