Loi parabolique

En théorie des probabilités et en statistique, la loi parabolique est une loi de probabilité continue dont la densité de probabilité est définie à partir d'une fonction polynomiale de degré deux, c'est-à-dire une fonction $f(x)=\alpha \left(x-\beta \right)^{2}$ qui dépend de deux paramètres.

Loi parabolique
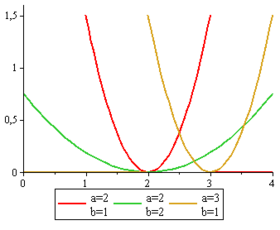Densité de probabilité
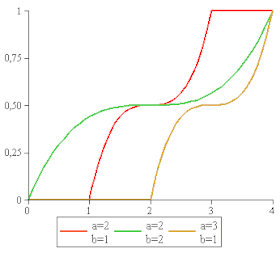Fonction de répartition
Paramètres	$a\in ]-\infty ,\infty [$ $b>0$ ou $\alpha >0$ $\beta \in ]-\infty ,\infty [,$
Support	$x\in [a-b,a+b]\!$
Densité de probabilité	$\alpha \left(x-\beta \right)^{2}$
Fonction de répartition	${\alpha \over 3}\left((x-\beta )^{3}-{\frac {3}{2\alpha }}\right)$
Espérance	$a=\beta$
Médiane	$a=\beta$
Variance	${3 \over 5}b^{2}$
Asymétrie	$0$
Kurtosis normalisé	$-{\frac {38}{21}}$

Cette loi est également appelée loi parabolique de forme $\cup$. De manière similaire on peut définir la loi parabolique de forme $\cap$.

Densité de probabilité

La densité de probabilité de la loi parabolique est :

$f(x)={\begin{cases}\alpha \left(x-\beta \right)^{2}&{\hbox{ pour }}x\in [\beta -({\frac {3}{2\alpha }})^{1/3},\beta +({\frac {3}{2\alpha }})^{1/3}]\\0&{\hbox{ sinon.}}\end{cases}}$

où $\alpha >0$, $\beta \in \mathbb {R}$.

Il est parfois plus simple de considérer la fonction de densité sous une forme différente :

$f(x)={\begin{cases}{\frac {3}{2b}}\left({\frac {x-a}{b}}\right)^{2}&{\hbox{ pour }}x\in [a-b,a+b]\\0&{\hbox{ sinon.}}\end{cases}}$

où $a\in \mathbb {R}$, $b>0$.

Les coefficients $a=\beta$ représentent la moyenne de la loi. Les coefficients $\alpha ={\frac {3}{2b^{3}}}$ donnent l'échelle verticale de la parabole.

Fonction de répartition

La fonction de répartition de la loi parabolique est :

$F(x)={\begin{cases}0&{\hbox{ pour }}x<\beta -({\frac {3}{2\alpha }})^{1/3}\\\displaystyle {\alpha \over 3}\left((x-\beta )^{3}-{\frac {3}{2\alpha }}\right)&{\hbox{ pour }}x\in [\beta -({\frac {3}{2\alpha }})^{1/3},\beta +({\frac {3}{2\alpha }})^{1/3}]\\1&{\hbox{ pour }}x>\beta +({\frac {3}{2\alpha }})^{1/3}\end{cases}}$

ou

$F(x)={\begin{cases}0&{\hbox{ pour }}x<a-b\\{\frac {1}{2}}\left[\left({\frac {x-a}{b}}\right)^{3}+1\right]&{\hbox{ pour }}x\in [a-b,a+b]\\1&{\hbox{ pour }}x>b+a\end{cases}}$

Applications

Cette loi est un modèle utile pour des processus symétriques. D'autres lois continues permettent plus de flexibilité en termes de relâchement de symétrie et de forme parabolique de la densité, comme la loi bêta, la loi Gamma…

Références

• Horst Rinne, « (en) Location–Scale Distributions - Linear Estimation and Probability Plotting Using MATLAB », 2010 (consulté le 7 mars 12), p. 167