Loi normale asymétrique

En théorie des probabilités et en statistiques, la distribution normale asymétrique est une loi de probabilité continue qui généralise la distribution normale en introduisant une asymétrie non nulle.

Distribution normale asymétrique
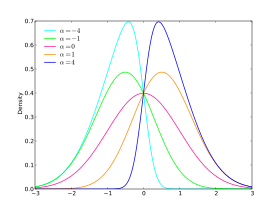Densité de probabilité
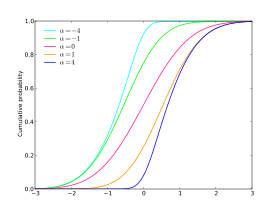Fonction de répartition
Paramètres	$\xi \,$ position (réel) $\omega \,$ échelle (réel positif) $\alpha \,$ forme (asymétrie) (réel)
Support	$x\in (-\infty ;+\infty )\!$
Densité de probabilité	${\frac {1}{\omega \pi }}e^{-{\frac {(x-\xi )^{2}}{2\omega ^{2}}}}\int _{-\infty }^{\alpha \left({\frac {x-\xi }{\omega }}\right)}e^{-{\frac {t^{2}}{2}}}\ dt$
Fonction de répartition	$\Phi \left({\frac {x-\xi }{\omega }}\right)-2T\left({\frac {x-\xi }{\omega }},\alpha \right)$ $T(h,a)$ est la fonction T d'Owen
Espérance	$\xi +\omega \delta {\sqrt {\frac {2}{\pi }}}$ où $\delta ={\frac {\alpha }{\sqrt {1+\alpha ^{2}}}}$
Variance	$\omega ^{2}\left(1-{\frac {2\delta ^{2}}{\pi }}\right)$
Asymétrie	${\frac {4-\pi }{2}}{\frac {\left(\delta {\sqrt {2/\pi }}\right)^{3}}{\left(1-2\delta ^{2}/\pi \right)^{3/2}}}$
Kurtosis normalisé	$2(\pi -3){\frac {\left(\delta {\sqrt {2/\pi }}\right)^{4}}{\left(1-2\delta ^{2}/\pi \right)^{2}}}$
Fonction génératrice des moments	$2\exp \left(\mu \,t+\sigma ^{2}{\frac {t^{2}}{2}}\right)\Phi (\sigma \delta t)$
Fonction caractéristique	$\exp \left(\mu \,i\,t-{\frac {\sigma ^{2}t^{2}}{2}}\right)\left(1+i\,\operatorname {erf} \left({\frac {\sigma \delta t}{\sqrt {2}}}\right)\right)$

Définition

Soit $\phi (x)$ la densité de probabilité de la loi normale centrée réduite

$\phi (x)={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {x^{2}}{2}}}$

avec sa fonction de répartition donnée par

$\Phi (x)=\int _{-\infty }^{x}\phi (t)\ dt={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)\right]$

avec erf la fonction d'erreur.

Alors la densité de probabilité de la distribution normale asymétrique de paramètre α est donnée par

$f(x)=2\phi (x)\Phi (\alpha x).\,$

Pour ajouter un paramètre de position et un paramètre d'échelle à cela, on utilise la transformation usuelle $x\mapsto {\frac {x-\xi }{\omega }}$. On peut vérifier que l'on retrouve une distribution normale lorsque $\alpha =0$, et que la valeur absolue de l'asymétrie augmente lorsque la valeur absolue de $\alpha$ augmente. La distribution est asymétrique vers la droite si $\alpha >0$ et est asymétrique vers la gauche si $\alpha <0$. La densité de probabilité avec un paramètre de position ξ, un paramètre d'échelle ω, et un paramètre d'asymétrie α devient

$f(x)={\frac {2}{\omega }}\phi \left({\frac {x-\xi }{\omega }}\right)\Phi \left(\alpha \left({\frac {x-\xi }{\omega }}\right)\right).\,$

Estimation

L'estimateur du maximum de vraisemblance pour $\xi$, $\omega$, et $\alpha$ peut être calculé numériquement, mais il n'existe pas d'expression directe des estimateurs sauf si $\alpha =0$. Si l'on a besoin d'une expression explicite, la méthode des moments peut être appliquée pour estimer $\alpha$ à partir de l'asymétrie empirique de l'échantillon, en inversant l'équation d'asymétrie. Cela donne l'estimateur

$|\delta |={\sqrt {{\frac {\pi }{2}}{\frac {|{\hat {\gamma }}_{3}|^{\frac {2}{3}}}{|{\hat {\gamma }}_{3}|^{\frac {2}{3}}+((4-\pi )/2)^{\frac {2}{3}}}}}}$

où $\delta ={\frac {\alpha }{\sqrt {1+\alpha ^{2}}}}$, et ${\hat {\gamma }}_{3}$ est l'asymétrie empirique. Le signe de $\delta$ est le même que celui de ${\hat {\gamma }}_{3}$. Par conséquent, ${\hat {\alpha }}=\delta /{\sqrt {1-\delta ^{2}}}$.

Référence

(en) A. Azzalini, « A class of distributions which includes the normal ones », Scand. J. Statist., vol. 12,‎ 1985, p. 171–178

Article connexe

Asymétrie (statistique)

Liens externes

• A very brief introduction to the skew-normal distribution
• The Skew-Normal Probability Distribution (and related distributions, such as the skew-t)
• OWENS: Owen's T Function
• Closed-skew Distributions - Simulation, Inversion and Parameter Estimation