Loi logit-normale

En théorie des probabilités et en statistique, la loi logit-normale est une loi de probabilité telle que la fonction logit de cette loi soit de loi normale. Si Y est une variable aléatoire de loi normale, et P est la fonction logistique, alors $X=P(Y)$ est de loi logit-normale, de manière similaire, si X est de loi logit-normale, alors $Y=logit(X)$ est de loi normale.

Logit-normal
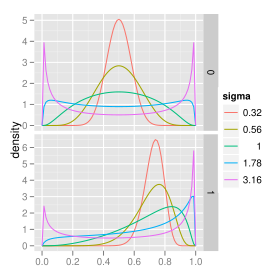Densité de probabilité
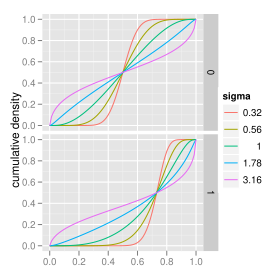Fonction de répartition
Paramètres	σ2 > 0, $\mu \in \mathbb {R}$
Support	$x\in ]0,1[$
Densité de probabilité	${\frac {1}{\sigma {\sqrt {2\pi }}}}\,e^{-{\frac {(\operatorname {logit} (x)-\mu )^{2}}{2\sigma ^{2}}}}{\frac {1}{x(1-x)}}$
Fonction de répartition	${\frac {1}{2}}{\Big [}1+\operatorname {erf} {\Big (}{\frac {\operatorname {logit} (x)-\mu }{\sqrt {2\sigma ^{2}}}}{\Big )}{\Big ]}$
Espérance	pas d'expression analytique
Médiane	$P(\mu )\,$
Mode	pas d'expression analytique
Variance	pas d'expression analytique
Fonction génératrice des moments	pas d'expression analytique

Caractérisations

densité de probabilité

La densité de probabilité de la loi logit-normale est :

$f_{X}(x;\mu ,\sigma )={\begin{cases}\displaystyle {\frac {1}{\sigma {\sqrt {2\pi }}}}\,e^{-{\frac {(\operatorname {logit} (x)-\mu )^{2}}{2\sigma ^{2}}}}{\frac {1}{x(1-x)}}&{\hbox{ pour }}x\in ]0,1[\\0&{\hbox{ sinon }}\end{cases}}$

où μ et σ sont l'espérance et l'écart-type du logit de la variable (par définition, le logit de X est de loi normale).

La densité obtenue en changeant le signe de μ est symétrique, c'est-à-dire $f_{X}(x;\mu ,\sigma )=f_{X}(1-x;-\mu ,\sigma )$, le nouveau mode est symétrique à l'ancien par rapport à 1/2.

Moments

Les moments de la loi logit-normale n'ont pas d'expression analytique. Il est cependant possible de les estimer par des approximations d'intégrales.

Notes et références

• Frederic, P. & Lad, F. (2008) Two Moments of the Logitnormal Distribution. Communications in Statistics-Simulation and Computation. 37: 1263-1269
• Mead, « A Generalised Logit-Normal Distribution », Biometrics, vol. 21, n^o 3,‎ 1965, p. 721–732 (DOI 10.2307/2528553, JSTOR 2528553)

Voir aussi

Articles connexes

• loi normale.
• loi bêta et loi Kumaraswamy qui sont des lois à deux paramètres ayant la même forme.

Liens externes

• logitnorm package pour R.