Loi logistique

En probabilité et en statistiques, la loi logistique est une loi de probabilité absolument continue à support infini utilisé en régression logistique et pour les réseaux de neurones à propagation avant. Son nom de loi logistique est issu du fait que sa fonction de répartition est une fonction logistique.

Loi logistique
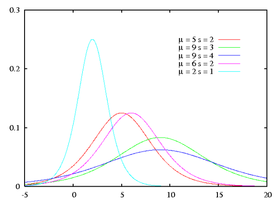
Densité de probabilité
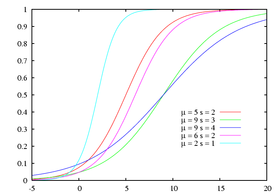
Fonction de répartition
Paramètres	$\mu \,$ réel $s>0\,$ réel
Support	$x\in ]-\infty ,+\infty [$
Densité de probabilité	${\frac {{\rm {e}}^{-(x-\mu )/s}}{s\left(1+{\rm {e}}^{-(x-\mu )/s}\right)^{2}}}\!$
Fonction de répartition	${\frac {1}{1+{\rm {e}}^{-(x-\mu )/s}}}\!$
Espérance	$\mu \,$
Médiane	$\mu \,$
Mode	$\mu \,$
Variance	${\frac {\pi ^{2}}{3}}s^{2}\!$
Asymétrie	$0\,$
Kurtosis normalisé	$6/5\,$
Entropie	$\ln(s)+2\,$
Fonction génératrice des moments	${\rm {e}}^{\mu \,t}\,\mathrm {B} (1-s\,t,\;1+s\,t)\!$ pour $|s\,t|<1\!$, Fonction bêta
Fonction caractéristique	${\rm {e}}^{{\rm {i}}\mu t}\,\mathrm {B} (1-ist,\;1+ist)\,$ pour $|{\rm {i}}st|<1\,$

Définition et propriétés

La loi logistique a deux paramètres μ et s > 0 et sa densité est

$f(x;\mu ,{s})={\frac {{\rm {e}}^{-{\frac {x-\mu }{s}}}}{s\left(1+{\rm {e}}^{-{\frac {x-\mu }{s}}}\right)^{2}}}={\frac {1}{4s}}\operatorname {sech} ^{2}\!\left({\frac {x-\mu }{2s}}\right)$

Sa fonction de répartition est

$F(x;\mu ,s)={\frac {1}{1+{\rm {e}}^{-{\frac {x-\mu }{s}}}}}={\frac {1}{2}}+{\frac {1}{2}}\;\operatorname {tanh} \!\left({\frac {x-\mu }{2s}}\right).$

Son espérance et sa variance sont données par les formules suivantes :

$\mathbb {E} (X)=\mu \,$

${\textrm {Var}}(X)={\frac {s^{2}\pi ^{2}}{3}}$

La loi logistique standard est la loi logistique de paramètres 0 et 1. Sa fonction de répartition est la sigmoïde :

$F(x)={\frac {1}{1+{\rm {e}}^{-x}}}$

Son espérance vaut alors 0 et sa variance π²/3.

Distributions associées

• Si $X\sim {\textrm {logistique}}(\mu ,\beta )$ alors $kX+l\sim {\textrm {logistique}}(k\mu +l,k\beta )$.
• Si $X\sim {\mathcal {U}}(0;1)$ (loi uniforme continue) alors $\mu +\beta (\ln(X)-\ln(1-X))\sim {\textrm {logistique}}(\mu ,\beta )$
• Si $X,Y\sim {\mathcal {G}}(\alpha ,\beta )$ (loi de Gumbel) alors $X-Y\sim {\textrm {logistique}}(0,\beta )$.
• Si $X,Y\sim {\mathcal {GEV}}(\alpha ,\beta ,0)$ (loi d'extremum généralisée) alors $X-Y\sim {\textrm {logistique}}(0,\beta )$.
• Si $X\sim {\mathcal {G}}(\alpha ,\beta ),\,Y\sim {\mathcal {GEV}}(\alpha ,\beta ,0)$ alors $X+Y\sim {\textrm {logistique}}(2\alpha ,\beta )$.
• Si $X\sim {\textrm {logistique}}(\mu ,s)$ alors son exponentielle suit une loi log-logistique : $\exp(X)\sim \log -{\textrm {logistique}}\left(\alpha ={\rm {e}}^{\mu },\beta ={\frac {1}{s}}\right)$, et $\exp(X)+\gamma \sim \log -{\textrm {logistique}}3\left(\alpha ={\rm {e}}^{\mu },\beta ={\frac {1}{s}},\gamma \right)$ (loi log-logistique à trois paramètres)
• Si $X\sim {\mathcal {E}}(1)$ (loi exponentielle) alors

$\mu +\beta \ln({\rm {e}}^{X}-1)\sim \operatorname {logistique} (\mu ,\beta ).$

• Si $X,Y\sim {\mathcal {E}}(1)$alors

$\mu -\beta \ln \left({\frac {X}{Y}}\right)\sim \operatorname {logistique} (\mu ,\beta ).$

Utilisations

La loi logistique est aussi utilisée pour le classement Elo.

Voir aussi

• Fonction logistique
• Régression logistique
• Logit
• Loi log-logistique
• Loi sécante hyperbolique
• Sigmoïde (mathématiques)

Liens externes

• (en) Eric W. Weisstein, « Logistic Distribution », sur MathWorld