Loi inverse-χ²

En théorie des probabilités et en statistique, la loi inverse-$\chi ^{2}$ (ou loi du $\chi ^{2}$ inverse) est la loi de probabilité de la variable aléatoire dont l'inverse suit une loi du χ². Une variante par changement d'échelle existe également.

Loi inverse-χ2
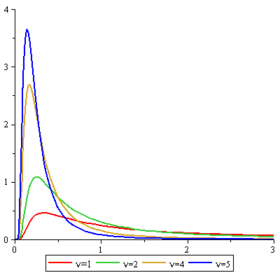Densité de probabilité
Fonction de répartition
Paramètres	$\nu >0\!$
Support	$x\in ]0,\infty [\!$
Densité de probabilité	${\frac {2^{-\nu /2}}{\Gamma (\nu /2)}}\,x^{-\nu /2-1}e^{-1/(2x)}\!$
Fonction de répartition	$\Gamma \!\left({\frac {\nu }{2}},{\frac {1}{2x}}\right){\bigg /}\,\Gamma \!\left({\frac {\nu }{2}}\right)\!$
Espérance	${\frac {1}{\nu -2}}\!$ pour $\nu >2\!$
Mode	${\frac {1}{\nu +2}}\!$
Variance	${\frac {2}{(\nu -2)^{2}(\nu -4)}}\!$ pour $\nu >4\!$
Asymétrie	${\frac {4}{\nu -6}}{\sqrt {2(\nu -4)}}\!$ pour $\nu >6\!$
Kurtosis normalisé	${\frac {12(5\nu -22)}{(\nu -6)(\nu -8)}}\!$ pour $\nu >8\!$
Entropie	$\scriptstyle {\frac {\nu }{2}}+\ln \left({\frac {1}{2}}\Gamma \!\left({\frac {\nu }{2}}\right)\right)-\left(1+{\frac {\nu }{2}}\right)\psi \left({\frac {\nu }{2}}\right)$
Fonction génératrice des moments	${\frac {2}{\Gamma ({\frac {\nu }{2}})}}\left({\frac {-t}{2\mathrm {i} }}\right)^{\!\!{\frac {\nu }{4}}}K_{\frac {\nu }{2}}\!\left({\sqrt {-2t}}\right)$
Fonction caractéristique	${\frac {2}{\Gamma ({\frac {\nu }{2}})}}\left({\frac {-\mathrm {i} t}{2}}\right)^{\!\!{\frac {\nu }{4}}}K_{\frac {\nu }{2}}\!\left({\sqrt {-2\mathrm {i} t}}\right)$

Cette loi est utilisée en inférence statistique. Si X suit une loi inverse-χ², on notera : $X\sim {\mbox{Inv-}}\chi ^{2}(\nu )$.

Définition

Si X suit une loi du χ² à $\nu$ degrés de liberté, alors $1/X$ est de loi inverse-χ² à $\nu$ degrés de liberté.

Sa densité de probabilité est donnée par :

$f(x;\nu )={\begin{cases}\displaystyle {\frac {2^{-\nu /2}}{\Gamma (\nu /2)}}\,x^{-\nu /2-1}\mathrm {e} ^{-1/(2x)}&{\text{ si }}x>0\\0&{\text{ sinon}}\end{cases}}$

où $\Gamma$ est la fonction gamma et $\nu$ est appelé le nombre de degrés de liberté.

Variante

Une variante de la loi inverse-χ² existe, par un changement d'échelle. C'est la loi de $\nu /X$ lorsque X suit une loi du χ² à $\nu$ degrés de liberté. La densité de probabilité est alors donnée par :

$f(x;\nu )={\begin{cases}\displaystyle {\frac {(\nu /2)^{\nu /2}}{\Gamma (\nu /2)}}x^{-\nu /2-1}\mathrm {e} ^{-\nu /(2x)}&{\text{ si }}x>0\\0&{\text{ sinon.}}\end{cases}}$

Le degré de liberté est encore $\nu$.

Liens avec d'autres lois

• loi du χ² : Si $X\thicksim \chi ^{2}(\nu )$, alors ${\frac {1}{X}}\thicksim {\mbox{Inv-}}\chi ^{2}(\nu )$.
• la loi inverse-χ² est la loi inverse-gamma avec $\alpha ={\frac {\nu }{2}}$ et $\beta ={\frac {1}{2}}$.

Voir aussi

Liens externes

• (en) Eric W. Weisstein, « Inverse Chi-Squared Distribution », sur MathWorld
• InvChisquare dans le paquet geoR pour le langage R.