Interpolation bicubique

En mathématiques, l'interpolation bicubique est une extension de l'interpolation cubique pour interpoler un ensemble de points distribués sur une grille régulière bidimensionnelle. La surface interpolée est plus lisse que les surfaces correspondantes obtenues par interpolation bilinéaire ou par sélection du plus proche voisin. L'interpolation bicubique peut être accomplie en utilisant soit des polynômes de Lagrange, soit des splines cubiques, soit un algorithme de convolution cubique.

Illustration de l'interpolation bicubique sur un ensemble de données aléatoires

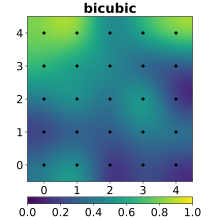
Dans le domaine du traitement d'images numériques, l'interpolation bicubique est souvent préférée à une interpolation bilinéaire ou à la technique du plus proche voisin pour le ré-échantillonnage d'images, lorsque le temps de traitement n'est pas critique. Contrairement à une interpolation bilinéaire, qui ne prend que 4 pixels (2 × 2) en compte, l'interpolation bicubique considère un voisinage de 16 pixels (4 × 4). Les images ré-échantillonnées par une interpolation bicubique sont donc plus lisses et ont moins d'artefacts d'interpolation.

Développement

Supposons que les valeurs de la fonction $f$ et les dérivés $f_{x}$, $f_{y}$ et $f_{xy}$ sont connues aux quatre coins $(0,0),(1,0),(0,1)$ et $(1,1)$ d'un carré unitaire. La surface interpolée peut alors être écrite :

$p(x,y)=\sum _{i=0}^{3}\sum _{j=0}^{3}a_{ij}x^{i}y^{j}.$

Le problème de l'interpolation consiste à déterminer les seize coefficients $a_{ij}$. La fonction $f$ évaluée en ces quatre points, nous donne ces quatre équations :

1. $f(0,0)=p(0,0)=a_{00}$
2. $f(1,0)=p(1,0)=a_{00}+a_{10}+a_{20}+a_{30}$
3. $f(0,1)=p(0,1)=a_{00}+a_{01}+a_{02}+a_{03}$
4. $f(1,1)=p(1,1)=\textstyle \sum _{i=0}^{3}\sum _{j=0}^{3}a_{ij}$

De même, en évaluant les dérivées partielles $f_{x}$ et $f_{y}$ à ces quatre points, on obtient les huit équations :

1. $f_{x}(0,0)=p_{x}(0,0)=a_{10}$
2. $f_{x}(1,0)=p_{x}(1,0)=a_{10}+2a_{20}+3a_{30}$
3. $f_{x}(0,1)=p_{x}(0,1)=a_{10}+a_{11}+a_{12}+a_{13}$
4. $f_{x}(1,1)=p_{x}(1,1)=\textstyle \sum _{i=1}^{3}\sum _{j=0}^{3}a_{ij}i$
5. $f_{y}(0,0)=p_{y}(0,0)=a_{01}$
6. $f_{y}(1,0)=p_{y}(1,0)=a_{01}+a_{11}+a_{21}+a_{31}$
7. $f_{y}(0,1)=p_{y}(0,1)=a_{01}+2a_{02}+3a_{03}$
8. $f_{y}(1,1)=p_{y}(1,1)=\textstyle \sum _{i=0}^{3}\sum _{j=1}^{3}a_{ij}j$

Finalement, les quatre équations suivantes sont obtenues en évaluant la dérivée partielle $f_{xy}$

1. $f_{xy}(0,0)=p_{xy}(0,0)=a_{11}$
2. $f_{xy}(1,0)=p_{xy}(1,0)=a_{11}+2a_{21}+3a_{31}$
3. $f_{xy}(0,1)=p_{xy}(0,1)=a_{11}+2a_{12}+3a_{13}$
4. $f_{xy}(1,1)=p_{xy}(1,1)=\textstyle \sum _{i=1}^{3}\sum _{j=1}^{3}a_{ij}ij$

Dans les expressions ci-dessus,

$p_{x}(x,y)=\textstyle \sum _{i=1}^{3}\sum _{j=0}^{3}a_{ij}ix^{i-1}y^{j}$

$p_{y}(x,y)=\textstyle \sum _{i=0}^{3}\sum _{j=1}^{3}a_{ij}x^{i}jy^{j-1}$

$p_{xy}(x,y)=\textstyle \sum _{i=1}^{3}\sum _{j=1}^{3}a_{ij}ix^{i-1}jy^{j-1}$.

Cette procédure donne une surface $p(x,y)$ sur le carré unitaire $[0,1]\times [0,1]$ qui est continue et a des dérivées continues. L'interpolation bicubique sur une grille régulière de taille quelconque peut donc être réalisée en recollant des surfaces unitaires interpolées bicubiques, en s'assurant que les dérivées aux limites correspondent.

Trouver les dérivées à partir des valeurs de la fonction

Si les dérivées sont inconnues, elles sont généralement estimées à partir des valeurs de la fonction au voisinage des coins du carré unitaire à interpoler, par exemple en utilisant les différences finies.

Pour trouver l'une des dérivées simples, $f_{x}$ ou $f_{y}$, en utilisant cette méthode, trouver la pente entre les deux points environnants selon l'axe approprié. Par exemple, pour calculer $f_{x}$ pour un point cible, trouver $f(x,y)$ pour les points à gauche et à droite du point cible et calculer la pente. De même pour calculer $f_{y}$ en un point cible, il faut calculer $f(x,y)$ pour les points au-dessus et en-dessous du point cible, et calculer la pente.

Pour trouver la dérivée croisée, $f_{xy}$, prendre les dérivées selon les deux axes, une par une. Par exemple, on peut utiliser d'abord la procédure pour calculer $f_{x}$, la dérivée selon $X$, pour les points au-dessus et en dessous du point cible, et ensuite utiliser la procédure pour calculer $f_{y}$, la dérivée selon $Y$, sur ces dérivées selon $X$ (plutôt que de calculer $f_{y}$ sur les valeurs de $f$ pour ces points). On obtient la valeur de $f_{xy}(x,y)$ pour le point cible. (On peut également le faire dans la direction opposée, calculer en premier $f_{y}$ et ensuite $f_{x}$ sur ces valeurs. Les deux résultats sont équivalents.)

Aux frontières de l'ensemble de points à traiter, il manque certains des points environnants pour calculer les dérivées. Les points manquants peuvent être estimés par un certain nombre de méthodes. Une méthode simple et courante consiste à supposer que la pente du point existant au point cible inexistant est constante, et d'utiliser cela pour calculer une valeur hypothétique pour le point manquant.

Algorithme de convolution bicubique

L'interpolation par spline bicubique nécessite la résolution du système linéaire décrit ci-dessus pour chaque case de la grille de valeurs connues. On peut obtenir un interpolateur avec des propriétés similaires, en appliquant une convolution avec le noyau suivant dans chaque dimension :

$W(x)={\begin{cases}(a+2)|x|^{3}-(a+3)|x|^{2}+1&{\text{si }}|x|\leq 1\\a|x|^{3}-5a|x|^{2}+8a|x|-4a&{\text{si }}1<|x|<2\\0&{\text{sinon}}\end{cases}}$

où $a$ est généralement fixé à -0,5 ou -0,75. Notez que $W(0)=1$ et $W(n)=0$ pour tous les entiers non nuls $n$.

Cette approche a été proposée par Keys, qui a montré que $a=-0,5$ (ce qui correspond une spline cubique d'Hermite) produit une convergence du troisième ordre par rapport à la fonction d'origine.

Si nous utilisons la notation matricielle pour le cas commun $a=-0,5$, nous pouvons exprimer l'équation d'une manière plus conviviale : $p(t)={\tfrac {1}{2}}{\begin{bmatrix}1&t&t^{2}&t^{3}\\\end{bmatrix}}{\begin{bmatrix}0&2&0&0\\-1&0&1&0\\2&-5&4&-1\\-1&3&-3&1\\\end{bmatrix}}{\begin{bmatrix}a_{-1}\\a_{0}\\a_{1}\\a_{2}\\\end{bmatrix}}$

pour $t$ entre $0$ et $1$ pour une dimension.

Pour deux dimensions, appliqué d'abord en $X$ puis en $Y$ :

$\textstyle b_{-1}=p(t_{x},a_{(-1,-1)},a_{(0,-1)},a_{(1,-1)},a_{(2,-1)})$

$\textstyle b_{0}=p(t_{x},a_{(-1,0)},a_{(0,0)},a_{(1,0)},a_{(2,0)})$

$\textstyle b_{1}=p(t_{x},a_{(-1,1)},a_{(0,1)},a_{(1,1)},a_{(2,1)})$

$\textstyle b_{2}=p(t_{x},a_{(-1,2)},a_{(0,2)},a_{(1,2)},a_{(2,2)})$

$\textstyle p(x,y)=p(t_{y},b_{-1},b_{0},b_{1},b_{2})$

Utilisation en infographie

L'algorithme bicubique est fréquemment utilisé pour la mise à l'échelle d'images et de vidéos pour l'affichage (voir Redimensionnement d'image). Il préserve les détails fins mieux que l'algorithme bilinéaire.

Toutefois, en raison des lobes négatifs sur le noyau de convolution, l'algorithme provoque un dépassement (halo). Cela peut causer la saturation du signal, c'est donc un artefact (voir également les effets d'anneau), mais cela augmente le piqué d'image (la netteté apparente), et peut être souhaitable.