Image réciproque

En mathématiques, l'image réciproque — ou la préimage — d'une partie B d'un ensemble Y par une application f : X → Y est le sous-ensemble de X constitué des éléments dont l'image par f appartient à B : $f^{-1}(B)=\{x\in X\mid f(x)\in B\}$. Elle est donc caractérisée par :

Représentation de l'image réciproque $f^{-1}(B)$ de B par une fonction f (qui ici est injective mais non surjective).

$x\in f^{-1}(B)\Leftrightarrow f(x)\in B$.

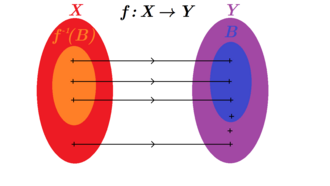
Exemples

• L'image réciproque $f^{-1}(\{y\})$ d'un singleton $\{y\}$ par une fonction f est l'ensemble des antécédents de y par f.
• Considérons l'application f : {1, 2, 3} → {a, b, c, d} définie par f(1) = a, f(2) = c, f(3) = d. L'image réciproque de {a, b} par f est f⁻¹({a, b}) = {1}.

L'application « image réciproque »

Avec cette définition, f⁻¹ est l'application « image réciproque (par f) », dont l'ensemble de définition est l'ensemble des parties de Y et dont l'ensemble d'arrivée est l'ensemble des parties de X.

Mise en garde : lorsque f est une bijection, il ne faut pas confondre cette application sur les parties avec la bijection réciproque de f, également notée f⁻¹, de Y dans X. L'image réciproque par f s'identifie avec l'image directe par cette bijection réciproque f⁻¹. Pour éviter toute confusion, Birkhoff et Mac Lane parlent d'une « application d'ensembles » qu'ils notent f_* au lieu de f⁻¹.

Propriétés élémentaires

• Pour toutes parties $B_{1}$ et $B_{2}$ de $Y$ :

  $f^{-1}\left(B_{1}\cup B_{2}\right)=f^{-1}(B_{1})\cup f^{-1}(B_{2})$ ;

  $f^{-1}\left(B_{1}\cap B_{2}\right)=f^{-1}(B_{1})\cap f^{-1}(B_{2})$ ;

  $f^{-1}\left(B_{1}\setminus B_{2}\right)=f^{-1}(B_{1})\setminus f^{-1}(B_{2})$.

• Pour toute partie $B$ de $Y$, $f(f^{-1}(B))=B\cap \mathrm {Im} (f)$.
  • En particulier, si $f$ est surjective alors $f(f^{-1}(B))=B$.

    On peut même prouver que $f$ est surjective si et seulement si pour toute partie $B$ de $Y$ on a $f(f^{-1}(B))=B$.

• Pour toute partie $A$ de $X$, $A\subset f^{-1}(f(A))$.

  L'inclusion dans l'autre sens est fausse en général si $f$ n'est pas injective.

  On peut même prouver que $f$ est injective si et seulement si pour toute partie $A$ de $X$ on a $f^{-1}(f(A))=A$.

• Pour toute famille $\left(B_{i}\right)_{i\in I}$ de parties de $Y$ :

  $f^{-1}\left(\bigcap _{i\in I}B_{i}\right)=\bigcap _{i\in I}f^{-1}(B_{i})$ ;

  $f^{-1}\left(\bigcup _{i\in I}B_{i}\right)=\bigcup _{i\in I}f^{-1}(B_{i})$.

• Si l'on considère de plus une application $g:Y\rightarrow Z$, alors l'image réciproque d'une partie $C$ de $Z$ par la composée $g\circ f$ est :

  $(g\circ f)^{-1}\left(C\right)=f^{-1}(g^{-1}(C))$.

Articles connexes

• Relation binaire réciproque
• L'opération d'image réciproque en géométrie différentielle, aussi appelée « tiré en arrière » ou « pullback ».