Gyrobicoupole octogonale allongée
En géométrie, la gyrobicoupole octogonale allongée est un des 92 solides de Johnson, nommés et décrits par Norman Johnson en 1966 (ce solide est noté J37 dans sa classification). Comme son nom l'indique, il peut être construit en allongeant une gyrobicoupole octogonale (J29) et en insérant un prisme octogonal entre ses deux moitiés. Le solide résultant est localement de sommet régulier — l'arrangement des quatre faces incidentes sur un sommet quelconque est le même pour tous les sommets; ceci est unique parmi les solides de Johnson. Néanmoins, il n'est pas semi-régulier, et par conséquent pas un solide d'Archimède, puisqu'il existe des paires de sommets tels qu'il n'y a pas d'isométrie du solide qui applique l'une vers une autre. Essentiellement, deux types de sommets peuvent être distingués par leurs "voisins de voisins". Une autre manière de voir que le polyèdre n'est pas de sommet régulier est de noter qu'il existe exactement une ceinture de huit carrés autour de son équateur, qui distingue les sommets sur la ceinture des sommets de chaque côté.
| Gyrobicoupole octogonale allongée | |

| |
| Type | Gyrobicoupole allongée J36 - J37 - J38 |
|---|---|
| Sommets | 24 |
| Arêtes | 48 |
| Faces | (nombre : 26) 8 t 18 c |
| Configuration faciale | 24 de 3.43 |
| Groupe symétrique | D4d |
| Dual | - |
| Propriétés | convexe |
| modifier |
|
Le solide peut être aussi vu comme le résultat de la torsion d'une des coupoles octogonales (J4) sur un rhombicuboctaèdre (un solide d'Archimède) de 45 degrés. Sa similarité avec le rhombicuboctaèdre lui donne les noms alternatifs de pseudorhombicuboctaèdre ou gyro-rhombicuboctaèdre[1].
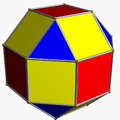 Rhombicuboctaèdre |
 Éclatement avant rotation |
 Pseudorhombicuboctaèdre |
Références
modifier- ↑ Robert Ferréol, « Rhombicuboctaèdre », sur mathcurve.com (consulté le )