Pavage en moulin à vent
Le pavage en moulin à vent (en anglais : pinwheel tiling) est un exemple de pavage fractal.
Cet article ne cite pas suffisamment ses sources ().
Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ».
En pratique : Quelles sources sont attendues ? Comment ajouter mes sources ?
Histoire
modifier
Les pavages Pinwheel sont des pavages apériodiques définis par Charles Radin et basés sur une construction faite par John Conway. Il s'agit du premier exemple connu de tuile qui peut paver le plan mais uniquement de façon complexe, en le sens suivant : tout pavage admissible fait apparaître la tuile dans une infinité d'orientations différentes.
Usages
modifier
La Federation Square, un complexe de bâtiments à Melbourne, est basée sur le pavage Pinwheel. Dans le projet, le modèle du pavage est utilisé pour créer la sous-structure d'encadrement pour les façades ce qui permet que les façades soient fabriquées en dehors du site, dans une usine, puis qu'elles soient érigées pour former les façades. Le système de pavage Pinwheel était fondé sur un triangle composé en zinc, zinc perforé, grès ou en verre (connu comme une tuile), qui rejoint 4 autres tuiles semblables sur un cadre en aluminium, pour former un "panel".
Cinq panneaux ont été fixés à un châssis en acier galvanisé, formant un "méga-panel", qui a été ensuite hissé sur des cadres de support pour la façade. Le positionnement par rotation des carreaux sur les façades donne aux façades un style aléatoire et incertain d'une composition de qualité, même si son processus de construction est basé sur de la préfabrication et de la répétition.
Construction
modifierDescription
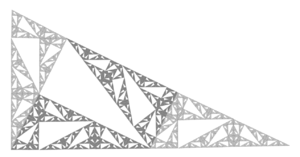
modifierSoit T le triangle droit de côté 1, 2 et d'hypoténuse √5. Conway a compris que T peut être divisé en 5 copies isométriques de son image par une homothétie de coefficient 1/√5 à l'aide de mises à l'échelle, de translations et de rotations adéquates. Cette opération peut être répétée pour obtenir une suite infinie de triangles tous copies isométriques de T. L'union de tous ces triangles donne un pavage constitué par des copies isométriques de T.
Dans ce pavage, des copies isométriques apparaissent dans une infinité d’orientations (cela est dû aux angles arctan(1/2) et arctan(2) de T, tous deux non commensurables avec π). En dépit de cela, tous les sommets ont des coordonnées rationnelles.
Le triangle T en position initiale est appelé triangle standard quand ses côtés ont pour coordonnées (-0,5 ; -0,5), (0,5 ; -0,5), (-0,5 ; 1,5). Si on multiplie ce triangle standard par la matrice , il peut être divisé en 5 triangles Pinwheel de la taille initiale. Ceci est appelé la règle agrandir et subdiviser, ou encore, la règle de substitution Pinwheel.[réf. souhaitée]
Voir aussi
modifierBibliographie
modifier- (en) Michael Whittaker, « The fractal dual of the pinwheel tiling », (conférence en 29 diapos)
- (en) Michael Baake, Dirk Frettlöh et Uwe Grimm, « Pinwheel patterns and powder diffraction », Philos. Mag., vol. 87, nos 18-21, , p. 2831-2838 (lire en ligne)
- (en) Natalie Priebe Frank et Michael F. Whittaker, « A fractal version of the pinwheel tiling », Math. Intell., vol. 33, no 2, , p. 7-17 (DOI 10.1007/s00283-011-9212-9), arXiv:1001.2203
Articles connexes
modifierLiens externes
modifier- Pinwheel sur le site "Tilings Encyclopedia"
- Implémentation : version « nue » et version avec du CSS+HTML
