Formule d'Euler
La formule d'Euler est une égalité mathématique, attribuée au mathématicien suisse Leonhard Euler. Elle s'écrit, pour tout nombre réel x,
et se généralise aux x complexes.
Ici, le nombre e est la base des logarithmes naturels, i est l'unité imaginaire, sin et cos sont des fonctions trigonométriques.
Description
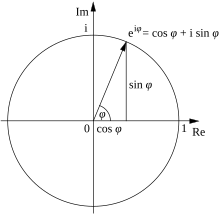
modifierCette formule peut être interprétée en disant que la fonction x ↦ eix, appelée fonction cis[1], décrit le cercle unité dans le plan complexe lorsque x varie dans l'ensemble des nombres réels.
x représente la mesure (en radians) de l'angle orienté que fait la demi-droite d'extrémité l'origine et passant par un point du cercle unité avec la demi-droite des réels positifs. La formule n'est valable que si sin et cos ont des arguments exprimés en radians plutôt qu'en degrés.
La démonstration est fondée sur les développements en série entière de la fonction exponentielle z ↦ ez de la variable complexe z et des fonctions sin et cos considérées à variables réelles.
En fait, la même démonstration montre que la formule d'Euler est encore valable pour tous les nombres complexes x.
La formule établit un puissant lien entre l'analyse et la trigonométrie. Selon Richard Feynman, c'est « l'une des formules les plus remarquables […] de toutes les mathématiques[2]. » Elle est utilisée pour représenter les nombres complexes sous forme trigonométrique et permet la définition du logarithme pour les arguments complexes. En utilisant les propriétés de l'exponentielle
et
(qui sont aussi valables pour tous les nombres complexes a, b et pour tout entier k), il devient facile de dériver plusieurs identités trigonométriques ou d'en déduire la formule de Moivre. La formule d'Euler permet une interprétation des fonctions cosinus et sinus comme combinaisons linéaires de fonctions exponentielles :
Ces formules (aussi appelées formules d'Euler) constituent la définition moderne des fonctions et (y compris lorsque x est une variable complexe)[3] et sont équivalentes[4] à la formule d'Euler (appliquée à x et à –x), qui devient alors une tautologie.
Dans les équations différentielles, la fonction x ↦ eix, est souvent utilisée pour simplifier les dérivations, même si le problème est de déterminer les solutions réelles exprimées à l'aide de sinus et cosinus. L'identité d'Euler est une conséquence immédiate de la formule d'Euler.
En électrotechnique et dans d'autres domaines, les signaux qui varient périodiquement en fonction du temps sont souvent décrits par des combinaisons linéaires des fonctions sinus et cosinus (voir analyse de Fourier), et ces dernières sont plus commodément exprimées comme parties réelles de fonctions exponentielles avec des exposants imaginaires, en utilisant la formule d'Euler.
Démonstrations
modifierPar les séries de Taylor
modifierLe développement en série de la fonction exp de la variable réelle t peut s'écrire :
et s'étend à tout nombre complexe t : le développement en série de Taylor reste absolument convergent et définit l'exponentielle complexe.
En particulier pour t = ix avec x réel :
Cette série peut être séparée en deux en regroupant les termes pairs et impairs. En effet, un réarrangement de l'ordre des termes de la série est possible ici, car il s'agit d'une série absolument convergente, autrement dit d'une famille sommable. On obtient alors, en utilisant le fait que :
On voit ainsi apparaître les développements en série de Taylor des fonctions cosinus et sinus[5] :
ce qui, en remplaçant dans l'expression précédente de eix, donne bien :
Par le calcul différentiel
modifierPour tout nombre complexe k, la seule application f : ℝ → ℂ vérifiant f ' = kf et f(0) = 1 est l'application x ↦ exp(kx) (la démonstration est identique à celle pour k réel, donnée dans l'article détaillé).
L'application f définie par vérifie
Elle coïncide donc avec l'application x ↦ exp(ix).
Historique
modifierLa formule d'Euler fut mise en évidence pour la première fois par Roger Cotes en 1714 sous la forme ln(cos x + i sin x) = ix (où ln désigne le logarithme népérien, c'est-à-dire le logarithme de base e)[6],[7]. Ce fut Euler qui publia la formule sous sa forme actuelle en 1748, en basant sa démonstration sur la formule de Moivre et à l'aide d'équivalents et de passages à la limite[8],[9]. Aucun des deux mathématiciens ne donna une interprétation géométrique de la formule : l'interprétation des nombres complexes comme des affixes de points d'un plan ne fut vraiment évoquée que cinquante années plus tard (voir Caspar Wessel).
Applications
modifier- La formule d'Euler permet d'affirmer que la détermination principale du logarithme complexe de est , pour tout .
- Un exemple d'application en électromagnétisme est le courant alternatif : puisque la différence de potentiel d'un tel circuit oscille, elle peut être représentée par un nombre complexe : Afin d'obtenir une quantité mesurable, on prend la partie réelle[10] :
- La linéarisation, qui repose sur la formule d'Euler et la formule du binôme de Newton, transforme tout polynôme en cos(x) et sin(x) en une combinaison linéaire de divers cos(nx) et sin(nx), ce qui rend alors immédiat le calcul de ses primitives.
Voir aussi
modifierArticles connexes
modifier- Théorème de Descartes-Euler
- Relation d'Euler dans le triangle
- Méthode d'Euler, calcul approché d'équations différentielles et de primitives
- Identité d'Euler : eiπ + 1 = 0
Références
modifier- (en) Alan Sultan et Alice F. Artzt, The mathematics that every secondary school math teacher needs to know, Studies in Mathematical Thinking and Learning, Taylor & Francis, 2010, p. 326.
- (en) Richard P. Feynman, Robert B. Leighton et Matthew Sands (en), Feynman Lectures on Physics [détail de l’édition], vol. 1, p. 22, d'après (en) « Euler's identity » sur Wikiquote.
- Srishti D. Chatterji, Cours d'analyse, vol. 2 : Analyse complexe, PPUR, (lire en ligne), p. 96.
- Chatterji 1997, p. 97.
- Ernst Hairer et Gerhard Wanner, L'Analyse au fil de l'histoire, Springer, , p. 59
- Dominique Flament, Histoire des nombres complexes : Entre algèbre et géométrie, Paris, CNRS Éditions, (ISBN 2 271 06128 8), p. 80.
- (en) John Stillwell, Mathematics and Its History [détail des éditions], p. 294.
- L. Euler, Introduction à l'analyse infinitésimale, article 138.
- Flament 2003, p. 83-84.
- Voir des exemples dans : Electromagnetism (2e édition), I.S. Grant, W.R. Phillips, Manchester Physics Series, 2008 (ISBN 0-471-92712-0).

