Forme d'une goutte de pluie

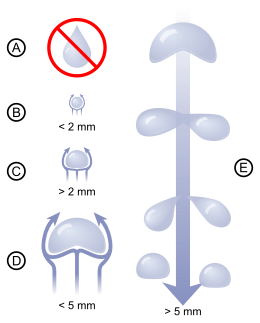
L'article goutte montre que si la plupart du temps, les gouttes d'eau dans l'air, par exemple, sont sphériques (brouillard, bruine et petites pluies), elles peuvent également prendre des formes très diverses : sphériques, disque incurvé comme un globule rouge, parachute avec bourrelet.

Dynamiques de la formation des gouttes de pluies.

Analyse physique

La forme de la goutte est déterminée par un équilibre entre la tension superficielle qui tend à conserver une forme sphérique et la résistance de l'air (ou traînée aérodynamique). Cette dernière dépend de la vitesse de chute de la goutte. Prédire la forme de la goutte consiste à déterminer sa vitesse et la traînée aérodynamique puis à en déduire sa déformation.

La goutte, initialement sphérique de rayon $R$, chute sous l'effet de son poids $\rho _{\rm {liq}}\,{\frac {4}{3}}\pi R^{3}g$ et est ralentie par la traînée aérodynamique.

Sous l'effet de la traînée aérodynamique, la goutte se déforme. Une variation de courbure $C$ d'une extrémité à l'autre de la goutte, du fait de la tension superficielle correspond à un écart de pression $\Delta p=\gamma \,C$ (cf Pression de Laplace).

La Grandeur sans dimension pertinente dans ce problème est le nombre de Weber qui compare les effets inertiels aux effets de tension de surface.

Accélération et vitesse terminale

Dans le référentiel de l'air, l'accélération de la goutte résulte d'une part de son poids (la poussée d'Archimède due à l'air est ici négligée), d'autre part de la traînée aérodynamique.

Valeur du $C_{x}$ de la sphère à tous les Reynolds possibles.

Pour cette traînée aérodynamique, on peut utiliser la formulation inertielle, propre aux hauts nombre de Reynolds. Cette formulation inertielle utilise le $C_{x}$ bien connu dont la valeur dans toute la plage des Reynolds possibles dessine la courbe rouge du graphe ci-contre.

On peut donc écrire :

${\frac {4}{3}}\pi R^{3}\rho _{\rm {liq}}\,{\frac {{\rm {d}}V}{{\rm {d}}t}}={\frac {4}{3}}\pi R^{3}\rho _{\rm {liq}}\,g-{\frac {1}{2}}\rho _{\rm {air}}\,V^{2}\,\pi R^{2}C_{x}$

Autrement dit :

$\rho _{\rm {liq}}\,R^{3}\,\left({\frac {4}{3}}\pi g-{\frac {4}{3}}\pi {\frac {{\rm {d}}V}{{\rm {d}}t}}\right)={\frac {1}{2}}\rho _{\rm {air}}\,V^{2}\,\pi R^{2}C_{x}$

Le $C_{x}$ présent dans cette équation peut être pris, en ordre de grandeur, comme unitaire (voir la courbe rouge ci-contre).

Après simplifications, on gagne à présenter la précédente égalité sous la forme suivante :

${\frac {{\rm {d}}V}{{\rm {d}}t}}+{\bigg [}{\frac {\rho _{\rm {air}}}{\rho _{\rm {liq}}}}\ {\frac {3}{8R}}\ C_{x}{\bigg ]}\ V^{2}=g$

En effet, on peut y reconnaître l'équation différentielle classique :

$V'+a\ V^{2}=g$

la variable de $V$ et $V'$étant bien sûr le temps $t$, $a$ représentant le contenu des grands crochets et $g$ toujours l'accélération de la pesanteur.

Pour intégrer cette équation différentielle, il faut s'assurer que le contenu $a$ des grands crochets est une constante. Ce sera le cas si le $C_{x}$ est pris comme constant. Au demeurant, il est facile de comprendre que, quel que soit le $C_{x}$ (variable) éprouvé par la goutte lors de son accélération dans l'air, sa vitesse terminale finira par être fonction de son $C_{x}$ terminal (c.-à-d. le $C_{x}$ correspondant à cette vitesse terminale, ou plus exactement au Reynolds à cette vitesse terminale). Il n'y a donc pas d'objection à l'intégration.

La solution de l'intégration de l'équation différentielle ci-dessus est, classiquement :

$V={\frac {{\sqrt {g}}\;Tanh(a\ {\sqrt {g}}\ t)}{\sqrt {a}}}$

du moins si l'on fait usage de la condition initiale $V(t=0)=0$

Cette intrusion de la fonction tangente hyperbolique est habituelle dans les calculs de balistique.

Par chance, pour le temps très grand auquel la goutte va connaître sa vitesse de chute stabilisée $V_{\infty }$, la fonction $Tanh$ tend vers l'unité. On dégage donc :

$V_{\infty }={\sqrt {\frac {g}{a}}}$

soit :

$V_{\infty }={\sqrt {\frac {g}{{\bigg [}{\frac {\rho _{\rm {air}}}{\rho _{\rm {liq}}}}\ {\frac {3}{4D}}\ C_{x}{\bigg ]}}}}$

du moins si l'on utilise préférentiellement le diamètre D de la sphère. Ce qui peut s'écrire encore :

$V_{\infty }={\sqrt {{\frac {\rho _{\rm {liq}}}{\rho _{\rm {air}}}}{\frac {4\ g\ D}{3\ C_{x}}}}}$

Observation de ce résultat

Vitesse et Reynolds gouttes d'eau dans l'air selon leur diamètre, Beard & Pruppacher

Vitesse des gouttes d'eau de diamètre < 1 mm.

Animation de la déformation des gouttes de pluie selon leur diamètre

• Dans leur ouvrage essentiel, Clift, Grace et Weber proposent le même libellé pour la vitesse terminale des sphères rigides (si l'on néglige également la Poussée d'Archimède de l'air sur la goutte).

Les mêmes auteurs notent qu'entre les Reynolds 750 et 350 000 le $Cx$ de sphères rigides se montre à peu près constant et égal à $0,445$ mais cette plage de Reynolds est justement celle où les gouttes perdent progressivement leur forme sphérique (ce que l'on observe ci-contre à gauche sur le graphe du $C_{x}$ de la sphère en fonction du diamètre au fait que la courbe du $C_{x}$ diverge de la courbe fuchsia réservée aux sphères lisses).

Voir aussi à gauche l'animation montrant la déformation des gouttes de pluie (les cercles rouges représentent les sphères équivalentes aux gouttes).

• À l'observation de ce résultat, on peut être tenté de penser que la vitesse terminale $V_{\infty }$ est fonction de la racine carrée du diamètre, alors que les graphes de Beard et Pruppacher (ci-contre à droite) indiquent une vitesse terminale évoluant linéairement avec le diamètre (au moins pour les diamètres inférieurs à 1 mm). La raison de ce paradoxe apparent est que le $C_{x}$ n'est pas constant mais, au contraire, variable avec le diamètre et le Reynolds, comme l'indique le graphe ci-dessus à gauche ainsi que le grand graphe du Cx de la sphère selon le Reynolds.

• Tous les calculs ci-dessus ont été faits en utilisant comme diamètre des gouttes le diamètre de la sphère équivalente, c.-à-d. le diamètre de la sphère de même volume que la goutte. C'est une habitude chez les physiciens-météorologues puisqu'ils sont confrontés à des gouttes dont la forme n'est pas forcément sphérique (au moins pour les plus grosses)(c'est d'ailleurs ce qui explique que sur le graphe du Cx de la sphère aux différents Reynolds, la courbe "brouillard et pluie" diverge de la courbe rouge des sphères rigides). Il faut d'ailleurs ajouter que le $C_{x}$ utilisé dans ces mêmes calculs et dans les différents graphes est établi en référence à la surface frontale de la sphère de même volume que la goutte ; de même, le Reynolds est construit en référence au diamètre de cette sphère de même volume.

• Avec ce libellé de la vitesse de chute stabilisée (ou vitesse terminale), on peut calculer la Traînée $\textstyle {\frac {1}{2}}\rho _{\rm {air}}V_{\infty }^{2}\ (\pi R^{2})\ C_{x}$ : on trouve alors comme libellé de cette traînée le poids de la goutte.

Éclatement d'une grosse goutte de pluie.

• Quand le rayon $R$ est fort, la vitesse $V_{\infty }$ est aussi plus forte. Inversement, cela explique que dans la nature, les très petites gouttes de liquide (comme celles créant le brouillard) chutent avec une vitesse très faible alors que les grosses gouttes de pluie chutent avec une forte vitesse : Lorsque les gouttes de pluie atteignent un diamètre de 5,5 à 6 mm, leur vitesse est si forte que les efforts aérodynamiques les font éclater ; ceci explique qu'il n'existe pas de goutte de pluie de diamètre supérieur à 5,5 ou 6 mm (animation ci-contre).

• Pour une masse volumique $\rho _{\rm {air}}$ plus forte, la vitesse terminale $V_{\infty }$ est plus faible. Inversement, dans le vide (pour $\rho _{\rm {air}}=0$) , une goutte acquerrait une vitesse quasi infinie (du moins si la goutte ne s'évaporait pas immédiatement).
• Quand le $C_{x}$ de la goutte est plus fort (goutte déformée, par exemple), la $V_{\infty }$ est plus faible : le $C_{x}$ a donc bien un rôle de freinage...

Gravité subjective et forme

Dans le référentiel de la goutte, l'accélération de la gravité est diminuée de l'accélération propre de la goutte. L'écart correspondant de pression hydrostatique d'une extrémité à l'autre de la goutte vaut donc :

$\Delta p=\rho _{\rm {liq}}\,\left(g-{\frac {{\rm {d}}V}{{\rm {d}}t}}\right)\,R$

À cause de la pression de Laplace, cet écart de pression correspond à un écart de courbure, comme il a été dit ($\Delta p=\gamma \,C$).

Forme et vitesse

Des équations ci-dessus, il résulte que tout au cours du temps :

$\gamma \,C=\rho _{\rm {air}}\,V^{2}$

Cette équation donne la déformation de la goutte par compétition entre les effets de tension superficielle et les effets de frottement dans l'air. Ainsi, une forte déformation de la goutte est atteinte lorsque $C\simeq 1/R$. En réalité, cela est vrai uniquement en l'absence d'oscillations de la goutte, comme nous verrons plus loin.

Dans le régime de chute libre, lorsque la goutte a atteint son régime de vitesse terminale, cette équation se réécrit :

$\gamma \,C=\rho _{\rm {liquide}}\,R\,g$

Si on considère que la goutte est déformée à partir du moment où la courbure est de l'ordre de $1/R$, cela donne une taille caractéristique de la goutte en dessous de laquelle elle reste sphérique :

$R_{c}={\sqrt {\frac {\gamma }{\rho g}}}$ Cette longueur est, un peu fortuitement, la longueur capillaire.

Éclatement des grosses gouttes de pluie.

Par conséquent, une goutte de pluie qui fait moins de 3 mm de diamètre (longueur capillaire de l'eau) aura une forme complètement sphérique. Une goutte plus grosse pourra prendre une forme plus étrange (cacahuète, parachute ou sac à bourrelet...)(animation ci-contre). Dans ce dernier cas, l'air qui s'engouffre à l'intérieur du sac fait bientôt éclater la goutte en une multitude de gouttelettes de taille inférieure à 3 mm.

Collision avec le sol ou un objet

Quand la goutte touche le sol ou une surface horizontale, elle s’aplatit et éventuellement éclate ou rebondit en créant de minuscules gouttes d'aérosols, facilement inhalées et qui seraient responsables de l'odeur développée par certaines pluies et éventuellement de la libération de virus et bactéries à partir du sol ou de l'air.

Voir aussi

Bibliographie

• É. Reyssat, F. Chevy, A.-L. Biance, L. Petitjean and D. Quéré, "Shape and instability of free-falling liquid globules", EPL, 80, 34005 (2007)

Articles connexes

• Goutte (physique)
• Distribution des gouttes de pluie
• Capteur de gouttelettes
• Pluie
• Molécule d'eau