Famille de Petersen
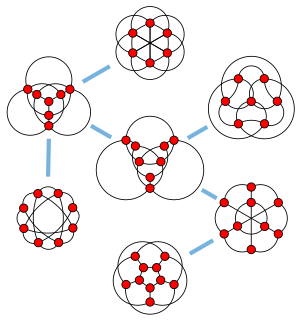
En mathématiques, et plus précisément en théorie des graphes, la famille de Petersen est un ensemble de sept graphes non orientés contenant le graphe de Petersen et le graphe complet K6. Cette famille a été découverte et étudiée par le mathématicien danois Julius Petersen.
Définition
modifierLa forme des transformations Δ-Y et Y-Δ utilisée pour définir la famille de Petersen est la suivante :
- Si un graphe G contient un sommet s ayant exactement trois voisins (donc trois arêtes partant de lui), la transformation Y-Δ de G en s est le graphe obtenu en supprimant s (et les trois arêtes qui en partent) de G et en ajoutant une nouvelle arête entre chaque couple de voisins de s.
- Si un graphe H contient un triangle rst, la transformation Δ-Y de H en rst est le graphe formé en supprimant les arêtes rs, st, et rt de H, et en ajoutant un nouveau sommet x et les trois arêtes rx, sx et tx.
(le nom de ces transformations provient de la forme en Δ d'un triangle du graphe, et de la forme en Y d'un sommet de degré 3). Bien que ces opérations puissent en principe conduire à des multigraphes, cela ne se produit pas pour les graphes de la famille de Petersen. Ces transformations conservant le nombre d'arêtes d'un graphe, on ne peut, en les utilisant, construire qu'un nombre fini de graphes (ou de multigraphes) à partir d'un graphe initial donné.
La famille de Petersen est définie comme l'ensemble des graphes qui peuvent être atteint à partir du graphe de Petersen par combinaison de transformations Δ-Y et Y-Δ. Parmi les sept graphes de la famille, outre le graphe de Petersen, on trouve le graphe complet K6 à six sommets, le graphe à huit sommets obtenu en supprimant une arête du graphe biparti complet K4,4, et le graphe complet triparti à sept sommets K3,3,1.
Mineurs exclus
modifierUn mineur d'un graphe G est un autre graphe formé à partir de G en contractant et en supprimant des arêtes. Le théorème de Robertson-Seymour montre que de nombreuses familles de graphes peuvent être caractérisées par un ensemble fini de mineurs exclus : ainsi, d'après le théorème de Wagner, les graphes planaires sont ceux n'ayant comme mineurs ni le graphe complet K5, ni le graphe biparti complet K3,3.
Neil Robertson, Paul Seymour et Robin Thomas utilisèrent la famille de Petersen pour caractériser de même les graphes plongeables dans l'espace usuel sans entrelacements, définis comme étant les plongements tels que tout cycle du graphe soit la frontière d'un disque non traversé par le reste du graphe[1]. Horst Sachs avait déjà étudié ces plongements, montré que les sept graphes de la famille de Petersen ne pouvaient être ainsi plongés, et posé la question de caractériser les graphes plongeables sans entrelacements par une famille de mineurs exclus[2]. Robertson et al. résolurent cette question en montrant que la famille de Petersen constituait exactement l'ensemble des mineurs exclus recherché.
La famille de Petersen est aussi contenue dans l'ensemble des mineurs exclus pour une autre famille de graphes fermée pour les mineurs, la famille des graphes YΔY-réductibles. Un graphe connexe est YΔY-réductible s'il peut être réduit à un seul sommet par une succession de transformations Δ-Y ou Y-Δ, de suppressions de boucles ou d'arêtes multiples, de suppression de sommets n'ayant qu'un voisin, et de remplacements d'un sommet ayant exactement deux voisins par une arête les reliant. Ainsi, le graphe complet K4 peut être réduit à un seul sommet par la séquence : la transformation Y-Δ qui en fait un triangle à côtés doubles, la suppression de ces trois côtés doubles, la transformation Δ-Y l'amenant au graphe en Y K1,3, et la suppression des trois sommets simples. Chacun des graphes de la famille de Petersen est un mineur exclus minimal pour la famille des graphes YΔY-réductibles[3].
Cependant, Neil Robertson a donné un exemple, montré ci-contre, d'un graphe apical (en) (un graphe obtenu en ajoutant un sommet à un graphe planaire, et donc clairement plongeable sans entrelacements) qui n'est pas YΔY-réductible, montrant que les graphes YΔY-réductibles forment un sous-ensembles strict des graphes plongeables sans entrelacements, et donc possèdent un ensemble de mineurs exclus plus vaste que la famille de Petersen[3]. En fait, Yaming Yu a montré en 2006 qu'il y avait au moins 68 897 913 652 mineurs exclus pour cette famille[4].
Notes
modifier- Cette définition est plus forte que celle correspondant à la version usuelle, demandant que deux cycles quelconques soient non entrelacés, puisqu'elle exclut également les entrelacs brunniens ; voir Robertson, Seymour et Thomas 1993.
- (en) Horst Sachs, « On a spatial analogue of Kuratowski's Theorem on planar graphs – an open problem », dans M. Horowiecki, J. W. Kennedy et M. M. Sysło, Graph Theory: Proceedings of a Conference held in Łagów, Poland, February 10–13, 1981, vol. 1018, Springer-Verlag, , p. 230–241.
- (en) Klaus Truemper, Matroid Decomposition, Academic Press, , 100–101 p. (lire en ligne).
- (en) Yaming Yu, « More forbidden minors for wye-delta-wye reducibility », Electronic Journal of Combinatorics, vol. 13, no 1, , #R7 (lire en ligne).
Références
modifier- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Petersen family » (voir la liste des auteurs).
- (en) Neil Robertson, P. D. Seymour et Robin Thomas, « Linkless embeddings of graphs in 3-space », Bulletin of the American Mathematical Society, vol. 28, no 1, , p. 84–89 (MR 1164063, arXiv math/9301216, lire en ligne).