Effet Yarkovsky

L’effet Yarkovsky est la conséquence du rayonnement thermique reçu par un astéroïde sur son déplacement.

Effet Yarkovsky
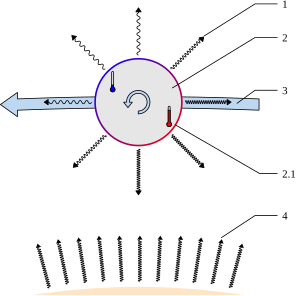
1. Radiation de la surface de l'astéroïde
2. Rotation de l'astéroïde
3. Orbite de l'astéroïde
4. Radiation du soleil

Les astéroïdes concernés ont un diamètre inférieur à environ 20 km, et ceux de la ceinture principale peuvent être mis en résonance, et regroupés en objets géocroiseurs^[Quoi ?].

Notations

Soient les notations suivantes concernant l'astéroïde :

• R : rayon moyen ;
• D : diamètre moyen ;
• E : obliquité de l'axe de rotation ;
• ω : vitesse angulaire, ou « pulsation », de la rotation ;
• P : période de rotation ;
  • ω = 2π/P
• κ : conductivité thermique ;
• ρ : masse volumique ;
• C_p : chaleur spécifique à pression constante ;
• T : température de surface ;
• A : albédo de Bond ;
• m : masse ;
• S : surface ;
• ε : émissivité thermique de la surface ;

ainsi que les constantes physiques suivantes :

• c : vitesse de la lumière ;
• σ : constante de Stefan-Boltzmann.

Généralités

Fig. 1 – Schéma des composantes de la force résultante de l'effet Yarkovsky. C'est la composante le long de la trajectoire qui est responsable du changement du demi-grand axe de l'orbite de l'astéroïde.

Lors de la révolution d'un astéroïde autour du Soleil, un côté va être plus illuminé que l'autre (et donc recevra plus de photons). Son insolation est donc asymétrique. Il faudra alors un certain temps τ pour réémettre ces photons, pendant lequel l'astéroïde va tourner sur lui-même. Il en résulte donc une force opposée à sa direction de réémission (voir Fig. 3, et la pression de radiation). L'effet Yarkovsky est donc la force qui résulte de cette réémission du photon : c'est un effet différé dans le temps, contrairement à la pression de radiation classique.

Cette force peut se décomposer, selon l'axe porté par la droite passant par le Soleil et l'astéroïde, et la droite qui lui est perpendiculaire (voir Fig. 1). C'est la composante le long de la trajectoire qui a pour effet une augmentation séculaire du demi-grand axe pour un sens de rotation prograde de l'astéroïde, et une diminution pour un sens rétrograde. Cette force modifie aussi l'excentricité et l'inclinaison de l'orbite, et la vitesse de rotation de l'astéroïde.

L'effet Yarkovsky dépend des variables et paramètres suivants :

• distance au Soleil,
• inclinaison de l'axe de rotation,
• taille de l'astéroïde (diamètre moyen D),
• forme de l'astéroïde,
• propriétés thermiques, et en particulier l'inertie thermique,
• vitesse angulaire de rotation ω .

On distingue deux effets Yarkovsky différents (voir Fig. 2) :

1. l'effet diurne, qui se caractérise par :
   • l'axe de rotation perpendiculaire au plan orbital,
   • une échelle de temps de l'inertie thermique de l'ordre de la période de rotation,
   • une dépendance du sens de rotation ;
2. l'effet saisonnier, qui se caractérise par :
   • l'axe de rotation dans le plan orbital,
   • une échelle de temps de l'inertie thermique de l'ordre de la période de révolution,
   • une indépendance du sens de rotation, ce qui a pour effet de circulariser les orbites.

Brève théorie

Il y a deux étapes dans le calcul de la force Yarkovsky [Bottke Jr. et al., 2002] :

1. détermination de la distribution de température à la surface,
2. évaluation de la force de recul due à la radiation thermique.

Température de surface

Pour déterminer la distribution de température à la surface de l'astéroïde, on doit prendre en compte l'inertie thermique de celui-ci, la vitesse de rotation, et la diffusion de chaleur. Cette dernière est trop complexe pour pouvoir la traiter analytiquement sans simplification. On la linéarise donc, ce qui revient à considérer des petites variations de chaleur [Vokrouhlicky, 1999].

Fig. 3 - L'effet Yarkovsky diurne. Un photon incident frappe la surface de l'astéroïde (en rouge), puis est réémis après un certain temps τ (caractéristique de l'inertie thermique) perpendiculairement à la surface (voir pression de radiation) de l'astéroïde (en vert). En moyenne (sur la surface ensoleillé) la force sera donc orientée d'un angle dα(τ) par rapport à la direction d'incidence des photons (en magenta).

Pour des astéroïdes de forme complexe et/ou de paramètres thermiques hétérogènes, le calcul nécessite un traitement plus sophistiqué pour éviter des calculs trop gourmands en temps. Ainsi, on déterminera la température de surface en utilisant le flux d'énergie à l'intérieur de l'astéroïde :

${\vec {\nabla }}\cdot (\kappa \ {\vec {\nabla }}T)=\rho \ C_{p}{\frac {\partial T}{\partial t}}$,

et la condition limite à la surface de l'astéroïde :

$(\kappa \ {\vec {\nabla }}T\cdot {\vec {n}}_{\perp })+\varepsilon \ \sigma \ T^{4}=\alpha \ E$ .

La dernière équation se réfère à un élément de surface orientée par le vecteur unitaire ${\vec {n}}_{\perp }$ ; E est le flux solaire à travers cette surface, et $\alpha \ =1-A$. Cette équation est une condition limite pour la détermination de la température T mais requiert la connaissance de la forme et l'état de rotation de l'astéroïde par le biais de E, ce qui implique de longs temps de calcul.

Dans le cas de petites variations thermiques, on peut dire que la température T autour du corps est proche de T₀ (c'est-à-dire $T=T_{0}+\Delta T$, la variation de température étant petite devant T₀ : $\delta ={\frac {\Delta T}{T_{0}}}\ll 1$). Si T₀ est constant, ces deux équations peuvent être réécrites pour la variable δ, tandis qu'on peut écrire le terme de température de la dernière équation comme suit [Vokrouhlicky, 1998] :

$T^{4}\sim T_{0}^{4}\ (1+4\delta +\ldots )$.

Évaluation de la force

L'astéroïde conserve presque toujours une asymétrie dans son irradiation (à l'exception des très petits corps de moins de 10 centimètres de diamètre, qui sont gardés isothermes par une conduction de chaleur interne efficace). Il en résulte donc une direction privilégiée vers laquelle la force va agir [Vokrouhlicky et al., 2005].

À ce stade, il parait utile de mettre en évidence quelques grandeurs caractéristiques. Pour un terme de Fourier donné à la fréquence ν de la décomposition de E, deux paramètres fondamentaux apparaissent [Vokrouhlicky et al., 2000 ; Bottke Jr. et al., 2002] :

• la profondeur de pénétration de l'onde thermique dans l'astéroïde : $l_{\nu }={\sqrt {\frac {\kappa }{\rho \ C_{p}\ \nu }}}$,
• le paramètre thermique $\Theta _{\nu }={\frac {\sqrt {\kappa \ \rho \ C_{p}\ \nu }}{\varepsilon \sigma T_{\star }^{3}}}$, qui permet de mesurer la relaxation entre l'absorption et la réémission à la fréquence ν d'un photon, T_* étant la température subsolaire définie comme $\varepsilon \sigma T_{\star }^{4}=\alpha E_{\star }$, où $E_{\star }$ est le flux de radiation solaire à la distance de l'astéroïde.

Pour les astéroïdes qui viennent de la ceinture principale, on pourra considérer une excentricité e petite, ce qui permet de linéariser le terme δ. Enfin, on supposera une émission isotropique des photons, ce qui correspond à la loi de Lambert.

Avec toutes les simplifications précédentes, on obtient l'expression de la force due à l'effet Yarkovsky suivante :

${\mathbf {f} }=-\ {\frac {2}{3}}\ {\frac {\varepsilon \sigma }{mc}}\int _{S}dS(u,v)\ T^{4}\ {\mathbf {n} }_{\perp }$,

où f est la force par unité de masse, et (u, v) les coordonnées de l'élément de surface.

Si on adopte un système local de coordonnées avec z selon l'axe de rotation de l'astéroïde et x, y dans le plan équatorial, on différencie alors deux variantes de ${\vec {f}}$ :

• l'effet diurne : f_x, f_y dépendent de la fréquence de rotation ω ,
• l'effet saisonnier : f_z dépend uniquement de ν_mm = 2π/P, la fréquence de mouvement moyen.

Dans un formalisme plus complet (c'est-à-dire sans linéarisation de la température), les deux effets sont couplés.

Ces forces agissent sur le demi-grand axe de l'orbite de l'astéroïde. En moyennant ces petites perturbations sur une révolution, on a :

$\left({\frac {{\rm {d}}a}{{\rm {d}}t}}\right)_{\rm {diurne}}=-\ {\frac {8\alpha }{9}}\ {\frac {\phi }{\nu _{mm}}}\ F_{\omega }(R',\Theta _{\omega })\cos \epsilon \ +\ {\mathcal {O}}(e)$,

$\left({\frac {{\rm {d}}a}{{\rm {d}}t}}\right)_{\rm {saisonnier}}={\frac {4\alpha }{9}}\ {\frac {\phi }{\nu _{mm}}}\ F_{\nu _{mm}}(R',\Theta _{\nu _{mm}})\sin ^{2}\epsilon \ +\ {\mathcal {O}}(e)$,

où $\phi =\pi R^{2}{\mathcal {E}}_{0}/(mc)$ est le coefficient de pression de radiation, $R'=R/l_{\nu }$ une longueur normalisée, et $F_{\nu }$ la fonction définie comme suit:

$F_{\nu }(R',\Theta )=-\ {\frac {K_{1}(R')\ \Theta _{\nu }}{1+2K_{2}(R')\ \Theta _{\nu }+K_{3}(R')\ \Theta _{\nu }^{2}}}$.

Les paramètres $K_{i}(R')$ sont des fonctions analytiques de $R'$. La dernière équation est la même pour les deux effets Yarkovsky, en remplaçant $\nu =\omega$ pour l'effet diurne, et $\nu =\nu _{\rm {mm}}$ pour l'effet saisonnier. On peut remarquer que le paramètre $\Theta _{\nu }$ est le paramètre qui fait la plus grande différence entre les deux effets.

Les paramètres importants dans le changement du demi-grand axe par l'effet Yarkovsky sont donc :

• l'obliquité et la rotation : l'effet saisonnier produit toujours une diminution de a et est maximum à $\epsilon =90^{\circ }$, alors que l'effet diurne peut produire une augmentation ($\epsilon <90^{\circ }$) et une diminution ($\epsilon >90^{\circ }$) de a, et est maximum pour $\epsilon =0^{\circ }$. De plus, l'effet Yarkovsky est négligeable dans la limite des rotations à vitesse infinie ou nulle car les variations de température sont nulles le long d'une même longitude.
• la taille : l'effet Yarkovsky est négligeable pour les très petits astéroïdes car l'onde thermique chauffe de la même manière toute sa surface (donc typiquement quand D est de l'ordre de $l_{\nu }$), et pour les grands objets car la gravitation l'emporte (à partir de D égal à 20 kilomètres).
• conductivité thermique : pour les corps très poreux ou ayant une surface semblable au régolithe, κ est très faible (de l'ordre de 10^-3 W·m^-1·lK^-1). Pour les corps rocheux (chondrites ou glace), κ est intermédiaire (1 W m⁻¹ K⁻¹), alors que pour les corps ferreux κ est très élevé (40 W m⁻¹ K⁻¹). Les variations de κ modifient les paramètres $l_{\nu }$ et $\Theta _{\nu }$ : un κ petit implique que $l_{\nu }\approx 0$, et donc ${\dot {a}}\approx \Theta$ et l'effet Yarkovsky disparaît ; un κ grand implique que $R'\rightarrow 0$ et $l_{\nu }\rightarrow \infty$, et donc ${\dot {a}}\approx {\frac {R'^{2}}{\Theta }}$, ce qui correspond à un équilibre thermique de l'astéroïde.
• distance au Soleil : l'effet Yarkovsky diminue quand la distance de l'astéroïde au Soleil augmente.

Les valeurs caractéristiques de changement du demi-grand axe sont de l'ordre de 0,1 unité astronomique pour les objets sub-kilométriques, et d'environ 0,01 ua pour les objets de diamètre supérieur au kilomètre^[Quoi ?]. Par ailleurs, le paramètre κ a de moins en moins d'importance au fur et à mesure que la taille de l'astéroïde augmente.

Ainsi, l'effet Yarkovsky est le premier mécanisme pour les astéroïdes ayant un diamètre inférieur à 20 kilomètres qui leur permette d'échapper à la ceinture principale et est susceptible de les amener sur des orbites de type géocroiseur.

Outre le changement du demi-grand axe, qui est l'effet le plus important et le plus prononcé de l'effet Yarkovsky, celui-ci se traduit aussi par des changements de l'excentricité et l'inclinaison de l'orbite de l'astéroïde.

Étude de l'effet Yarkovsky

L'étude de l'effet Yarkovsky est l'un des objectifs de la mission OSIRIS-REx de la NASA. À partir de la fin de l'année 2018, la sonde OSIRIS-REx orbitera autour de l'astéroïde Bénou, un astéroïde géocroiseur, pour en étudier avec plus de précision l'effet Yarkovsky afin de mieux déterminer la trajectoire de ce corps céleste. Cet effet avait déjà, au préalable, été étudié sur cet astéroïde à l'aide de télescopes terrestres et spatiaux montrant que son orbite s'était décalée de 160 km depuis sa découverte en 1999.

Voir aussi

Bibliographie

• (en) [Bottke Jr. et al., 2002] W.F. Bottke Jr., D. Vokrouhlicky (de), D.P. Rubincam et M. Broz (2002). The effect of Yarkovsky thermal forces on the dynamical evolution of asteroids and meteoroids, in Asteroids III (W.F. Bottke Jr. et al., eds.), p. 395–408. Univ. of Arizona, (Tucson). « Bibliographic Code: 2002aste.conf..395B », sur ADS.
• (en) [Vokrouhlicky, 1998] D. Vokrouhlicky (1998). Diurnal Yarkovsky effect as asource of mobility of meter-sized asteroidal fragments. Astronomy & Astrophysics, vol. 335, p. 1093–1100. « Bibliographic Code: 1998A&A...335.1093V », sur ADS.
• (en) [Vokrouhlicky, 1999] D. Vokrouhlicky (1999). A complete linear model for the Yarkovsky thermal force on spherical asteroid fragments. Astronomy & Astrophysics, vol. 344, p. 362–366. « Bibliographic Code: 1999A&A...344..362V », sur ADS.
• (en) [Vokrouhlicky et al., 2000] D. Vokrouhlicky, A. Milani et S.R. Chesley (2000). Yarkovsky effect on small near-Earth asteroids : mathematical formulation and examples. Icarus, vol. 148, p. 118–138. « Bibliographic Code: 2000Icar..148..118V », sur ADS DOI 10.1006/icar.2000.6469.
• (en) [Vokrouhlicky et al., 2005] D. Vokrouhlicky, M. Broz, W.F. Bottke, D. Nesvorny et A. Morbidelli (2005). Non-gravitational perturbations and evolution of the asteroid main belt, in Dynamics of Populations of Planetary Systems (Z. Knezevic et A. Milani, eds.), n^o 197 in Proceedings IAU Colloquium, p. 145–156. International Astronomical Union, Cambridge Academic Press, (Cambridge). « Bibliographic Code: 2005dpps.conf..145V », sur ADS DOI 10.1017/S1743921304008609.

Articles connexes

• Effet YORP
• Effet Magnus (bien que concerné par des forces de nature très différente, il concerne aussi un changement de trajectoire liée à une rotation de l'objet en déplacement dans un fluide, donc hors vide spatial)
• Ivan Yarkovsky
• Paramètres d'accélération non gravitationnelle
• Trou de serrure gravitationnel
• Planètes mineures où l'effet Yarkovsky a été détecté

Liens externes

• « Rapport de stage sur les effets des perturbations non gravitationnelles sur l'évolution du spin des NEAs »^{(Archive.org • Wikiwix • Archive.is • Google • Que faire ?)}
• (en) Article arXiv sur l'influence de la dérive due à l'effet Yarkovsky et prédiction sur les astéroïdes géocroiseurs connus (C. R. Nugent, A. Mainzer, J. Masiero, T. Grav et J. Bauer) [PDF]
• (en) David Vokrouhlický (de) et William F. Bottke, « Yarkovsky and YORP effects », sur Scholarpedia