Wikipédia

Effet Sagnac

On appelle effet Sagnac le décalage temporel de la réception de deux signaux lumineux tournant en sens inverse autour de la circonférence d'un disque en rotation (par rapport à un référentiel inertiel), quand ils sont émis par un émetteur-récepteur fixé sur ce disque.

Schéma d'un dispositif possible.

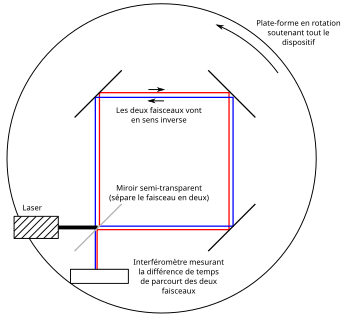
L'effet Sagnac a été découvert par Georges Sagnac en 1913[1]. En physique classique, il est interprétable comme une asymétrie de la vitesse des signaux lumineux par rapport à la circonférence du disque en rotation. En physique relativiste, l'effet correspond à l'impossibilité de synchroniser des horloges sur une courbe fermée soumise à la gravitation, ou à une accélération (en cas de rotation).

En 1925, Michelson et Gale mesurèrent la rotation de la Terre grâce à un grand interféromètre en utilisant l'effet Sagnac. Le gyroscope à fibre optique utilisé comme gyromètre est une application directe de l'effet Sagnac.

Prévision en physique classique

modifier

On appelle « effet Sagnac » le décalage temporel de la réception de signaux lumineux « tournant en sens inverse » quand ils sont émis par un émetteur-récepteur fixé sur un disque tournant. En effet, si un émetteur placé sur un disque en rotation envoie deux signaux lumineux contraints de suivre la circonférence du disque, chacun dans un sens, les deux signaux reviennent à l'émetteur après un tour complet mais avec un léger décalage temporel qui dépend de la vitesse de rotation du disque.

En physique classique, ce décalage temporel entre les instants d'arrivée des deux signaux lumineux tournant en sens inverse se calcule comme suit.

 
Les signaux lumineux partant dans des sens opposés parcourent des distances différentes avant de rencontrer à nouveau l’émetteur qui tourne avec le disque.

Le long de la circonférence d'un disque de rayon R tournant à la vitesse   (au niveau du rayon R) on fait tourner :

  • un rayon lumineux dans le même sens que le disque et, en notant t le temps qu'il met pour rencontrer à nouveau l'émetteur, l'observateur du laboratoire vérifie l'égalité  , avec  , d'où  
  • un rayon lumineux dans le sens opposé à celui du disque et, en notant t' le temps qu'il met pour rencontrer à nouveau l'émetteur, l'observateur du laboratoire vérifie l'égalité  , avec  , d'où  

Le décalage entre les arrivées des deux signaux lumineux   pour une petite vitesse de rotation.

Dans le cadre de la physique classique, ce décalage calculé dans le référentiel inertiel du laboratoire est le même que celui que l'on peut calculer dans le référentiel tournant de l'émetteur-récepteur.

Prévision en physique relativiste

modifier

En relativité, le décalage temporel calculé dans le référentiel du laboratoire n'est pas celui que l'émetteur-récepteur perçoit car il est en mouvement par rapport au laboratoire.

En utilisant la relativité générale, on trouve un décalage qui, en première approximation, est égal à celui calculé dans le référentiel du laboratoire, et ce décalage correspond à la différence de temps qui s'impose entre des horloges quand on essaie de les synchroniser le long d'un contour fermé soumis à la gravitation (ou à une accélération, due par exemple à un mouvement de rotation). Ce décalage peut aussi être interprété comme une différence entre la vitesse de la lumière dans un sens ou l'autre ; sachant que cette vitesse est toujours égale à c quand elle est mesurée en temps propre en chaque point de son parcours, mais ce temps propre ne peut être celui de l'horloge de l'émetteur-récepteur car ici les horloges ne peuvent être synchronisées avec elle[2].

Résultats expérimentaux

modifier

L'effet a d'abord été constaté et mesuré en analysant les franges d'interférences des signaux lumineux. Depuis, l'utilisation de laser, d'horloges atomiques et d'autres dispositifs, permet d'autres mesures et en particulier la mesure directe du décalage temporel.

En 1913, Sagnac a vérifié les prédictions prérelativistes de l'effet qui porte son nom en utilisant un interféromètre en rotation rapide. Il avait lui-même prédit les résultats ci-dessus dans le cadre de la physique classique. Ce fut aussi le premier résultat expérimental rapporté de ce qui fut nommé l'effet Sagnac.

En 1925, Michelson et Gale mesurèrent la rotation de la Terre grâce à un grand interféromètre.

Depuis les années soixante, des mesures de plus en plus précises ont pu être effectuées grâce à l'emploi des lasers.

Déjà, en 1914, Harzer avait constaté que l'effet subsiste en présence de la réfraction, c'est-à-dire dans un milieu où la lumière va moins vite que  .

Pour les ondes électromagnétiques, l'effet a été détecté pour les ondes radioélectriques[3] et les rayons X[3].

Pour la matière, c'est-à-dire pour les ondes de de Broglie[3] et les particules associées, l'effet a également été détecté :

Prédictions prérelativistes

modifier

L'effet Sagnac n'est pas prédictible dans le cadre de la théorie corpusculaire de la lumière d'Isaac Newton[19]. Il a été prédit, pour les ondes lumineuses, avant l'avènement de la relativité restreinte, dans le cadre de la théorie de l'éther[20]. Le physicien britannique Oliver Lodge (-) est le premier à le prévoir, dès [21],[22],[23] pour un interféromètre entraîné par la rotation de la Terre[20] puis en [21],[24] pour un interféromètre monté sur un plateau tournant[20]. Par la suite, le physicien américain Albert A. Michelson (-) en [20] puis le physicien français Georges Sagnac (-) en prévoient tous deux l'effet, toujours dans le cadre de la théorie de l'éther[20].

Prédécouverte

modifier

L'effet Sagnac est parfois dit « effet Harress-Sagnac »[25] car il s'est avéré avoir été observé pour la première fois en -[26] par Franz Harress dans une expérience de Fizeau. Harress n'a pas su expliquer les causes du déplacement des franges d'interférence qu'il observait[27]. En , l'astronome allemand Paul Harzer (-) rediscute les résultats de l'expérience de Harress et montre qu'elle met en évidence l'effet Sagnac, avec une plus grande précision que celle obtenue par Sagnac[27].

Réinterprétation relativiste

modifier

Dès , le physicien allemand Max von Laue (-) relève que la relativité restreinte prédit elle aussi l'effet[27],[28]. Par la suite, von Laue lui-même en [27],[29] — au premier ordre en v / c[27] — puis le physicien français Paul Langevin (-) en [27],[30] et en [27],[31] reprennent la démonstration de l'effet en relativité restreinte.

L'effet Sagnac est généralement considéré comme un effet de la relativité restreinte[32],[33],[3],[34],[35]. En effet, d'une part, l'effet Sagnac est un effet « purement relativiste »[36],[37] ; et, d'autre part, l'effet est « purement cinématique »[38] : il n'est pas lié à la gravitation[37],[39] ; ainsi, la relativité restreinte suffit pour prédire exactement l'effet[38] : il n'est pas nécessaire de se placer dans le cadre de la relativité générale[38].

Rotation de la Terre

modifier

L'effet Sagnac dû à la rotation de la Terre a été mesuré avec des interféromètres à ondes de matière :

  • en par Werner et al. avec des neutrons[40] ;
  • en par Lenef et al. avec des atomes de sodium (Na)[40] ;
  • en puis en par Gustavson et al. avec des atomes de césium (Cs)[40] ;
  • en par Canuel et al. avec des atomes de césium (Cs) refroidis[40].

Résultats expérimentaux récents

modifier

Au lieu de mesurer la vitesse apparente des signaux, on peut tenter de mesurer la vitesse de la lumière localement, directement, comme on le fait sans rotation.

Des expériences ont en effet été menées afin de déterminer s'il y avait une anisotropie dans un repère en rotation. En voici quelques-unes effectuées de différentes manières (sources et récepteurs en rotation ou immobiles, mesures sur un aller simple ou un aller-retour).

  • Cialdea utilise deux laser multi-modes montés sur une table en rotation et regarde les variations de leur figure d'interférence lorsque la table est mise en rotation. Il obtient une limite supérieure à l'anisotropie de 0,9 m/s.
  • Krisher utilise deux masers à hydrogène fixés au sol et séparés par un lien en fibre optique de 21 kilomètres et regarde les variations entre leur phase. Il obtient une limite supérieure à l'anisotropie de 100 m/s.
  • Champeney utilise un amortisseur de Moessbauer en rotation et un détecteur fixe pour donner une limite supérieure à l'anisotropie de 3 m/s.
  • Turner utilise une source en rotation et un détecteur de Moessbauer fixe pour donner une limite supérieure à l'anisotropie de 10 m/s.
  • Gagnon, Torr, Kolen, et Chang ont effectué un test de l'anisotropie avec un guide d'ondes. Leurs résultats négatifs sont cohérents avec la relativité restreinte.

Applications

modifier

Le gyromètre à fibre optique est une application directe de l'effet Sagnac.

Notes et références

modifier
  1. ↑ Les systèmes des savants sur Google Livres
  2. ↑ Lev Landau et Evgueni Lifchits, Physique théorique, t. 2 : Théorie des champs [détail des éditions] §89 Rotation.
  3. ↑ a b c et d Malykin et Pozdnyakova 2013, chap. 2, sec. 2.1, p. 8.
  4. ↑ a b c et d Rizzi et Ruggiero 2003, sect. 2, § 2.3, p. 184.
  5. ↑ a b et c Gautier et al. 2022, introduction, p. 1, col. 1.
  6. ↑ Gautier et al. 2022, références et notes, no 9, p. 5, col. 2.
  7. ↑ Werner et al. 1979.
  8. ↑ Atwood et al. 1984.
  9. ↑ Gautier et al. 2022, références et notes, no 10, p. 5, col. 2.
  10. ↑ Riehle et al. 1991.
  11. ↑ Gautier et al. 2022, références et notes, no 11, p. 5, col. 2.
  12. ↑ Hasselbach et Nicklaus 1993.
  13. ↑ Gautier et al. 2022, références et notes, no 12, p. 5, col. 2.
  14. ↑ Schwab et al. 1997.
  15. ↑ Gautier et al. 2022, références et notes, no 13, p. 5, col. 2.
  16. ↑ Simmonds et al. 2001.
  17. ↑ Gautier et al. 2022, références et notes, no 14, p. 5, col. 2.
  18. ↑ Wright et al. 2013.
  19. ↑ Deruelle et Uzan 2018, liv. 2, Ire part., chap. 3, sec. 3.2, p. 202.
  20. ↑ a b c d et e Gourgoulhon 2010, chap. 13, sect. 13.5, § 13.5.4, p. 465.
  21. ↑ a et b Malykin et Pozdnyakova 2013, chap. 2, sec. 2.2, § 2.2.1, p. 17.
  22. ↑ Malykin et Pozdnyakova 2013, bibliographie, no 466, p. 274.
  23. ↑ Lodge 1893.
  24. ↑ Malykin et Pozdnyakova 2013, bibliographie, no 465, p. 274.
  25. ↑ Darrigol 2014, sec. 7, § 7.9, p. 824.
  26. ↑ Darrigol 2014, sec. 7, § 7.7, p. 823.
  27. ↑ a b c d e f et g Gourgoulhon 2010, chap. 13, sect. 13.5, § 13.5.4, p. 466.
  28. ↑ Laue 1911.
  29. ↑ Laue 1920.
  30. ↑ Langevin 1921.
  31. ↑ Langevin 1937.
  32. ↑ Bhadra, Ghose et Raychaudhuri 2022, sec. 1, p. 1, col. 2.
  33. ↑ Malykin 2000, sec. 1, p. 1229, col. 2.
  34. ↑ Pascoli 2017, sec. 3, p. 567.
  35. ↑ Tartaglia et Ruggiero 2015, résumé, p. 427.
  36. ↑ Gourgoulhon 2024, préf., p. 5.
  37. ↑ a et b Spagnou 2024, chap. 4, sec. 4.1, p. 88.
  38. ↑ a b et c Spagnou 2024, chap. 4, sec. 4.2, p. 89.
  39. ↑ Spagnou 2024, chap. 4, sec. 4.1, p. 89.
  40. ↑ a b c et d Gourgoulhon 2010, chap. 13, sect. 13.5, § 13.5.6, p. 468.

Voir aussi

modifier

Articles connexes

modifier

Liens externes

modifier

Bibliographie

modifier
Ouvrages généraux
  • Jean Hladik, Pierre-Emmanuel Hladik, Le calcul tensoriel en physique, 3e édition Dunod. (ISBN 2100040715), (ISBN 2225846537), (ISBN 2225841446)
  • V. Ougarov, Théorie de la Relativité Restreinte, Deuxième Edition, Editions Mir, Moscou. Traduction française Editions Mir, 1979.
  • Edgard Elbaz, Relativité Générale et Gravitation, Editions Ellipses-Marketing, 1986, (ISBN 2729886516) (épuisé)
  • Charles W.Misner, Kip S. Thorne et John Archibald Wheeler, Gravitation, W.H. Freeman and Company, New York. (ISBN 0716703440)
Autres sources

Manuels d'enseignement supérieur

modifier

Publications historiques

modifier
Oliver Lodge
modifier
Georges Sagnac
modifier
Max von Laue
modifier
Paul Langevin
modifier

Expériences

modifier
  • [Atwood et al. 1984] (en) D. K. Atwood, M. A. Horne, C. G. Shull et J. Arthur, « Neutron phase shift in a rotating two-crystal interferometer », Phys. Rev. Lett., vol. 52, no 19,‎ , p. 1673 (DOI 10.1103/PhysRevLett.52.1673, résumé).
  • [Hasselbach et Nicklaus 1993] (en) Franz Hasselbach et Marc Nicklaus, « Sagnac experiment with electrons : observation of the rotational phase shift of electron waves in vacuum », Phys. Rev. A, vol. 48, no 1,‎ , p. 143 (DOI 10.1103/PhysRevA.48.143, résumé).
  • [Riehle et al. 1991] (en) F. Riehle, Th. Kisters, A. Witte, J. Helmcke et Ch. J. Bordé, « Optical Ramsey spectroscopy in a rotating frame : Sagnac effect in a matter-wave interferometer », Phys. Rev. Lett., vol. 67, no 2,‎ , p. 177 (DOI 10.1103/PhysRevLett.67.177, résumé).
  • [Schwab et al. 1997] (en) Keith Schwab, Niels Bruckner et Richard E. Packard, « Detection of the Earth's rotation using superfluid phase coherence », Nature, vol. 386,‎ , p. 585-587 (DOI 10.1038/386585a0, résumé).
  • [Simmonds et al. 2001] (en) R. W. Simmonds, A. Marchenkov, E. Hoskinson, J. C. Davis et R. E. Packard, « Quantum interference of superfluid 3He », Nature, vol. 412,‎ , p. 55-58 (DOI 10.1038/35083518, résumé).
  • [Werner et al. 1979] (en) S. A. Werner, J.-L. Staudenmann et R. Colella, « Effect of Earth's rotation on the quantum mechanical phase of the neutron », Phys. Rev. Lett., vol. 42, no 17,‎ , p. 1103 (DOI 10.1103/PhysRevLett.42.1103, résumé).
  • [Wright et al. 2013] (en) K. C. Wright, R. B. Blakestad, C. J. Lobb, W. D. Phillips et G. K. Campbell, « Driving phase slips in a superfluid atom circuit with a rotating weak link », Phys. Rev. Lett., vol. 110, no 2,‎ , article no 025302 (DOI 10.1103/PhysRevLett.110.025302, résumé).
Ce document provient de « https://fr.wiki.x.io/w/index.php?title=Effet_Sagnac&oldid=218883026 ».