Deltoïde (courbe)
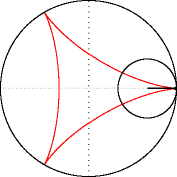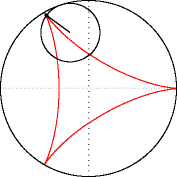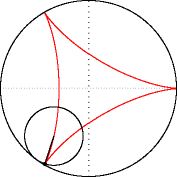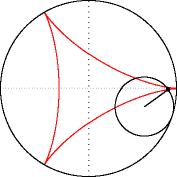
La deltoïde n'est autre qu'une hypocycloïde à trois rebroussements. Sa forme ressemble un peu à celle de la lettre grecque delta majuscule, d'où son nom. Cet exemple de roulette fut étudié pour la première fois par Leonhard Euler en 1745.
Équations paramétriques
modifierEn écrivant la position du point d'un cercle de rayon roulant sans glisser à l'intérieur d'un cercle de rayon , on obtient l'équation paramétrique suivante :
L'équation cartésienne est de la forme :
ce qui montre que cette courbe est algébrique de degré 4. Elle possède trois points singuliers (les trois points de rebroussement), et elle est de genre zéro.
Propriétés géométriques
modifier- La longueur du deltoïde est 16a[1]. L'aire du domaine délimité par le deltoïde est .
- Une règle dont les deux extrémités sont astreintes à glisser sur la deltoïde vient tangenter la deltoïde en un troisième point : le point de tangence décrit deux fois la deltoïde lorsque les extrémités ne la décrivent qu'une fois.
- L'enveloppe des droites de Simson d'un triangle est une deltoïde (on l’appelle deltoïde de Steiner, ce théorème étant dû à Jakob Steiner).
- La développante de la deltoïde a pour équation cartésienne
- Elle présente un point double à l'origine, ce que l'on peut vérifier en opérant une rotation imaginaire y → iy, qui aboutit à l'équation :
- courbe qui présente un point double à l'origine dans .
Bibliographie
modifier- Jacques Hadamard, « On the three-cusped hypocycloid », The Mathematical Gazette, vol. 29, , p. 66-67
Références
modifier- ↑ A. Bouvier, M. George, F. Le Lionnais, Dictionnaire des mathématiques, PUF (1979)
- ↑ (en) Jeffrey A. Boyle, « Using rolling circles to generate caustic envelopes resulting from reflected light », Amer. Math. Monthly, vol. 122, no 5, , p. 452-466 (lire en ligne)