Dérivation numérique

En analyse numérique, les algorithmes de dérivation numérique évaluent la dérivée d'une fonction mathématique ou d'un sous-programme de fonction en utilisant les valeurs de la fonction et peut-être d'autres propriétés connues sur la fonction.

Différences finies

La méthode la plus simple consiste à utiliser des approximations de différences finies.

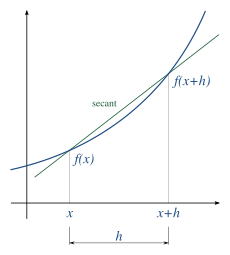
Une simple estimation à deux points consiste à calculer la pente d'une droite sécante proche passant par les points $(x, f (x))$ et $(x + h, f (x + h))$ ^[1]. On choisit un petit nombre $h$ , qui représente une petite variation autour de $x$ , qui peut être positive ou négative. La pente de cette droite est

{\frac {f(x+h)-f(x)}{h}}.

Cette expression est le quotient de différence de Newton (également connu sous le nom de différence divisée du premier ordre).

La pente de cette sécante diffère de la pente de la ligne tangente d'une quantité approximativement proportionnelle à $h$ . Lorsque $h$ tend vers zéro, la pente de la ligne sécante se rapproche de la pente de la ligne tangente. Par conséquent, la vraie dérivée de $f$ en $x$ est la limite de la valeur du quotient de différence à mesure que les lignes sécantes se rapprochent de plus en plus d'une ligne tangente :

f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}.

Puisque la substitution immédiate de 0 à $h$ donne la forme indéterminée $0 / 0$ , le calcul direct de la dérivée peut être peu intuitif.

De manière équivalente, la pente pourrait être estimée en utilisant les positions $(x - h)$ et $x$ .

Une autre formule à deux points consiste à calculer la pente d'une droite sécante proche passant par les points $(x - h, f (x - h))$ et $(x + h, f (x + h))$ . La pente de cette droite est

{\frac {f(x+h)-f(x-h)}{2h}}.

Cette formule est connue sous le nom de quotient de différence symétrique. Dans ce cas, les erreurs de premier ordre s'annulent, de sorte que la pente de ces lignes sécantes diffère de la pente de la ligne tangente d'une quantité approximativement proportionnelle à $h 2$ . Par conséquent, pour de petites valeurs de $h$ , il s'agit d'une approximation plus précise de la tangente que l'estimation unilatérale. Cependant, bien que la pente soit calculée en $x$ , la valeur de la fonction en $x$ n'est pas impliquée.

L'erreur d'estimation est donnée par

R={\frac {-f^{(3)}(c)}{6}}h^{2}

,

où $c$ est un point entre $x - h$ et $x + h$ . Cette erreur n'inclut pas l'erreur d'arrondi due aux nombres représentés et aux calculs effectués avec une précision limitée.

Le quotient de différence symétrique est utilisé comme méthode d'approximation de la dérivée dans un certain nombre de calculatrices, notamment TI-82, TI-83, TI-84, TI-85, qui utilisent toutes cette méthode avec $h$ = 0,001^[2]^,^[3].

Taille de pas

Exemple montrant la difficulté de choisir

h

en raison à la fois d'une erreur d'arrondi et d'une erreur de formule

Une considération importante dans la pratique lorsque la fonction est calculée en utilisant l'arithmétique à virgule flottante de précision finie est le choix de la taille de pas $h$ . S'il est choisi trop petit, la soustraction produira une grande erreur d'arrondi. En fait, toutes les formules aux différences finies sont mal conditionnées ^[4] et, en raison de l'annulation, produiront une valeur nulle si $h$ est suffisamment petit^[5]. S'il est choisi trop grand, le calcul de la pente de la ligne sécante sera calculé avec plus de précision, mais l'estimation de la pente de la tangente en utilisant la sécante pourrait être pire^[6].

Pour les différences centrales de base, le pas optimal est la racine cubique de l'epsilon machine^[7]. Pour la formule de dérivée numérique évaluée en $x$ et $x + h$ , un choix pour $h$ qui est petit sans produire une grande erreur d'arrondi est $\sqrt ε x$ (mais pas quand $x$ = 0), où l'epsilon machine $ε$ est typiquement de l'ordre de 2,2  × 10⁻¹⁶ pour la double précision^[8] . Une formule pour $h$ qui équilibre l'erreur d'arrondi contre l'erreur sécante pour une précision optimale est^[9]

h=2{\sqrt {\varepsilon \left|{\frac {f(x)}{f''(x)}}\right|}}

(mais pas quand $f''(x) = 0$ ), et son utilisation nécessite une connaissance de la fonction.

Pour les calculs informatiques, les problèmes sont exacerbés car, bien que $x$ contienne nécessairement un nombre à virgule flottante représentable avec une certaine précision (32 ou 64 bits, etc. ), $x + h$ ne sera presque certainement pas exactement représentable avec cette précision. Cela signifie que $x + h$ sera changé (par arrondi ou troncature) en un nombre proche représentable par machine, avec pour conséquence que $(x + h) - x$ ne sera pas égal à $h$ ; les deux évaluations de fonction ne seront pas exactement séparées par $h$ . À cet égard, puisque la plupart des fractions décimales sont des séquences récurrentes en binaire (tout comme 1/3 est en décimal), une étape apparemment ronde telle que $h$ = 0,1 ne sera pas un nombre rond en binaire ; c'est 0.000110011001100...₂ Une approche possible est la suivante :

h := sqrt(eps) * x;
xph := x + h;
dx := xph - x;
pente := (F(xph) - F(x)) / dx;

Cependant, avec les ordinateurs, les fonctions d'optimisation du compilateur peuvent ne pas tenir compte des détails de l'arithmétique informatique réelle et appliquer à la place les axiomes des mathématiques pour en déduire que dx et h sont identiques. Avec C et les langages similaires, une directive indiquant que xph est une variable volatile empêchera cela.

Autres méthodes

Méthodes d'ordre supérieur

Des méthodes d'ordre supérieur pour approcher la dérivée, ainsi que des méthodes pour des dérivées supérieures, existent.

Ci-dessous est la méthode en cinq points pour la première dérivée (stencil à cinq points dans une dimension)^[10]:

f'(x)={\frac {-f(x+2h)+8f(x+h)-8f(x-h)+f(x-2h)}{12h}}+{\frac {h^{4}}{30}}f^{(5)}(c),

où $c \in [x - 2 h, x + 2 h]$ .

Pour d'autres configurations de stencil et ordres dérivés, le calculateur de coefficients de différence finie est un outil qui peut être utilisé pour générer des méthodes d'approximation dérivées pour n'importe quel stencil avec n'importe quel ordre dérivé (à condition qu'une solution existe).

Dérivées d'ordres supérieurs

En utilisant le quotient de différence de Newton,

f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}

on peut montrer ^[11] (pour n > 0) :

f^{(n)}(x)=\lim _{h\to 0}{\frac {1}{h^{n}}}\sum _{k=0}^{n}(-1)^{k+n}{\binom {n}{k}}f(x+kh)

Méthodes à variables complexes

Les approximations classiques aux différences finies pour la différenciation numérique sont mal conditionnées. Toutefois, si $f$ est une fonction holomorphe, à valeurs réelles sur la droite réelle, qui peut être évaluée en des points du plan complexe proches de $x$ , alors il existe des méthodes stables. Par exemple^[5], la dérivée première peut être calculée par la formule de la dérivée à étapes complexes ^[12]^,^[13]^,^[14]:

f^{\prime }(x)={\frac {\Im (f(x+\mathrm {i} h))}{h}}+O(h^{2}),\quad \mathrm {i^{2}} :=-1.

La taille de pas recommandée pour obtenir des dérivées précises pour une gamme de conditions est $h$ = 10⁻²⁰⁰ ^[6]. Cette formule peut être obtenue par développement en série de Taylor :

f(x+\mathrm {i} h)=f(x)+\mathrm {i} hf^{\prime }(x)-f''(x){\frac {h^{2}}{2!}}-\mathrm {i} f^{(3)}(x){\frac {h^{3}}{3!}}+\cdots .

La formule de dérivée à pas complexe n'est valable que pour le calcul des dérivées du premier ordre. Une généralisation de ce qui précède pour le calcul des dérivés de tout ordre utilise des nombres multicomplexes, résultant en des nombres dérivés multicomplexes^[15]^,^[16]^,^[17].

f^{(n)}(x)\approx {\frac {{\mathcal {C}}_{n^{2}-1}^{(n)}(f(x+\mathrm {i} ^{(1)}h+\ldots +\mathrm {i} ^{(n)}h))}{h^{n}}}

où le $i (k)$ désignent les unités imaginaires multicomplexes ; $\mathrm {i} ^{(1)}\equiv \mathrm {i}$ . Le ${\mathcal {C}}_{k}^{(n)}$ l'opérateur extrait le $k$ -ième composante d'un nombre multicomplexe de niveau $n$ , par exemple, ${\mathcal {C}}_{0}^{(n)}$ extrait le composant réel et ${\mathcal {C}}_{n^{2}-1}^{(n)}$ extrait le dernier composant "le plus imaginaire". La méthode peut être appliquée aux dérivées mixtes, par exemple pour une dérivée du second ordre

{\frac {\partial ^{2}f(x,y)}{\partial x\,\partial y}}\approx {\frac {{\mathcal {C}}_{3}^{(2)}(f(x+\mathrm {i} ^{(1)}h,y+\mathrm {i} ^{(2)}h))}{h^{2}}}

En général, les dérivées de tout ordre peuvent être calculées à l'aide de la formule intégrale de Cauchy^[18]:

f^{(n)}(a)={\frac {n!}{2\pi \mathrm {i} }}\oint _{\gamma }{\frac {f(z)}{(z-a)^{n+1}}}\,\mathrm {d} z,

où l'intégration se fait numériquement.

L'utilisation de variables complexes pour la dérivation numérique a commencé avec Lyness et Moler en 1967^[19]. Leur algorithme est applicable aux dérivées d'ordre supérieur.

Une méthode basée sur l'inversion numérique d'une transformée de Laplace complexe a été développée par Abate et Dubner^[20]. Un algorithme pouvant être utilisé sans nécessiter de connaissances sur la méthode ou le caractère de la fonction a été développé par Fornberg^[4].

Quadrature différentielle

La quadrature différentielle est l'approximation des dérivées en utilisant des sommes pondérées de valeurs de fonction^[21]^,^[22] La quadrature différentielle présente un intérêt pratique car elle permet de calculer des dérivées à partir de données bruitées. Le nom est en analogie avec quadrature, qu'on appele aujourd'hui intégration numérique, où des sommes pondérées sont utilisées dans des méthodes telles que la méthode de Simpson ou la méthode des trapèzes. Il existe différentes méthodes pour déterminer les coefficients de pondération, par exemple l'algorithme de Savitzky-Golay. La quadrature différentielle est utilisée pour résoudre des équations aux dérivées partielles. Il existe d'autres procédés pour calculer des dérivées à partir de données bruitées^[23].

Voir aussi

Dérivation automatique – Techniques pour évaluer la dérivée d'une fonction spécifiée par un programme informatique
Stencil (analyse numérique)
Algorithme de Savitzky-Golay
Intégration numérique – Famille d'algorithmes pour trouver l'intégrale définie d'une fonction
Équation différentielle ordinaire numérique
Lissage (mathématiques)

Références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Numerical differentiation » (voir la liste des auteurs).

↑ (en) Richard L. Burden et J. Douglas Faires, Numerical Analysis, Brooks/Cole, 2000 (ISBN 0-534-38216-9).
↑ Katherine Klippert Merseth, Windows on Teaching Math: Cases of Middle and Secondary Classrooms, Teachers College Press, 2003 (ISBN 978-0-8077-4279-2, lire en ligne ), 34
↑ Tamara Lefcourt Ruby, James Sellers, Lisa Korf, Jeremy Van Horn et Mike Munn, Kaplan AP Calculus AB & BC 2015, Kaplan Publishing, 2014 (ISBN 978-1-61865-686-5), p. 299
↑ ^{a et b} (en) B Fornberg, « Numerical Differentiation of Analytic Functions », ACM Transactions on Mathematical Software (TOMS), California Institute of Technology,‎ 1981.
↑ ^{a et b} (en) William Squire et George Trapp, « Using Complex Variables To Estimate Derivatives Of Real Functions », SIAM Review, vol. 40, n^o 1,‎ 1998, p. 110-112 (DOI 10.1137/S003614459631241X)
↑ ^{a et b} (en) Joaquim R. R. A. Martins et Andrew Ning, Engineering Design Optimization, Cambridge University Press, 1^er octobre 2021 (ISBN 978-1108833417, lire en ligne)
↑ (en) Timothy Sauer, Numerical Analysis, Pearson, 2012, 248 p..
↑ Following Numerical Recipes in C, Chapter 5.7.
↑ p. 263.
↑ (en) Milton Abramowitz et Irene Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables [détail de l’édition] (lire en ligne), voir Table 25.2.
↑ George Shilov, Elementary Real and Complex Analysis
↑ Martins, Sturdza et Alonso, « The Complex-Step Derivative Approximation », ACM Transactions on Mathematical Software, vol. 29, n^o 3,‎ 2003, p. 245–262 (DOI 10.1145/838250.838251, S2CID 7022422, CiteSeer^x 10.1.1.141.8002)
↑ Differentiation With(out) a Difference by Nicholas Higham
↑ article from MathWorks blog, posted by Cleve Moler
↑ (en) « Archived copy » [archive du 9 janvier 2014] (consulté le 24 novembre 2012)
↑ (en) Lantoine, Russell et Dargent, « Using multicomplex variables for automatic computation of high-order derivatives », ACM Trans. Math. Softw., vol. 38, n^o 3,‎ 2012, p. 1–21 (DOI 10.1145/2168773.2168774, S2CID 16253562)
↑ (en) A. Verheyleweghen, « Computation of higher-order derivatives using the multi-complex step method », 2014
↑ (en) M.J. Ablowitz et A.S. Fokas, Complex variables: introduction and applications, Cambridge University Press, 2003. Voir théorème 2.6.2
↑ (en) J. N. Lyness et C. B. Moler, « Numerical differentiation of analytic functions », SIAM J. Numer. Anal., vol. 4, n^o 2,‎ 1967, p. 202–210 (DOI 10.1137/0704019, Bibcode 1967SJNA....4..202L)
↑ (en) Abate et Dubner, « A New Method for Generating Power Series Expansions of Functions », SIAM J. Numer. Anal., vol. 5, n^o 1,‎ mars 1968, p. 102–112 (DOI 10.1137/0705008, Bibcode 1968SJNA....5..102A)
↑ (en) Chang Shu, Differential Quadrature and Its Application in Engineering: Engineering Applications, Springer, 2000 (ISBN 978-1-85233-209-9).
↑ (en) Yingyan Zhang, Advanced Differential Quadrature Methods, CRC Press, 2009 (ISBN 978-1-4200-8248-7).
↑ (en) Karsten Ahnert et Markus Abel, « Numerical differentiation of experimental data: local versus global methods », Computer Physics Communications, vol. 177, n^o 10,‎ 2007, p. 764–774 (ISSN 0010-4655, DOI 10.1016/j.cpc.2007.03.009, Bibcode 2007CoPhC.177..764A)

Liens externes

Sur les autres projets Wikimedia :

Dérivation numérique, sur Wikibooks

Portail de l'analyse

[1] (en) Richard L. Burden et J. Douglas Faires, Numerical Analysis, Brooks/Cole, 2000 (ISBN 0-534-38216-9).

[Merseth2003-2] Katherine Klippert Merseth, Windows on Teaching Math: Cases of Middle and Secondary Classrooms, Teachers College Press, 2003 (ISBN 978-0-8077-4279-2, lire en ligne ), 34

[RubySellers2014-3] Tamara Lefcourt Ruby, James Sellers, Lisa Korf, Jeremy Van Horn et Mike Munn, Kaplan AP Calculus AB & BC 2015, Kaplan Publishing, 2014 (ISBN 978-1-61865-686-5), p. 299

[Fornberg1-4] {a et b} (en) B Fornberg, « Numerical Differentiation of Analytic Functions », ACM Transactions on Mathematical Software (TOMS), California Institute of Technology,‎ 1981.

[SquireTrapp1-5] {a et b} (en) William Squire et George Trapp, « Using Complex Variables To Estimate Derivatives Of Real Functions », SIAM Review, vol. 40, n^o 1,‎ 1998, p. 110-112 (DOI 10.1137/S003614459631241X)

[edo2021-6] {a et b} (en) Joaquim R. R. A. Martins et Andrew Ning, Engineering Design Optimization, Cambridge University Press, 1^er octobre 2021 (ISBN 978-1108833417, lire en ligne)

[7] (en) Timothy Sauer, Numerical Analysis, Pearson, 2012, 248 p..

[8] Following Numerical Recipes in C, Chapter 5.7.

[9] . 263.

[10] (en) Milton Abramowitz et Irene Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables [détail de l’édition] (lire en ligne), voir Table 25.2.

[11] George Shilov, Elementary Real and Complex Analysis

[12] Martins, Sturdza et Alonso, « The Complex-Step Derivative Approximation », ACM Transactions on Mathematical Software, vol. 29, n^o 3,‎ 2003, p. 245–262 (DOI 10.1145/838250.838251, S2CID 7022422, CiteSeer^x 10.1.1.141.8002)

[13] Differentiation With(out) a Difference by Nicholas Higham

[14] rticle from MathWorks blog, posted by Cleve Moler

[15] (en) « Archived copy » [archive du 9 janvier 2014] (consulté le 24 novembre 2012)

[16] (en) Lantoine, Russell et Dargent, « Using multicomplex variables for automatic computation of high-order derivatives », ACM Trans. Math. Softw., vol. 38, n^o 3,‎ 2012, p. 1–21 (DOI 10.1145/2168773.2168774, S2CID 16253562)

[17] (en) A. Verheyleweghen, « Computation of higher-order derivatives using the multi-complex step method », 2014

[18] (en) M.J. Ablowitz et A.S. Fokas, Complex variables: introduction and applications, Cambridge University Press, 2003. Voir théorème 2.6.2

[LynessMoler1-19] (en) J. N. Lyness et C. B. Moler, « Numerical differentiation of analytic functions », SIAM J. Numer. Anal., vol. 4, n^o 2,‎ 1967, p. 202–210 (DOI 10.1137/0704019, Bibcode 1967SJNA....4..202L)

[20] (en) Abate et Dubner, « A New Method for Generating Power Series Expansions of Functions », SIAM J. Numer. Anal., vol. 5, n^o 1,‎ mars 1968, p. 102–112 (DOI 10.1137/0705008, Bibcode 1968SJNA....5..102A)

[21] (en) Chang Shu, Differential Quadrature and Its Application in Engineering: Engineering Applications, Springer, 2000 (ISBN 978-1-85233-209-9).

[22] (en) Yingyan Zhang, Advanced Differential Quadrature Methods, CRC Press, 2009 (ISBN 978-1-4200-8248-7).

[23] (en) Karsten Ahnert et Markus Abel, « Numerical differentiation of experimental data: local versus global methods », Computer Physics Communications, vol. 177, n^o 10,‎ 2007, p. 764–774 (ISSN 0010-4655, DOI 10.1016/j.cpc.2007.03.009, Bibcode 2007CoPhC.177..764A)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]