Constante de Legendre

La constante de Legendre est une constante mathématique proposée par le mathématicien Adrien-Marie Legendre et qui n'a aujourd'hui plus qu'un intérêt historique.

En rouge, les 100 000 premiers termes de la suite $a_{n}=\ln(n)-{\frac {n}{\pi (n)}}$.

Legendre conjecture en 1808 une forme précise de ce qu’on appellera plus tard le théorème des nombres premiers. Il écrit : « Quoique la suite des nombres premiers soit extrêmement irrégulière, on peut cependant trouver avec une précision très satisfaisante, combien il y a de ces nombres depuis 1 jusqu’à une limite donnée x. La formule qui résout cette question est

$y={\frac {x}{\log .x-1.08366}}$

log.x étant un logarithme hyperbolique. » En d’autres termes, Legendre affirme que

$\pi (x)={\frac {x}{\log(x)-A(x)}}$

où $\lim _{x\to \infty }A(x)=1{,}08366,$ et où π(x) désigne la fonction de compte des nombres premiers inférieurs à x.

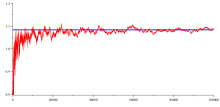
Le nombre $A:=\lim _{x\to \infty }A(x)$, qui existe, est appelé constante de Legendre. Mais sa valeur n’est pas celle supposée par Legendre.

En 1849, Tchebycheff démontre que si la limite existe, elle doit être égale à 1. Une preuve plus simple est donnée par Pintz en 1980.

C'est une conséquence immédiate du théorème des nombres premiers (qui avait été démontré en 1896 indépendamment par Jacques Hadamard et par Charles-Jean de La Vallée Poussin), sous la forme plus précise démontrée en 1899 par La Vallée Poussin

$\pi (x)={\rm {Li}}(x)+O\left(x\mathrm {e} ^{-a{\sqrt {\log x}}}\right)\quad {\text{lorsque }}x\to \infty ,$

que

$\pi (x)={\frac {x}{\log x}}+{\frac {x}{(\log x)^{2}}}+o\left({\frac {x}{(\log x)^{2}}}\right),$

et donc que A existe et vaut 1.