Problème du carré inscrit
Le problème du carré inscrit, aussi connu sous le nom de conjecture de Toeplitz, est un problème ouvert en géométrie. Ce problème s'énonce de la manière suivante:
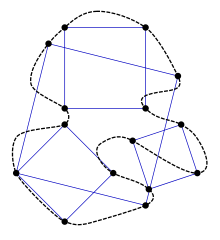
Est-ce que toute courbe fermée simple (aussi appelée courbe de Jordan) admet un carré inscrit ?
Formulé par Otto Toeplitz en 1911[1], et malgré de nombreuses avancées, ce problème est à ce jour encore irrésolu.
État des recherches
modifier- La première avancée majeure vient de Arnold Emch qui en 1913 prouve le résultat pour toute courbe convexe[2].
- En 1929, Lev Schnirelmann étend ce résultat aux courbes deux fois dérivables et telles que la dérivée seconde est continue[3]. Preuve qui fut étudiée en 1965 par Heinrich Guggenheimer qui lui ajouta et corrigea quelques points techniques[4].
- En 1950, Ogilvy publie une preuve du problème général sans aucune condition[5]. Toutefois, cette preuve se révélera fausse.
- En 1989, Walter Stromquist prouve que toute courbe localement monotone admet au moins un carré inscrit[6]. À l’exception des courbes fractales et de quelques autres courbes, toutes les courbes sont incluses dans ce théorème. Ce résultat important prouve que toute courbe que l'on pourrait tracer avec du papier et un crayon admet un carré inscrit.
Une méthode pour construire le carré inscrit d'une courbe quelconque serait :
- Approximer cette courbe par une suite de courbes localement monotones.
- Utiliser le résultat de Stromquist pour obtenir un carré inscrit à chaque itération.
- Prendre la limite de la suite des carrés.
Le seul problème avec cette méthode est que l'on ne peut garantir que le carré obtenu n'est pas dégénéré (de côté de longueur nulle).
- En 1995, Nielsen et Wright prouvent que toute courbe admettant un centre de symétrie admet au moins un carré inscrit[7]. Ceci permet de prouver la conjecture de Toeplitz pour un nombre encore plus important de courbes qui ne sont pas incluses dans le théorème de Stromquist, comme les courbes fractales symétriques. Par exemple, le flocon de Koch, qui n'est pas localement monotone mais admet un centre de symétrie, possède donc au moins un carré inscrit.
Variantes et généralisations
modifierIl a été prouvé en 1980 que toute courbe de Jordan C admet un triangle inscrit semblable à un triangle T donné[8] et une méthode existe pour le trouver. Ce résultat fut complété en 1992 en précisant que l'ensemble des sommets des triangles semblables à T et inscrits dans C est dense dans C[9].
Si au lieu d'un carré, nous considérons cette fois-ci un rectangle inscrit, le résultat a été démontré en toute généralité par Herbert Vaughan en 1977[10].
Liens externes
modifier- Un carré dans une courbe par Étienne Ghys, sur le site images des Maths
- (en) Mark J. Nielsen, Figures Inscribed in Curves. A short tour of an old problem
- (en) Igor Pak, The discrete square peg problem
- (en) Une démonstration visuelle du problème du rectangle inscrit
- (en) Quelques approches du problème sur le blog de Terence Tao
Références
modifier- Toeplitz, Oscar : Ueber einige aufgaben der analysis situs Verhandlungen der Schweizerischen Naturforschenden Gesellschaft in Solothurn, 94 (1911), p. 197.
- Emch, Arnold : Some Properties of Closed Convex Curves in a Plane. Amer. J. Math. 35 (1913), no. 4, p. 407–412.
- L. G. Shnirelman, On certain geometrical properties of closed curves (en russe) Uspehi Matem. Nauk 10, (1944) p. 34–44.
- Guggenheimer, Heinrich : Finite sets on curves and surfaces. Israel J. Math. 3 (1965) p. 104–112.
- Ogilvy, C.S. : Advanced Problems and Solutions : 4325, Amer. Math. Monthly 57 (1950), no. 6, 423–424
- Stromquist, Walter : Inscribed squares and square-like quadrilaterals in closed curves. Mathematika 36 (1989), no. 2, p. 187–197.
- Mark J. Nielsen and S.E. Wright, Rectangles inscribed in symmetric continua, Geometriae Dedicata 56: 285-297 (1995)
- Mark D. Meyerson, Equilateral triangles and continuous curves, Fund. Math. 110: 1-9 (1980).
- Mark J. Nielsen, Triangles inscribed in simple closed curves, Geometriae Dedicata 43: 291-297 (1992).
- Vaughan H., Balancing acts, Topology Proceedings. 6: 59-75 (1981) par Mark D. Meyerson