Axe orthique
L'axe orthique d'un triangle est la droite passant par les trois points d'intersection des côtés du triangle de référence et de ceux de son triangle orthique.
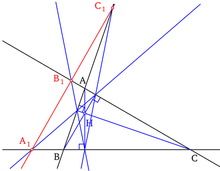
Propriétés
modifierL'équation trilinéaire de l'axe orthique est :
L'axe orthique est perpendiculaire à la droite d'Euler du triangle de référence.
Il est l'axe de l'homologie entre le triangle de référence et son triangle orthique, mais aussi de celle entre le triangle médian et le triangle tangentiel.
L'axe orthique est l'axe radical d'un faisceau de cercles comprenant le cercle circonscrit, le cercle d'Euler, le cercle orthocentroidal (le cercle tel que le segment entre l'orthocentre et le centre de gravité soit un diamètre du cercle), le cercle orthoptique de l'ellipse inscrite de Steiner, le cercle polaire et le cercle tangentiel (le cercle circonscrit au triangle tangentiel) du triangle de référence.
Liens externes
modifier(en) Eric W. Weisstein, « Orthic Axis », sur MathWorld