Arête (théorie des graphes)
En théorie des graphes, une arête, aussi appelée lien ou ligne, est une liaison entre deux sommets d'un graphe. Ces deux sommets sont les extrémités de l'arête. Une arête ayant une orientation (arête orientée) est plus souvent appelée arc ou flèche. En théorie des automates, les arcs sont appelés transitions.
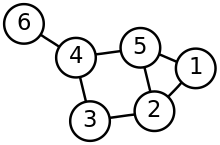
Un graphe dont toutes les arêtes sont non orientées est lui-même dit non orienté, et un graphe dont toutes les arêtes sont orientées est dit orienté ; si seulement certaines arêtes sont orientées, le graphe est dit mixte.
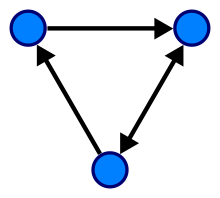
L'ensemble des arêtes d'un graphe est couramment appelé E. Un ensemble d'arcs est parfois plutôt appelé A. L'ensemble des sommets étant appelé V :
- un graphe non orienté est un couple G = (V, E) ;
- un graphe orienté est un couple G = (V, A) ;
- un graphe mixte est un triplet G = (V, E, A).
Une arête est souvent désignée par les deux sommets u et v qu'elle relie, sous la forme d'une paire {u, v} (ou un singleton {u} dans le cas d'une boucle) si elle est non orientée, ou bien un couple (u, v) si elle est orientée. Ainsi l'arête {1, 2} relie les sommets 1 et 2, et l'arc (7, 9) mène du sommet 7 au sommet 9.
Vocables associés
modifierPour une arête {u, v} ou un arc (u, v), u et v sont les sommets extrémités de l'arête. L'arête joint u et v et est incidente à u ainsi qu'à v. u et v sont dits liés, connectés, adjacents ou encore voisins. L'arête est adjacente aux autres arêtes incidentes à u ou à v. Dans le cas d'un arc, il sort de u et entre dans v, et v est consécutif à u. L'arc est consécutif aux arcs entrant dans u.
Les arêtes induisent une relation binaire (symétrique pour une arête non orientée, asymétrique pour un arc) ~ sur l'ensemble des sommets V, appelée relation d'adjacence de G : u ~ v signifie « u est adjacent à v ».
Le nombre d'arêtes |E| d'un graphe est appelé sa taille (souvent notée m). Le nombre d'arêtes incidentes à un sommet est le degré ou la valence de ce sommet, où une boucle compte double. On peut distinguer le degré sortant et le degré entrant, qui dénombrent seulement soit les arcs sortants soit les arcs entrants.
Une arête est une boucle lorsqu'elle connecte un sommet à lui-même. Une arête est parallèle à une autre arête lorsqu'elle relie les mêmes sommets (en tenant compte de l'orientation éventuelle). Un ensemble d'arêtes parallèles est une arête multiple (ou multi-arête). Un graphe est dit simple lorsqu'il ne comporte ni boucle ni arête multiple ; par opposition, on peut parler de multigraphe. Pour deux sommets u et v, un arc (u, v) et un arc (v, u) sont dits anti-parallèles l'un à l'autre.
Une arête peut avoir d'autres propriétés que ses extrémités. De nombreux algorithmes sont faits pour traiter les graphes pondérés, c'est-à-dire les graphes dans lesquelles chaque arête a un poids. Ce poids est un nombre quelconque qui peut représenter par exemple une longueur, un cout ou une capacité.
Un graphe n'ayant aucune arête est dit vide. Un graphe dont tous les sommets sont adjacents deux à deux est dit complet. Le rapport entre le nombre d'arêtes et le nombre de sommets d'un graphe est appelé sa densité : un graphe peut être creux ou contraire dense. Un graphe orienté sans multi-arcs peut avoir jusqu'à |V|2 arcs ; un graphe simple complet a en moins les boucles et les arcs anti-parallèles, donc a une taille |E| = (|V|2 − |V|)/2 = |V|(|V| − 1)/2.
Une suite d'arêtes adjacentes est une chaine ; une suite d'arcs consécutifs est appelée un chemin.
Une arête est un pont si sa suppression rompt la connexité du graphe. Un graphe est k-arête-connexe s'il est toujours connexe après la suppression de moins de k arêtes; l’arête-connexité d’un graphe est ainsi le plus grand k tel que le graphe soit k-arête-connexe.
Le complémentaire d'un graphe simple G est celui qui possède les arêtes manquantes de G, c'est-à-dire que toutes les adjacences y sont inversées par rapport à G. Le graphe transposé de G est obtenu en inversant le sens de tous les arcs de G.
Représentations
modifierEn informatique, les arêtes des graphes sont le plus souvent codées par les listes d'adjacence des sommets (c'est-à-dire, pour chaque sommet, la liste de ses voisins), ou encore par une matrice d'adjacence.
Graphe adjoint
modifierD'un graphe donné peut être déduit le graphe de ses arêtes, dit graphe adjoint ou line graph. Les sommets du graphe d'origine (dit graphe racine ou root graph) sont oubliés, et ses arêtes deviennent les sommets du nouveau graphe, en conservant leurs adjacences précédentes.
-
Graphe G
-
Le graphe adjoint L(G)
Dans le cas des graphes simples non orientés, le graphe racine peut toujours être retrouvé, sauf s'il s'agit du graphe triangle ou du graphe griffe, qui ont tous les deux le graphe triangle comme graphe adjoint. Cependant, tout graphe n'est pas un graphe adjoint : le graphe racine L-1(G) peut ne pas exister. Les graphes adjoints sont généralement très denses, car toutes les arêtes incidentes à un même sommet forment une clique dans le graphe adjoint.