Affinité (mathématiques)
En mathématiques, en particulier en géométrie, une affinité est une application linéaire ou affine, d'un espace vectoriel ou affine dans lui-même, égale à l'identité dans une direction et à une homothétie dans une autre.
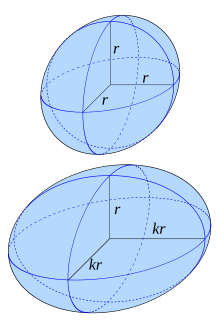
Étymologie
modifierLe terme d'affinité (affinitas en latin) dans un sens mathématique est introduit par Léonard Euler dans son ouvrage de 1748, Introductio in Analysin infinitorum[1]. Dans son chapitre De similitudine et affinitate linearum curvarum[2], Euler étudie les courbes semblables, c'est-à-dire ayant même forme avec éventuellement changement d'orientation et de taille. Ce sont les courbes images l'une de l'autre par une similitude. Après avoir remarqué qu'en multipliant les abscisses et les ordonnées par un même nombre, il transforme une courbe en une courbe semblable, il se pose la question du cas où abscisses et ordonnées sont multipliées par des nombres différents[3]. Il remarque que les courbes ne sont alors plus semblables mais, à cause d'une certaine analogie de forme, il dira qu'elles ont entre elles de l'affinité[4]. Ici, il prend le sens littéral d'affinité : entretenant un certain rapport de voisinage, de ressemblance. Ainsi, un cercle et une ellipse ne sont pas semblables mais ont entre eux de l'affinité.
L'affinité étudiée par Euler ne correspond pas stricto sensu à celle définie actuellement puisqu'il permet une modification d'échelle dans plusieurs directions, mais s'y ramène facilement par compositions d'affinités « modernes ».
Affinité vectorielle
modifierUne affinité vectorielle est un endomorphisme qui est somme directe de l'identité et d'une homothétie. Plus précisément :
Soient un espace vectoriel, et deux sous-espaces supplémentaires c.-à-d. , et un nombre réel ;
l'affinité de base ou sur , de direction , et de rapport est l'unique endomorphisme qui, restreint à , égale l'identité, et restreint à , égale l'homothétie de rapport :
si alors .
Caractérisation en dimension finie : endomorphisme diagonalisable ayant au plus deux valeurs propres distinctes, dont au plus une différente de l'unité.
Les affinités recouvrent les cas particuliers suivants:
- concernant et ,
- si , l'affinité est l'application identité ;
- si , l'affinité est l'homothétie de rapport ;
- si , l'affinité est dite hyperplane et porte le nom de dilatation ;
- concernant le rapport ,
- si , l'affinité est la projection sur parallèlement à . Si , cette affinité n'est pas bijective. C'est le seul cas où l'affinité n'est pas une transformation ;
- si , l'affinité est l'application identité. Si , c'est le seul cas où l'ensemble des invariants est différent de ;
- si , l'affinité est la symétrie par rapport à parallèlement à .
L'affinité de base , de direction , et de rapport est liée à la projection sur parallèlement à par l'égalité suivante[5]: .
Affinité ponctuelle
modifierÉtant donnés un espace affine associé à , un sous-espace affine associé à , et une direction supplémentaire de , l'affinité de base ou sur , de direction , et de rapport est l'application définie comme suit :
- pour tout point de , on construit le projeté de sur parallèlement à :
- soit l'unique sous-espace affine passant par et de direction ,
- soit l'unique point d'intersection de et de ,
- l'image de par est alors le point tel que .
Une affinité ponctuelle est nécessairement une application affine dont la partie linéaire est une affinité vectorielle.
« Réciproquement », une application affine de partie linéaire une affinité vectorielle est une affinité ponctuelle à condition d'avoir au moins un point fixe. Sans cela, on obtient une affinité glissée : composée d'une affinité ponctuelle et d'une translation de vecteur parallèle à la base de l'affinité ponctuelle.
Dans le plan euclidien, les affinités jouent un rôle dans la décomposition des transformations affines : en effet, toute transformation affine du plan euclidien se décompose en produit d'une isométrie, d'une homothétie, d'une affinité, et d'une transvection[6].
L'utilisation des affinités dans le plan permet de regrouper des courbes par familles. Par exemple :
- l'ellipse de demi grand axe et de demi petit axe est l'image d'un cercle de rayon par une affinité de base le grand axe, de direction le petit axe, et de rapport ;
- la courbe d'équation est l'image[7] de la courbe d'équation par l'affinité de base , de direction , et de rapport ;
- la courbe d'équation est l'image[7] de la courbe d'équation par l'affinité de base , de direction , et de rapport ;
- un cas particulier étonnant : l'image par l'affinité de base , de direction , et de rapport de la parabole d'équation est une parabole homothétique, contrairement au cas d'un cercle. En effet : d'après ce qui précède, l'équation de cette image est ; or l'équation de l'image[7] de par l'homothétie de rapport et de centre est , équivalente aussi à . Plus généralement toute affinité de rapport non nul transforme une parabole en une parabole semblable.
Notes et références
modifier- Serge Mehl, « Affinité », sur ChronoMath, chronologie et dictionnaire des MATHÉMATIQUES.
- La version latine est accessible sur le site Euler, page 236 et suivantes.
- En anglais, de telles modifications sont appelées anisotropic scaling.
- Leonard Euler et J. B. Labey (traducteur), Introduction à l'analyse infinitésimale, , page 236, paragraphe 442
- Dany-Jack Mercier, Cours de géométrie : préparation au CAPES et à l'agrégation, Publibooks, , page 85
- « Transformations de courbes », sur Encyclopaedia Universalis.
- L'image de la courbe d'équation par une transformation a pour équation , car .